基于EMD分解的埋弧焊电流信号分析及判断

对采集到的一组交流方波埋弧焊电流信号x（t）进行EMD分解，结果如图4-13所示。从图4-13中可以看出，EMD分解得到的IMF分量C₁、C₂、…、C₁₀对应信号从高到低不同频率成分，每个IMF分量表现信号内的真实物理信息。这样可以通过EMD分解，可方便地选取有效的IMF分量进行后续分析与处理。由于实际焊接电源工作在强干扰、高压、大电流的复杂恶劣环境中，存在功率开关管的高频切换、整流二极管的冲击、外界辐射等众多干扰因素，不仅使得焊接电源本身实际输出的电流、电压波形存在畸变，而且现场采集到的信号充满了高频噪声信号，采用EMD将信号分解成若干个IMF，对分解得到的包含高频成分的IMF进行剔除，可有效消除高频噪声信号。

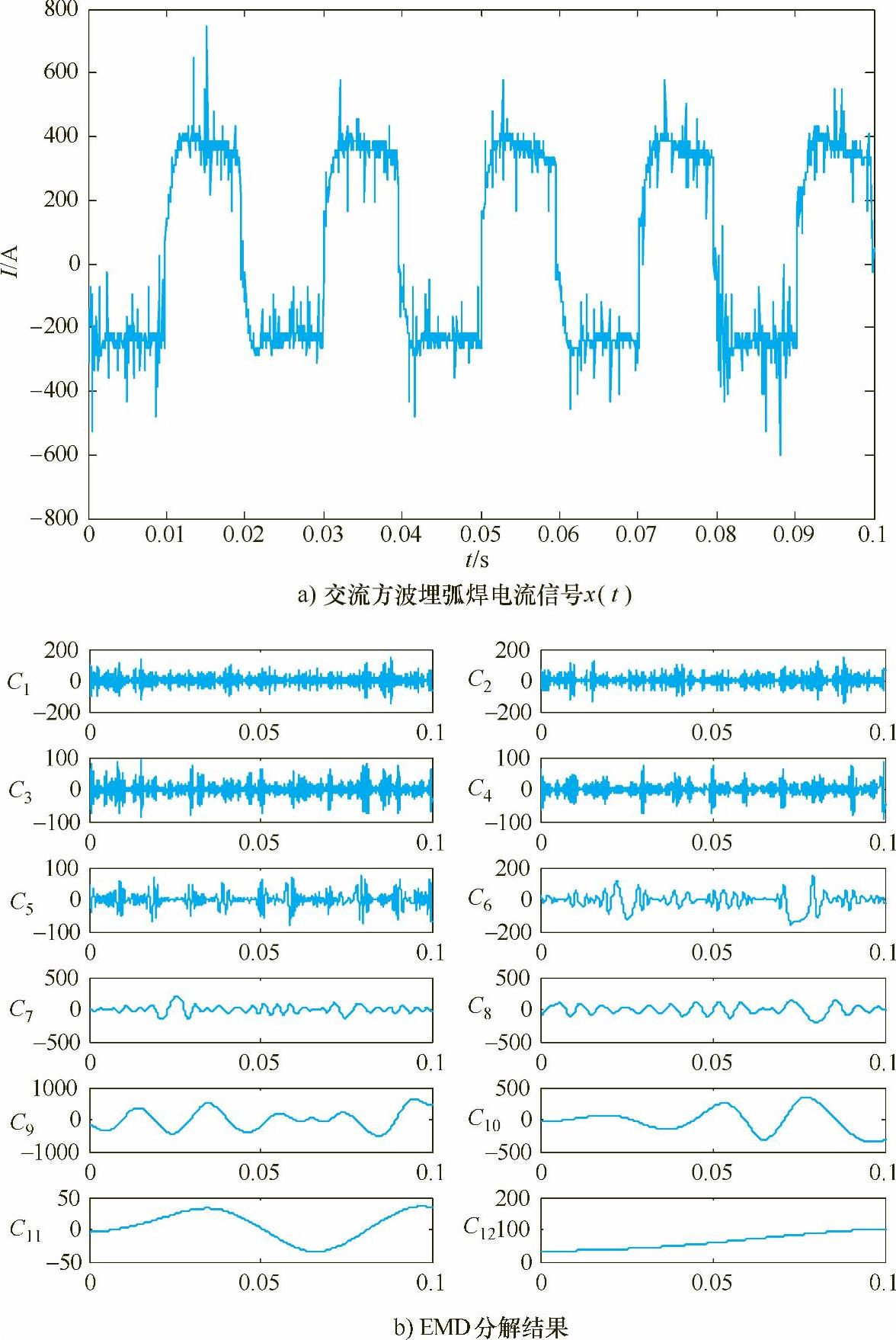
图4-13 交流方波埋弧焊电流信号及EMD分解结果

函数IMF与原始信号相关性的大小，并以各个IMF与EMD分解前信号的相关系数为判断依据，选取有效IMF集，相关系数越大，说明IMF含原信号中的有效成分越高。其相关性计算及判断准则由式（4-42）、式（4-43）组成^[23]。

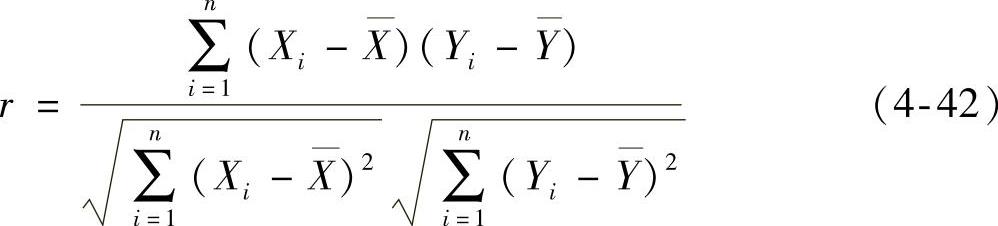
r表示变量序列X、Y的相关系数，r在-1和1之间取值。相关系数r的绝对值大小（即r），表示两个变量之间的直线相关强度；相关系数r的正负号，表示相关的方向，分别是正相关和负相关；若相关系数r=0，称零线性相关，简称零相关；相关系数r=1时，表示两个变量是完全相关。r值越大，相关程度越高。

满足选取IMF的条件为

r_i≥λ （4-43）(www.xing528.com)

式中 r_i——采集到的埋弧焊电弧能量信号EMD分解前原始信号与第i个IMF的相关系数；

λ——绝对值小于1的可选常数（通常λ<0.1时信号的相关性已经非常小，故取0.1≤λ＜1）。

表4-1为各IMF与EMD分解前信号x（t）的相关系数，取λ=0.1，即选取r_i＞0.1的IMF，选取IMF₆～IMF₁₀为有效IMF集，并进行信号重构，得到时域图如图4-14所示，不仅消除了高频噪声信号，还保留了局部畸变特征，重构后的电流波形非常清晰。

表4-1 各个IMF与信号x（t）的相关系数

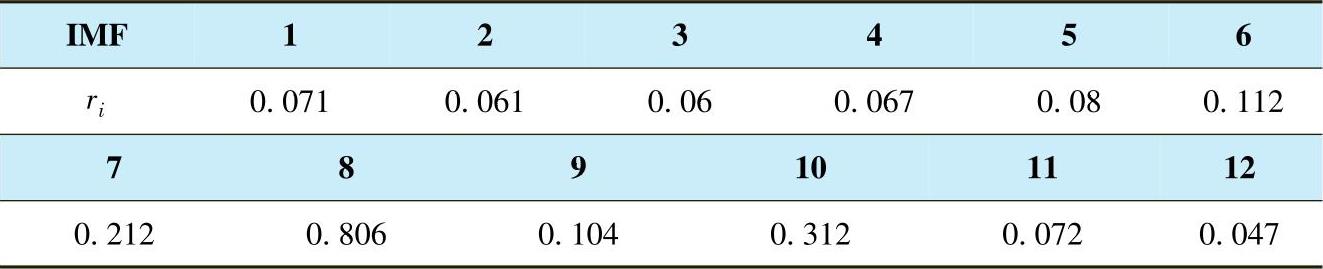
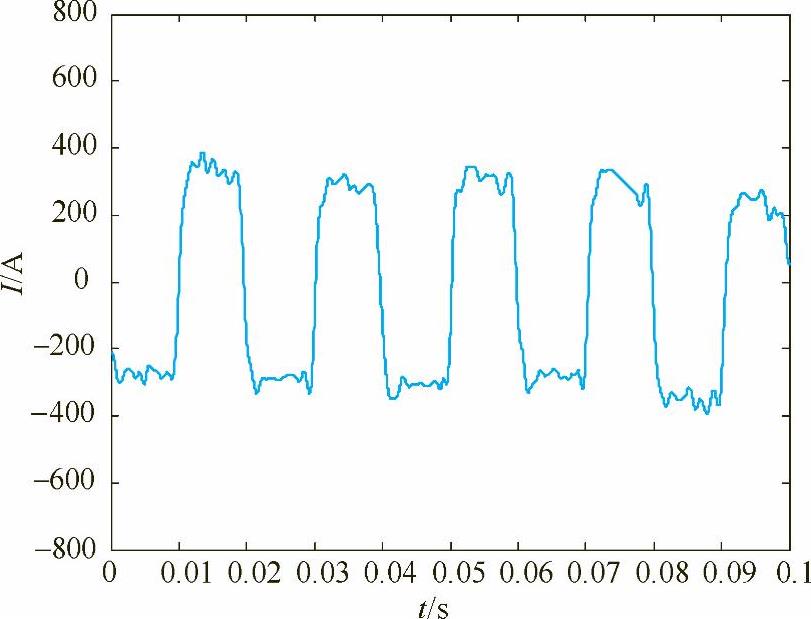
图4-14 交流方波埋弧焊电流信号EMD分解后重构的时域图