常用小波类型及其应用特点

在小波变换过程中，可用的小波函数有多种，常见的小波函数有Haar小波函数、Mexihat小波函数、gaussian小波函数、Morlet小波函数、Meyer小波函数、Daubechies小波函数，也称db小波函数、Coiflets小波函数、双正交bior小波函数等。图4-2所示为Haar小波函数，是数学家Haar于1910年提出的正交函数集，它是小波分析中最早用到的、也是最简单的正交小波函数，它是[0，1]范围内的矩形波。其定义为

图4-2 Haar小波函数

Mexihat小波中文名又称为墨西哥草帽小波，也称Maar小波，如图4-3所示，其定义为

图4-3 墨西哥草帽小波函数

式中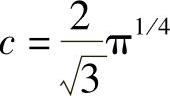，墨西哥草帽小波不是紧支撑的，也不是正交的，但它是对称的，可用于连续小波变换，如常用于计算机视觉中的图像边缘监测。

高斯小波是由一基本高斯函数对时间求导数而得到的，如图4-4、图4-5所示，其定义为

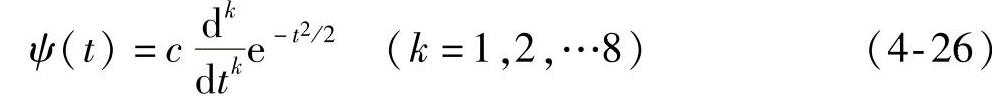
图4-4 叉数为k=4的高斯小波函数

(www.xing528.com)

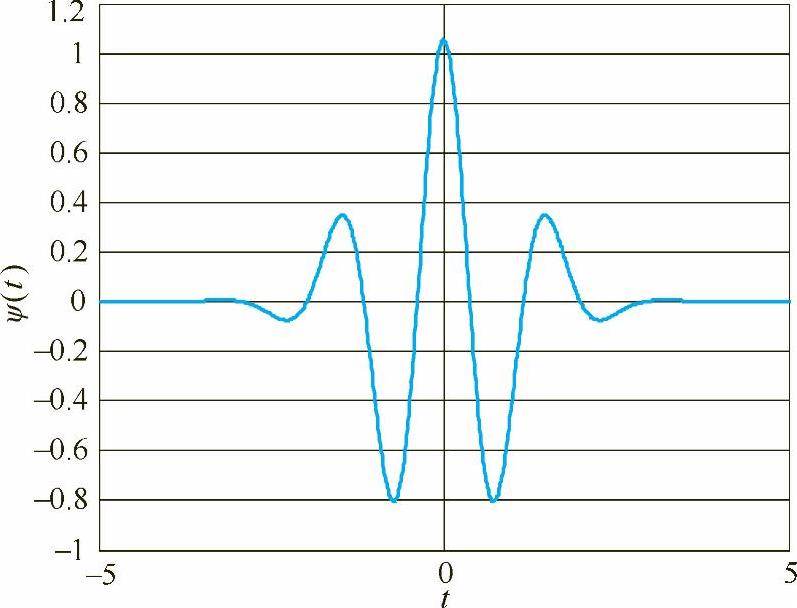
图4-5 叉数为k=8的高斯小波函数

其中c为定标常数，用来保证ψ（t）2=1。该小波不是正交的，当k取偶数时，ψ（t）偶对称；当k取奇数时，ψ（t）为反对称。

Morlet小波是一个具有高斯包络的单频率复正弦函数，如图4-6所示，其定义为

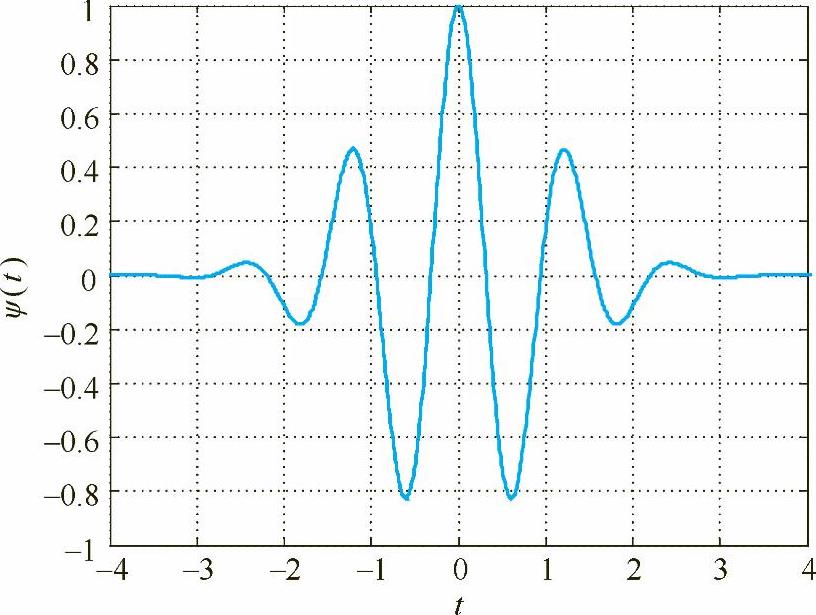
图4-6 Morlet小波函数

由于考虑到待分析的信号为实信号，所以在MATLAB中将式（4-27）修改为

并且取ω₀=5。Morlet小波不是正交的，也不是双正交的，该小波是对称的，常用于连续信号变换，是一种应用较为广泛的小波。

Meyer小波是Meyer于1986年提出的，如图4-7所示，该小波无时域表达式，它是由一对共轭正交镜像滤波器组的频谱来定义的，它是正交的、双正交的。除上述常用小波外，另外还有Daubechies小波，也称db小波，Coiflets小波、双正交bior小波等，它们都是常用的小波。

图4-7 Meyer小波函数