多轴协调运动控制技术优化方案

协调运动控制也称连续轨迹控制。在数控车、铣床，雕刻机、激光切割机、激光焊接机、激光雕刻机、快速成型机、超声焊接机、火焰切割机、等离子切割机、水射流切割机等等都有它的应用。

1.直线圆弧插补法

（1）直线插补法

1）直线插补算法。直线插补的算法很多。这里介绍的是，基准轴输出为主，辅助轴输出配合累加插补算法。此算法使用时，起始点为当前位置，终点可按直角坐标的X、Y值，以脉冲为单位选定。同时，还要选定所在象限。用选定象限确定脉冲输出的方向。如第一象限，则X为正向，Y也为正向。如二象限，则X为反向，Y为正向。其它象限类推。在执行程序时按步计算，按步输出脉冲，而方向用方向信号控制。

所谓基准轴，就是终点坐标值较大的轴。每一步它都输出脉冲，只是当辅助轴有脉冲输出时，它先让辅助轴输出，而在后一个周期。它才输出。辅助轴是否输出，用累加的方法确定。

累加的过程是，用自身的终点坐标累加，当大于基准轴的终点坐标时，输出一个脉冲，并把累加值被基准轴的终点值减，其“差”又作为累加值存储。该算法的框图如图5-51所示。

图5-52所示为一个插补运算实例。

从图知，该例的X轴终点坐标为9，而Y轴为3。可知，应选X轴为基准轴，而Y为辅助轴。从框图知，一开始就累加辅助轴的终点坐标值。但它仅3，比基准的终点坐标值9小，故仅基准轴输出脉冲，走第1步。接着，继续累加辅助轴的终点坐标值。这时累加值为6，比基准的终点坐标值9小，故仅基准轴输出脉冲，走第2步。接着，再累加辅助轴的终点坐标值。这时为9，不比基准的终点坐标值9小，故仅辅助轴输出脉冲走第3步。进而累计值被基准轴的终点值减，其“差”为0，并以0作为新的累加值。之后如图5-52所示，4、5、6又是X轴输出；7是Y轴输出；8、9、10又是X轴输出；11是Y轴输出；12又是X轴输出。

可知，本算法的进给的速度是恒定的，每次都只有一个脉冲。这有利于在切削加工中应用。

2）直线插补程序实现。程序是按算法编的，也是算法的具体化。其基本程序如图5-53、图5-54、图5-55所示。图5-53所示为步进工作起动及初始化程序。图5-54所示为X是基准轴时的脉冲输出控制程序。至于Y是基准轴时的脉冲输出控制程序与此类似，故不重复。图5-55所示为终点及方向控制程序。这里方向控制仅针对两个象限，其它两个象限略。

PLC的步进起动程序用了基本的起、保、停逻辑。“步进起动”ON，则“步进工作”ON，并自保持。直到“步进完成”ON其常闭触点把“步进工作”OFF。这里并联“再起动”，为了选定新的程序后重起动的需要。

这初始化程序则多是微分执行的。其功能是判断那个轴为基准轴、传送坐标值及使参数回到初始值。显然，不进行初始化，程序是无法正确执行的。

图5-51 半累加直线插补算法框图

图5-52 插补实例

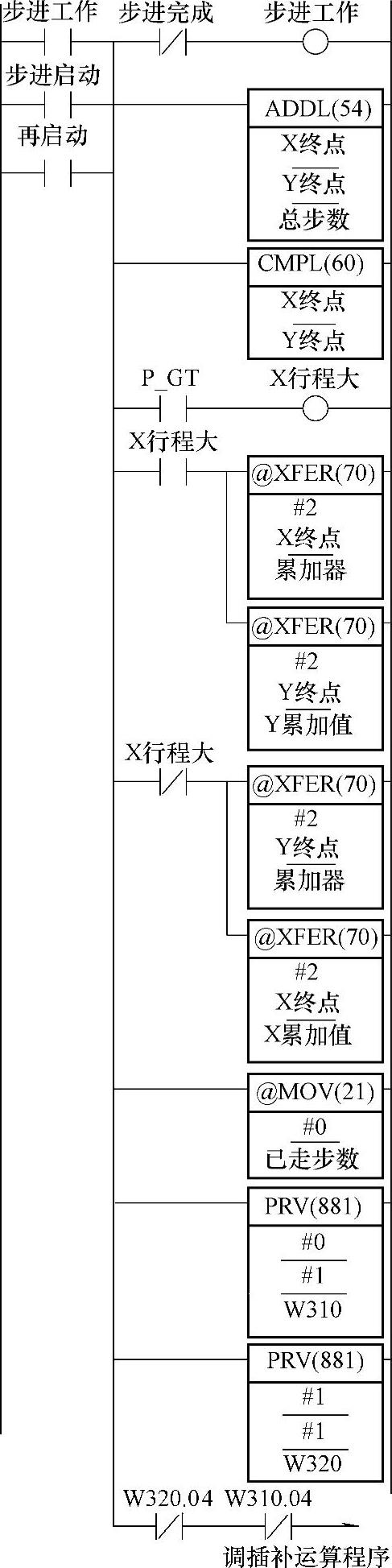
图5-53 步进工作起动及初始化程序

另外，还要调用PRV指令。读取脉冲输出状态。如图5-53所示，如果W320.04及W310.04均OFF，说明两个口均已完成脉冲输出，即可调新的插补运算。至于工作节奏，可控制脉冲输出频率实现。

图5-54所示为当X是基准轴时，脉冲输出控制的梯形图程序。

如图5-54中“X行程大”ON，意味着X为基准轴。正如算法框图指出的，它先把“y累加值”加“y终点”，其“和”赋值给“y累加值”。然后，把“y累加值”被“累加器”减，其“差”赋值给“Y_TEMP”。参看图5-53知，此“累加器”即为X轴的终点坐标值。如不够减，即它小于“累加器”，则“y加进位”OFF，X轴输出脉冲。如足够减，即它大、等于“累加器”，则“y加进位”置位。进而，把“Y_TEMP”，即这个“差”赋值给“y累加值”，“y步进”置位，输出脉冲。同时，把“y已走”置位。“y已走”置位的目的是，在这个工作周期，不让X轴输出脉冲。但临退出本程序段时，用“y加进位”ON，把“y已走”复位。为下一周期执行X轴发送脉冲作准备。

当下一次，再进入本程序段时，由于“y加进位”仍为ON，故Y轴的累加不进行。而使“X步进”置位，进行X方向步进，同时使“y加进位”复位，为新一次的Y轴累加及相应操作作准备。

以上程序讲的都是“X行程大”ON的情况，而“X行程大”OFF，与此类似。在本程序最后，使“已走步数”加1，为控制步进是否完成提供依据。

每执行一次本段程序，都会产生脉冲输出，不是使在X方向，就是在Y方向走一步。所以，执行完本程序，都将使“已走步数”加1。

提示：在这程序中，如不用“y已走”信号进行控制，基准轴总是输出脉冲，而辅助轴累加值超过基准轴终点值时，也输出脉冲。运动轨迹将有时是走坐标轴的平行线，有时走斜线。速度将是不均匀的。

图5-55所示为终点及方向控制梯形图程序。

图5-54 X是基准轴时脉冲输出控制

图5-55 终点及方向控制程序

它主要是判断到了坐标终点了没有？如到，则置位“步进完成”。再看图5-53可知，此信号将使“步进工作”停止。

此外，此程序还依选定的象限，对X、Y轴运动方向做了确定。图中只列出1、2象限的程序，3、4象限也类似。

（2）圆弧插补法

在两个坐标点间，如果要是曲线怎么办？把这曲线分成若干直线，用上述分几个直线段进行插补。这样，上述程序使用时及编程时，就要做分析：要分几段才能满足精度要求？每段的终点坐标是多少？然后，进行参数设定，并送入PLC。再运行上述程序，也可实行两点间的曲线运动。早期数控实现曲线运动，加工曲面就是这个办法。结果是，使用的数据很多，编程（划分线段那样的编程）工作量很大。给数控的应用带来很大的不便。

在两个坐标点间，要走曲线第二个办法是用圆弧插补，有的还用其它二次曲线插补。这样插补比直线插补最大的优点是，达到相同的精度，所需的线段少，编程简单。但插补的运算复杂些。而后者是系统设计的问题，最终用户可不必考虑。

1）逐点比较算法。同样圆弧插补，方法也较多。这里介绍的是较常用的逐点比较法。逐点比较法的基本思想是，走一步，比较一次。也可反过来说，比较一次，走一步。比较什么？看当前的位置是在圆弧内，还是圆弧外？如在圆内，则往外走。如在圆外，则往内走。为此，插补要分象限、按运动方向进行。如在第一象限，逆时针运动：只能是正Y及负X运动，而发送正Y向脉冲将是往外走；发送负X向脉冲将是往内走。如图5-56所示。其它各象限也都有相应的规律。

图5-56 一象限逆时针运动

比较的关键还在于，怎么知道是在圆上、在圆内，还是在圆外？不难。如圆的半径为R。如在圆上，则X的平方与Y的平方之“和”减去R的平方，即Δ，为0。如在圆内，则Δ小于0。如在圆外，则Δ大于0。

只是这里都是平方计算。但如只计算相对值，即向某方向走了一步后Δ变化就不用平方计算了。如现在圆上，显然以下等式成立：

X²+Y²-R²=0

这时，如在正X向走一步，即X变为X+1，是否在圆内？可按下式计算：

Δ=（X+1）²+Y²-R²=X²+2X+1+Y²-（X²+Y²）=2X+1

即只计算2X+1，如为正，则在圆外。同理，如正Y走一步则计算2Y+1；如负X走一步则计算-2X+1；如负Y走一步则计算-2Y+1。而这些计算没有平方，只是乘2及加1，较简单。正是这样，逐点比较法用的很多。

图5-57 第一象限逆时针插补的算法

图5-57示的为第一象限逆时针插补时的算法框图。

从图知，先是初始化，再判断是否Δ>0？若Δ>0，则向负X走一步；若Δ≤0，则向正Y走一步。再计算Δ及X或Y值。判断是否到终点，若到终点，则退出。若不到终点，则返回判断，重复上述过程。图5-58所示为用此算法计算的简单运动实例。

从图知，它用第一象限逆时针插补的算法。X起点为5，终点为1。Y起点为1，终点为5。其计算与走步情况如下：

第1次时，Δ=0，走Y，计算Δ为3；

第2次时，Δ=3，走X，计算Δ为-6；

第3次时，Δ=-6，走Y，计算Δ为-1；

第4次时，Δ=-1，走Y，计算Δ为6；

第5次时，Δ=6，走X，计算Δ为-1；

第6次时，Δ=-1，走Y，计算Δ为8；

第7次时，Δ=8，走X，计算Δ为3；

第8次时，Δ=3，走X，计算Δ为0，到终点，停。

提示：这里X起点、Y起点是以圆心为原点计算的。X终点、Y终点也应是如此。即这4个数是有相关关系的。

2）逐点比较法程序实现。圆弧插补初始化程序如图5-59所示。

从图5-59可知，该程序先是“起、保、停”逻辑。“步进起动”ON，将使“步进工作”ON，并自保持。到“步进完成”ON，则“步进工作”OFF。这里并联“再起动”，为了选定新的程序后重起动的需要。

进入“步进工作”后，按算法进行初始化。计算总步数，把X起点赋值给X，Y起点赋值给Y，清零“已走步数”、并把0赋值给“Δ”。对图5-59用“某大常数”赋值给，以作为Δ的基数。目的是使Δ怎么加减，也不至于出现负值（因为CPM2A用的是双字BCD码运算，出现负数不好处理）。计算后的Δ则与“某大常数”比较，而不与0比较。效果是相同的。这也算是编程因地而为的一种技巧。

图5-60所示为第一象限、逆时针运动插补时圆弧插补的运算程序。

从图知，它先是比较，把Δ与“某大常数”比较：小于或等于时，发送正Y脉冲，并作算法要求的相应计算；大于时，发送负X脉冲，并作算法要求的相应计算。

程序后面为“已走步数”加常数1，并与“总步数”比较，如相等或大于时，则“步进完成”ON。这将使“步进工作”OFF。

图5-60所示程序不仅可用于第一象限、逆时针运动的插补控制，还可用于第三象限、顺时针运动。其它如图5-61所示，如第一象限、顺时针运动及第三象限、逆时针运动一样，在圆内，则走+X，在圆外，则走-Y；如第二象限、顺时针运动及第四象限、逆时针运动一样，在圆内，则走+Y，在圆外，则走+X；如第二象限、逆时针运动及第四象限、顺时针运动一样，在圆内，则走-X，在圆外，则走-Y。具体梯形图程序可在图5-60的基础上稍加修改即可。

图5-58 计算实例

图5-59 圆弧插补初始化程序(www.xing528.com)

图5-60 第一象限、逆时针运动插补时圆弧插补运算程序

（3）插补程序合成

以上介绍的程序只能做一小段运动轨迹的插补。实际曲线复杂时，要做多段插补。多段中，可能有各个象限的小直线，还可能有各个象限、逆时针或顺时针的小圆弧。怎么把这样一段段运动连贯起来，就是插补程序合成要解决的问题。

图5-62所示是一种用程序控制实现的算法。

图5-61 各象限顺、逆时针运动

从图知，“程控起动”后，先传送“程控初始化数据”。这些数据有程序总数（有多少上述小段程序？）、“当前程序号”置1、数据指针初始化（控制数据存放首地址）等。然后起动“步进工作”。“步进工作”开始时，先执行初始化程序（如图5-47、图5-53所示），随后调“步工作子程序”（如图5-47、图5-48或图5-54所示）。每执行一次，都要判断步是否完成，如未完成，则相隔一个“脉冲时间间隔”，再调此子程序；如完成，则使“步进工作”OFF，并修改步参数指针、“当前程序号”加1，并比较“当前程序号”是否大于“程序总数”。如不大于，则进入再起动，再使“步进工作”开始；如大于，则已完成所有程序段的控制，将结束程控。

图5-63所示为实现此算法的梯形图程序。

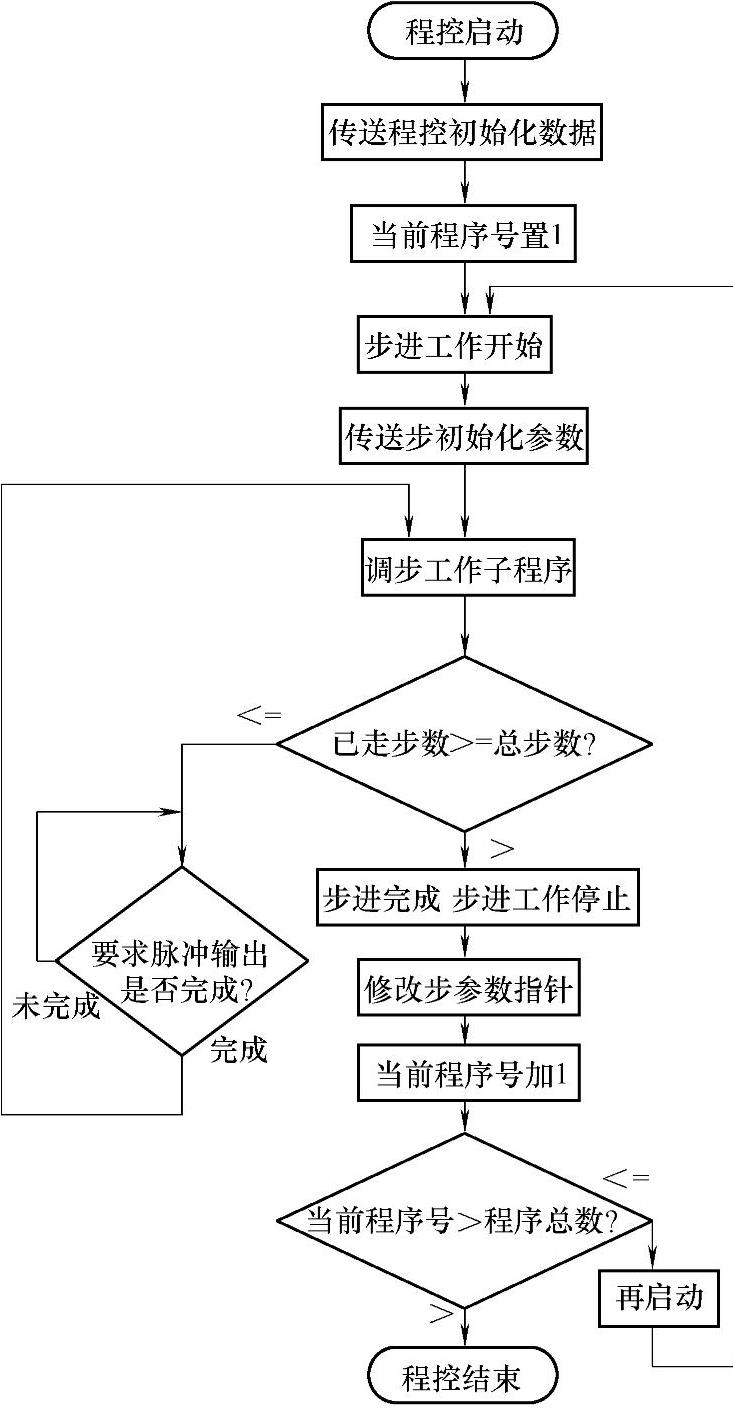
图5-62 程序控制算法

图5-63 PLC程序控制梯形图程序

从图知，当“程序工作”OFF时，“程序完成”复位。当“程序起动”ON，则“程序工作”ON，并自保持。之后进行初始化：“当前程序号”置1，把800传“指针”（用作DM间接地址初值，即有关插补运算数据预先存储在DM800开始的地址中）、“程序段数”传给“程序总数”。同时，执行块传送指令，把DM800开始的9个字数据，传送给“图形象限”等字或双字。这些数据有：“图形象限”、“X终点”、“Y终点”、“X始点”、“Y始点”。第1项占一个字，后4项每项占两字。这9个字是按插补要求，预先存于从800开始的DM数据区中的。有了这组数据，只要“步进工作”ON，即可定时调相应子程序，先进行步初始化（如图5-47、图5-53所示），后定时调相关程序（如图5-48、图5-49、图5-54所示），即可进行相应控制。

当完成要求运动的总步数时，则“步进完成”置位。进而使“步进工作”OFF。同时，修改指针，使“当前程序号”加1，并“指针”加9，指向新的一组数据。而且，当“步进工作”OFF后，从梯形图最后一个梯级知，它将使“再起动”ON，并自保持。这“再起动”ON将重新使“步进工作”ON，并自保持。同时使“步进完成”复位。“步进工作”再次ON，先也是步初始化，可得到新的一组“图形象限”等控制数据。进而，又可根据脉冲输出完成情况调用相应子程序，作下一个步的控制。至于程序节奏将由设定的脉冲输出频率确定。

当一段插补程序运行结束，都做“当前程序号”是否大于“程序总数”判断。如果为“大于”，则“程控完成”ON，它将使“程控工作”、“步进工作”OFF，使整个程序控制结束。

2.目标追踪控制

上述插补算法是早期数控控制机常用的算法。随着计算机工作速度的提高及计算能力的增强，如果对象的运动轨迹有确定表达式，也可直接目标追踪实现轨迹控制，而不必作分段插补。

（1）目标追踪算法

1）根据对象运动轨迹表达式，选定一个合适的参变量，把表达式转换为参变量方程。要确保参变量的单值变化能覆盖整个运动轨迹；

2）使参变量微小增（或减）变化（变化范围应覆盖整个运动轨迹），逐一计算目标值X、Y的变化；

3）判断目标值X或Y是否出现单位值增、减的情况，如出现，输出脉冲，使控制对象在X或Y坐标方向作增或减1运动；

4）判断是否到达终点，否，则继续使参变量微小增减，重复上述2）、3）过程；是，则控制结束。

图5-64 螺旋曲线图型

（2）目标追踪算法实例

以下以图5-64所示的螺旋线轨迹为例，介绍此算法设计及其程序实现。螺旋线用参变量θ，表示它的轨迹。

如图所示，其中ρ与θ及X、Y与θ、ρ间的关系式如下：

ρ=k·θ

X=ρ·cosθ

Y=ρ·sinθ

θ从0到4π，将覆盖整个轨迹。该图表示了在X、Y坐标上“步进”，完成这个运动轨迹的控制情景。图5-65所示为这个算法图解。

从图知：

1）初始化：使目标坐标值X、Y、实际坐标值X0、Y0及参变数θ均置0，同时，把“某较小数”赋值给Δθ及设定螺旋圈数n及系数k。

2）计算：按图示公式，计算目标值X、Y。这里“某较小数”要小到加此值后，最多只能使X或Y的增量为1。

3）比较：做4个比较，如都为“否”，则使θ加Δθ。否则如X与X0比较有一个“是”，则修改实际坐标值，作相应步进。等待脉冲时间间隔后再对Y与Y0进行比较。后者比较若“是”，则也修改实际坐标值，作相应步进。等待脉冲时间间隔后进入下一步。

4）判断：判断是否达到终点，即Y0=0及X0=2π∗n∗k是否成立。是退出控制，不是又使θ加Δθ，回到（2）。

可知，按图示算法，将用一段段平行于X、Y坐标的小短线，近似地走出螺旋线来。这个近似最大误差将不大于一个步进的行程，即脉冲当量。

（3）目标追踪算法梯形图程序实现

图5-66所示为实现上述算法的PLC梯形图程序。当未达到终点时，每隔一个脉冲间隔时间或每当完成要求的脉冲输出，将调用一次本程序。但在此没有列出工作控制及终点判断等有关程序。

图5-65 螺旋线轨迹直接目标追踪控制算法

从图知，进入本程序时，先比较Xi与X0、Yi与Y0是否相等。有任一组不相等时，则JMP1与JME之间的指令将跳过，直接进入进一步比较，确定是否设置“步进”。如满足一个设置“步进”条件，则输出脉冲，并随后传送数据，使不等的变成相等。这样，下一次再进入时，此不相等的条件将不存在了。

其后是在FOR、NEXT间的指令，最多可重复执行100次。其任务是使θ增Δθ，按螺旋线的参数方程，进行ρ、Xf及Yf点计算。然后对Xf、Yf取整，并相应存于Xi、Yi中。接着进入比较Xi与X0、Yi与Y0是否相等。由于Δθ是“某较小数”。要求这个数要小到，带给θ变化而引起的Xf、Yf的增减数不能大于1，所以，这里如不相等，也仅相差1，可确保每次步进仅一个脉冲当量。Xi与X0、Yi与Y0比较结果有4种情况：

1）Xi与X0及Yi与Y0均相等，则继续重复执行，又使θ再增Δθ，及进行ρ、Xf及Yf浮点计算。然后对Xf、Yf取整，并相应存于Xi、Yi中。进而又回到这里比较。显然，由于螺旋线的X、Y坐标总是要随θ的增加而变化的，一般在100次内总能出现不等的情况。

2）Xi与X0相等，所以，不会出现步进。而Yi与Y0不等，将使Y步进。并把Yi传送给Y0。同时执行BREAK指令，跳出重复执行，跳出本程序。

3）Xi与X0不等，而Yi与Y0相等，将使X步进。并把Xi传送给X0，跳出重复执行，跳出本程序。

4）Xi与X0、Yi与Y0均不等，将先使X步进。并把Xi传送给X0，跳出重复执行，跳出本程序。但下一次执行本程序时，由于Yi与Y0不等，将直接进入这个比较使Y步进。这样处理的目的是，可做到，每次“步进”只能在一个坐标上进行，可得到均匀的运动速度。

图5-66 螺旋线运动轨迹控制梯形图程序

以上讨论的螺旋线是逆时针，从第一象限开始的。还可为顺时针，或其它象限开始的。这些控制都可在本程序的基础上，稍作修改也都可实现。

（4）目标追踪算法ST语言功能块实现

ST语言擅长于执行运算程序，所以用其设计本算法的程序实现是较为简单的。以下为它的功能块程序。

使用的变量声明有输入、输出及内部变量。

输入变量有：

输出变量有：

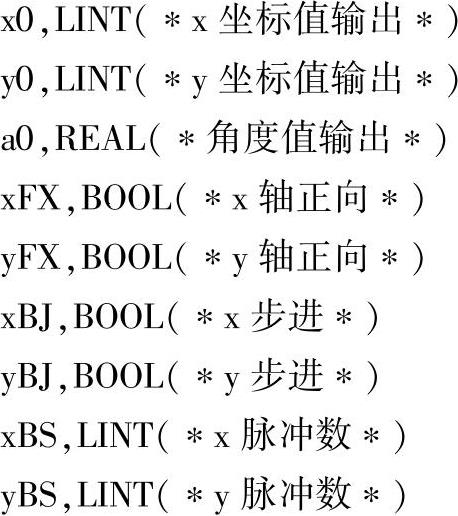
中间变量有：

功能块使用语句如下。其含义见语句后的注解。

图5-67所示为功能块调用梯形图程序。

从图5-67知。它有4个梯形条。每梯形条的功能见注解。具体说明略。

提示：直接目标追踪控制的算法，不仅可用于本例的螺旋线轨迹控制，对于其它曲线甚至多维曲线轨迹控制，只要它的轨迹可用参数方程单值表达，也都可由本算法实现。只是要求PLC有很高的运算速度。

图5-67 功能块调用梯形图程序