开环控制及其实现方法

1.定值控制

不用控制结果信息，使调节量（被控量）保持所要求定值的控制，称开环定值控制。要实现这个控制，首先要弄清控制量及干扰量与调节（被控）量间的量化关系。

这个关系已在上一节作了讨论。弄清这个关系，就可方便地进行开环定值控制了。具体的办法是，根据要求得到的调节量，依它与控制量间的对应关系，决定要输出的控制量。

这么处理的不足是，无法考虑干扰量的影响。事实上，在多数情况下，存在种种干扰是不可避免的。这样，就很难得到较好的定值控制的效果。这也是开环控制用的较少的重要原因。

2.程序控制

这里讲的程序控制是指，使被调节量按预定规律变化所作的控制。这预定规律可根据要求任意设计。如图4-25所示，若运动部件起动后，先作等加速度运动；增速到Max值时，速度保持这Max值，作等速运动；到总行程“行程快到”后，作等减速度运动；减速到Min值后，速度保持Min值，作等速运动，直到行程到“行程到”时，运动停止。这就是一种程序控制规律。设计符合这样规律的控制就是这里指的程序控制。

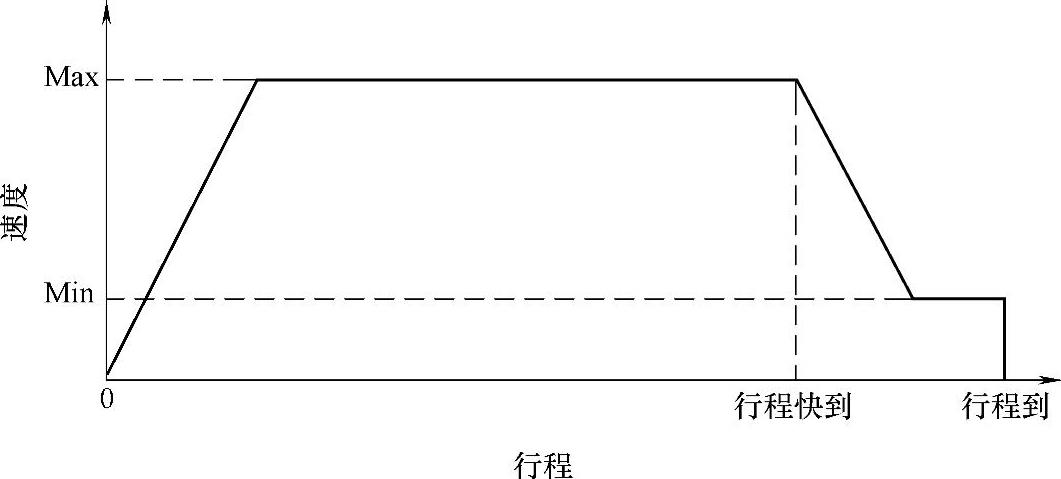
图4-25 运动速度与行程关系

图4-26所示为实现这个控制的程序。当然，在使用时，还须把这里的模拟量“输出”作功率放大，以加载给直流电动机，或用“输出”控制变频器输出频率，用变频器加载给交流电动机。而且，这电动机还要去带动相应的运动部件。

图中“输出”是加载给电动机的模拟控制信号。可理解为0～5V或10V电压。此电压高，直流电压也高，或变频器的输出频率也高；用它驱动电动机时，电动机的转速也高；进而部件运动速度也快。所以，控制此数值即可控制部件运动速度。

为了便于说明，图中用的都是符号地址。如图所示，“起动”信号ON后，“运行”将ON，并自保持。这时，由于“减小”OFF，其常闭触点ON，故“增加”ON。

“增加”ON，且D0小于Max时，将使D0每隔100ms加1一次，十六进制数运算操作上，使数据存储器D0每经100ms，加1一次。而此D0的值总是传送给“输出”，因为它的传送条件总是P_ON，均为常ON特殊继电器。这样，由于D0值的增大，“输出”也将随之增大，因而，所控制部件的速度将增速。

当D0增到Max值时，将保持Max值，不再增大。这时，部件将作等速运动。

当部件运动时，将产生“脉冲输入”信号。每输入一个脉冲，将使D1加1。

当D1增加到等于或大于“行程快到”值时，“减小”ON，其常闭触点将使“增加”OFF。同时，使数据存储器D0每经100ms，减1一次。这样，由于D0的减小，“输出”也将随之减小，因而，所控制部件的速度将减速。

当D0减小到Min值时，将保持Min值，不再减小。这时，部件将作等速运动。

当运动到“行程到”值时，“停止”ON，其常闭触点将使“运行”OFF。D0、D1回到0，整个控制完成。

应指出的是，这里的开环控制指的是速度控制。而行程控制还是闭环的。部件运动行程用脉冲输入反馈。如果运动速度较快，脉冲频率较高，还可用高速计数器处理此过程，这将在本书第5章还会有所讨论。

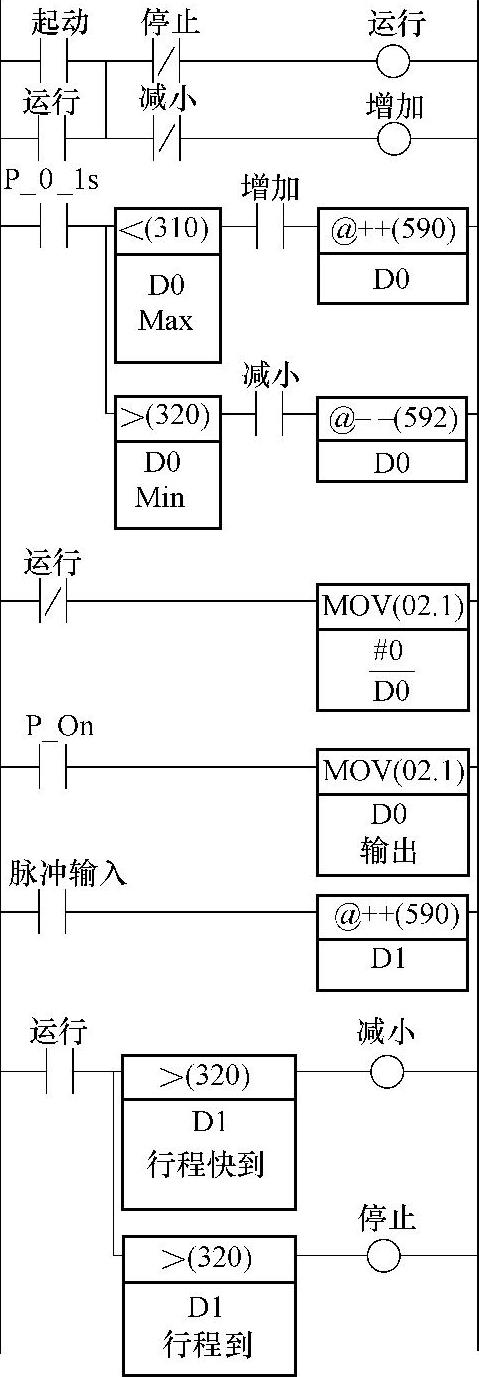
图4-26 运动速度控制程序

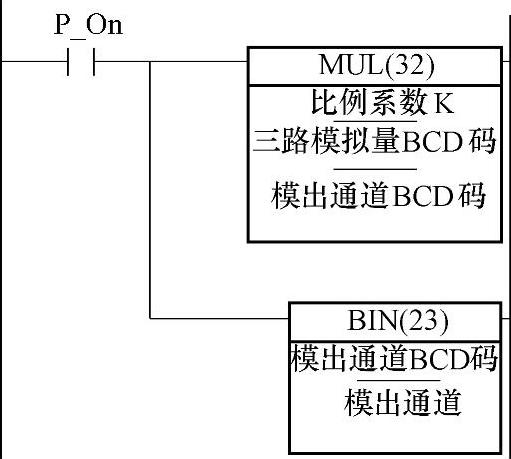
图4-27 比例控制梯形图程序

3.比例控制

比例控制的实例如图4-27所示。它可使流量Q_b按比例k，跟随流量Q_a变化。图4-27为它的相应程序。

从图知，这里的“模出通道”的BCD码值为“三路模拟量BCD码”与“比例系数K”的乘积。再经转换为十六进制码，然后输出给“模出通道”，即可使“模出通道”控制的模拟量，按比例系数K，随“三路模拟量BCD码”的变化而变化。

还可能实现多值比例控制，图4-28为与其对应的梯形图程序。这里有两个比例器K1、K2，都由输入量Qa控制，以保证实现Qb1=K1×Qa、Qb2=K2×Qa的比例关系。

从图知，这里的“模出通道1BCD码”、“模出通道2BCD码”值为“三路模拟量BCD码”与“比例系数K1”、“比例系数K2”的乘积。再经转换为十六进制码后输出给“模出通道1”、“模出通道2”，即可使“模出通道1”、“模出通道2”控制的模拟量，按比例系数K1、K2，随“三路模拟量BCD码”的变化而变化。

提示1：这里的乘后的“积”为双字，要确保它的“积”处在模出通道的有效值范围之内。

提示2：如K1、K2不是整数，可先把K1、K2乘10、或乘100等，使其变成整数，然后再作这里的乘。得出结果后，再用双字长除指令，把“得出结果”的除10、或100等，使最后的结果处在模出通道的有效值范围之内。

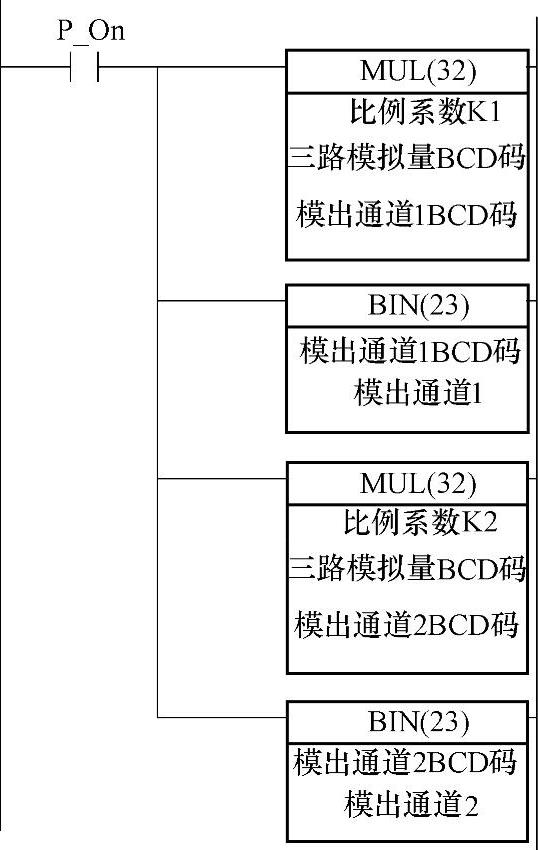
图4-28 多值比例控制梯形图程序

4.补偿控制(www.xing528.com)

图4-29所示的为前馈控制，也就是这里讲的扰动补偿控制。

如该图所示，加热物料流入量就是它的主要干扰因数。如用一传感器检测热物料流入量，并通过模入单元把检测到的这个量送入PLC，再由PLC按干扰规律对其进行处理（按扰动影响规律，把输入变换成相应的输出），然后再通过模出单元去控制蒸汽阀，即可实现调节蒸汽的前馈控制。从而使加热物料流入量对容器温度的干扰，得到相应补偿。

可看出，这里模入、模出、PLC及其处理程序，即为该图的前馈补偿器。而在这几项中，最难的是弄清扰动影响规律。

一般讲，确定扰动影响规律有两个方法：解析法，探求相应函数关系；实验法，检测一系列相关数据，建对应数表。

对简单的过程，如负载电流对直流发电机的输出电压的影响，用解析法就比较好求。因为

U_d=E-I_d×R₀

U=U_d-ΔIR₀=E-（I_d+ΔI）R₀

式中 U_d———额定输出电压；

E———发电机电动势；

I_d———额定负载电流；

ΔI———实际电流与额度电流差值；

R₀———电动机电枢电阻。

可知，负载电流对输出电压的扰动是线性的。要补偿它的扰动，可提高电动势E。而

E=CΦn

式中 C———电动机常数，与电动机的结构等因素有关；

Φ———激磁磁通；

n———电动机转速。

在这3个量中，较便于处理的是增加辅助激磁线圈，以增加的激磁磁通ΔΦ。如用这个辅助激磁磁通ΔΦ，所多得到的电动势ΔE正好等于ΔIR₀，则可使电流变化对电压的干扰得到补偿。即：

ΔΦ=（R₀）÷（C×n）×ΔI

有了这个关系，把用模入单元检测到的ΔI值，按（R₀）÷（C×n）×ΔI关系，变换为ΔΦ，并送模出单元，去产生辅助激磁磁通。即可实现这个补偿。

这里的按（R₀）÷（C×n）×ΔI关系变换，对PLC来说，运用一些运算指令即可实现，并不难。

如图4-6所示的例子。弄清加热的物料流入量（扰动量）、蒸汽流量（控制量）与容器温度（调节量）的关系，从中找出解析关系，也可设计出相应的前馈补偿程序。

但是，如果找不出这些量之间解析关系，那只好用实验法。它的要点是，通过实验，逐个测出不同的扰动量时，要用多大的控制量，才能使系统的调节量达到期望值。然后，列出一个数表，存于PLCDM区中。

这种情况下的扰动补偿程序，就是使用好这个数表。图4-29即为这种程序。

从图知，这里只用两条主要指令。一是“MOV”指令，用“一路模拟量BCD码”对指针赋值。另一为“BIN”指令，把指针指向的DM地址的内容，转换为十六进制码，并传送给模出通道。与图4-6对照，这里的“一路模拟量BCD码”与“进料变送器”对应，“模出通道”与“调节阀”对应。

这里的程序较简单，但执行这程序前必须对指针DM0指向的DM区先赋值。有时，也可能从“一路模拟量BCD码”到指针赋值，或从指针指向的内容到“模出通道”之间，还要作一些插值运算，以使控制输出更精确些。

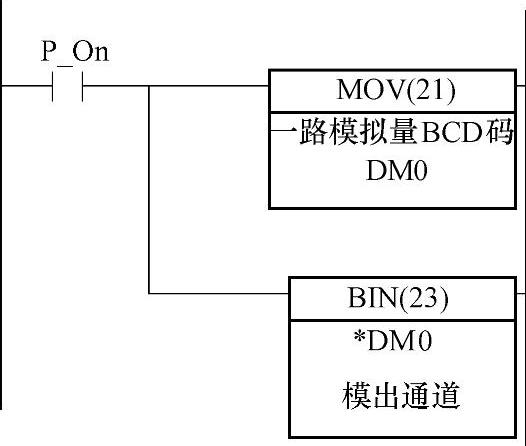
图4-29 补偿控制梯形图程序

从上讨论可知，要设计前馈控制程序，首先要找出主要的干扰因数，并弄清扰动量、控制量与调节量的关系。否则，无法设计这种控制程序。这也是这种控制使用的局限性。

提示：比例控制及补偿控制，实际也就是随动控制，都是使一个或一组模拟量随另一模拟量的变化而变化。只是这里仍是开环的，其控制结果没有反馈给控制程序。

应指出的是，这里讲的控制输出，都是用模拟量输出单元。其实，用脉宽可调的脉冲或比例可调ON/OFF继电输出也是可以的。