PLC系统开环特性及其测量方法

开环特性有静态特性及动态特性两种。静态特性是指，系统状态稳定后调节量（被控量）与控制量间的对应关系。而动态特性是指，系统状态在开始变化到稳定的过程中，调节量（被控量）与控制量间的对应关系。

1.静态特性

（1）控制量及干扰量与调节（被控）量间的量化关系。在本章开始时曾提到，调节量、控制量及干扰量。用定量分析看，它们之间关系为

r=f（c，t₁，t₂…）

这里，r为调节量，是表示被控系统的状态、行为、性能或功能的物理量，如温度、压力、转速，等；

c为控制量是，经PLC处理后、产生控制作用的输出量，如模出单元的现值，脉冲量的脉宽（占空比），开关量输出的工作时间与工作周期比等。简单的控制系统一般仅一个控制量；

t₁，t2…是使系统的状态与行为产生所不希望变化的一些物理量，如负载电流、力矩。干扰量一般较多，但主要的可能也不多。

（2）开环放大倍数K。调节量增量与控制量增量之比。如调节量与控制量是线性关系，则K为常数，否则，K将随着控制量变化有所变化。

控制量可以是模出单元的输出值，也可是（如为脉宽调制输出）脉宽值，或别的量。依系统的构成而定。

调节量也可用模拟量输入，或脉冲量输入表示。前者，如模入单元的现值。后者，如脉冲量输入的频率。对应的也可有相应的相对的K值。也要按照系统构成而定。

图4-24所示为某电动机转速控制系统的调节量（脉冲频率，用以反映被控制电动机的转速）与控制量（模出单元输出现值，用以控制电动机转速）间的一个典型的关系。只是像这样完全线性的关系是不多的。

这里有两点要说明：

1）PLC模出单元有输出值，但可能系统仍无输出，即脉冲频率为0，系统输出存在死区。如该图在0～1F之间时，脉冲频率均为0。

2）输入输出关系曲线，即特性线是离散的，纵横坐标都应为整数值。(www.xing528.com)

K值反映控制系统的灵敏度。K值大，说明控制量不大的变化，可能会产生较大的调节量的变化。

此外，系统的扰动量对调节量也会有影响。这可用开环扰动系数T₁、T₂……表示。

开环扰动系数T₁、T₂指，调节量与某扰动量之比。如扰动量与控制量是线性关系，则T₁、T₂为常数，否则，T₁、T₂将随扰动量不同而有所不同。

T值反映干扰量对系统的作用强度。T值大，说明干扰量不大的变化，可能会产生较大的调节量的变化。

但，一般讲，要弄清干扰量与调节量间的关系是不易的。

（3）输出分辨率。PLC输出的变化是不连续的，是按输出分辨率离散变化的。如PLC模出单元为12位时，其分辨率为1/4096。这意味着，模出变化（增或减）的最少值只能是总输出值的1/4096，比此再小是不可能的。

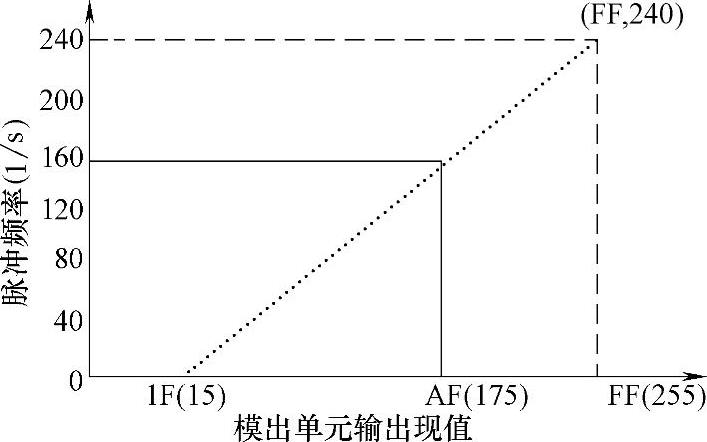
图4-24 电动机的转速与控制量关系

与这个对应的系统输出，即调节量的变化也将是离散变化的。其变化的最小值也将是调节量最大变化量的1/4096。

存在这个离散性说明，要使系统的调节量无误差地处于任一要求的状态是不可能的。但是，这个误差是可控制的。提高模入、模出单元的分辨率即可减少这个误差。

2.动态特性

由于系统是开环的，输入与输出的对应关系又是惟一的，所以，开环动态特性总是稳定的。常规（线性、连续）的系统开环动态特性多是用频率特性衡量，即在其输入端人为地加上单位幅值不同频率的正弦信号，看其正弦输出的幅值变化及其与输入正弦信号的相位差。即所谓幅频特性及相频特性。

而对PLC控制的系统，有“误差”、“断续”及“时延”的特点，不方便用频率特性去反映它的开环特性。最简单是用响应时间，即系统从开始变化到稳定的时间衡量。具体的指标可以是：每单位控制作用，即PLC模出单元的每一分辨率的变化，到系统稳定所需要的时间。显然，从系统对控制作用反应的快速性讲，这个时间是越小越好。