组合逻辑表达式与真值表：详解与应用

1.表达式

继电电路常用到触点，触点代数研究的变量就是这个触点。它是研究触点电路的重要工具，也是研究梯形图逻辑的基础。

（1）有关约定

1）触点变量。继电电路常用到触点，触点变量就是反映触点状态的逻辑量。仅有两个取值，1与0。1代表通，或ON；0代表断，或OFF。

在一个电路中，同名器件有时用它的常开触点、有时用它的常闭触点。常开触点，没有外作用时，是断开的，有外作用时，是接通的。直接用变量名命名，如X，读X。常闭触点，没有外作用时，是接通的，有外作用时，是断开的。用变量名加一小横线命名，如X，读“X的非”。可知，常开与常闭触点，其取值是相反的。

PLC的梯形图没有实际触点，用的是操作数“位”。直接用（读）它，相当于使用常开触点。用（读）它的“非”，相当于使用常闭触点。

2）触点代数运算。触点代数是用指定运算反映触点间的连接。触点并联的运算是“或”，也叫加（+）、或析取。对应梯形图指令就是“OR”。触点串联的运算是“与”，也叫乘（∗，有时乘号省略），或合取。对应梯形图指令就是“AND”。触点串联后的并联，则是乘后和。并联后的串联，则是和后乘。为了明确运算顺序，可使用成对的括号，括号内的运算优先。

此外，还有“非”的运算，也叫求反。上述同名变量的常开、常闭触点间就是“非”的关系。对常开触点求反，即变为常闭触点；对常闭触点求反即变为常开触点；求两次反，又变为自身了。

对应梯形图，如果指令后加“NOT”，则用变量的非。如“ANDNOTX”，是对变量X求反后再“与”。再如“ORNOTX”，是对变量X求反后再“或”。

触点代数未对线圈作约定，不讨论输出对输入的反馈。

（2）表达式与电路对应关系。有了上述约定，实际电路与触点代数表达式之间就有了一一对应关系。以本书第1章第1节的图1-1、图1-2电路为例，除了其中的桥式电路，其它的都可用上述约定的逻辑式子表达。

L=X1∗X2（与图1-1a对应）

L=X1+X2（与图1-1b对应）

L=（X1∗X2）+（X3∗X4）（与图1-1c对应）

L=（X1+X2）∗（X3+X4）（与图1-1f对应）

L=（（X1∗Y1）+（X1∗Y1））∗（（X2∗Y2）+（X2∗Y2））（与图1-2b对应）

这里，等式右边为逻辑表达式，反映了触点间的不同连接。左边为输出变量，也是用电器L。它的取值由表达式及变量的取值决定，反映电路的效果。

图3-2梯形图程序为组合逻辑。也可根据上述约定用逻辑式子表达。具体为

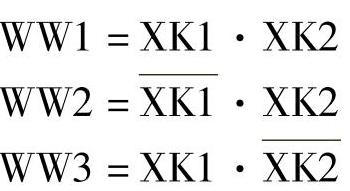
（3）触点运算规则、规律及原则。数与数运算规则有：

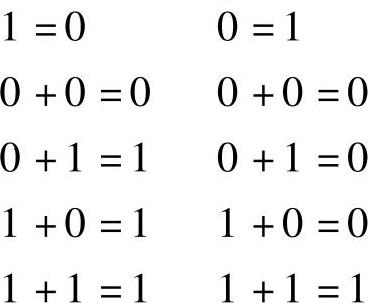
上述诸式是对常数的运算的规则。不难证明，这些规则是符合上述约定的。

把上述约定与命题代数对比发现，触点代数与命题代数是等价的。“这个触点接通”、“这个触点断开”就是命题，“这个触点接通或那个触点接通”就是命题运算，等等。所以，可以把命题代数运算的一些规律移植过来。这些规律有：

交换律 X·Y=Y·X

X+Y=Y+X

结合律 （X·Y）Z=X（Y·Z）

（X+Y）+Z=X+（Y+Z）

吸收律 0+X=X1·X=X

1+X=10·X=0

重复律 X·X·X…X=X

X+X+X+…+X=X

分配律 X（Y+Z）=XY+XZ

X+YZ=（X+Y）（X+Z）逆项吸收律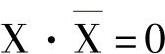

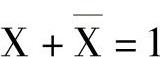
双重否定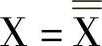律反演律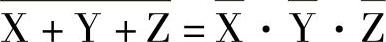

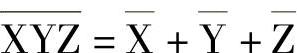
这些规律也完全可用实际电路予以验证。

此外，还有3条原则：

1）反演原则。它是反演律的推广。任何逻辑式子F，若“非”仅出现在变量上，把这个公式中的乘与加对换、变量与变量的非对换、1与0对换，所得的式子G，满足

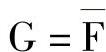
利用它，很易求出与某一电路功能相反的电路。

2）对偶原则。任一逻辑式子F，若非仅出现在变量上，把这个公式的乘与加对换、0与1对换，所得的式子F′称其为F的对偶公式。对偶是相互的，F也是F′的对偶公式。

若有F=G则它的任一对偶F′、G′有

F′=G′

有了这个原则，等式的证明可减少一半。

3）代入原则。任何含有变量A的逻辑式子，如果把所有出现A的地方都代之以一个逻辑式子F，则等式仍然成立。这是因为一个逻辑式子的取值，也和逻辑变量一样，不是1就是0，所以，这个原则是正确的。但一定要注意，这个“所有”和“都”，不能部分地被代替，那样就错了。

这些规律、原则是很有用的。可用以化简逻辑表达式。对应电路、梯形图，就可用最少触点、指令，去表达相同的逻辑关系。

提示：本书第1章中图1-1及图1-2中若干功能相同的电路都可运用上述规律、原则予以证明。

（4）触点电路范式。从工艺与使用上考虑，触点电路应标准化。使用PLC的指令也有这个问题。标准化的触点电路称触点连接标准型，也称范式。有两种范式：合取范式与析取范式。

1）合取范式。它是由一些析取范式的合取，是先加后乘的逻辑式。其对应的电路是先并、后串。如表达式

（X+Y）∗（Y+Z）∗（Z+X）

即为合取范式。

容易证明，任一触点电路的逻辑式，运用上面讲的规律、原则作一变换，总可以化为合取范式。如表达式：

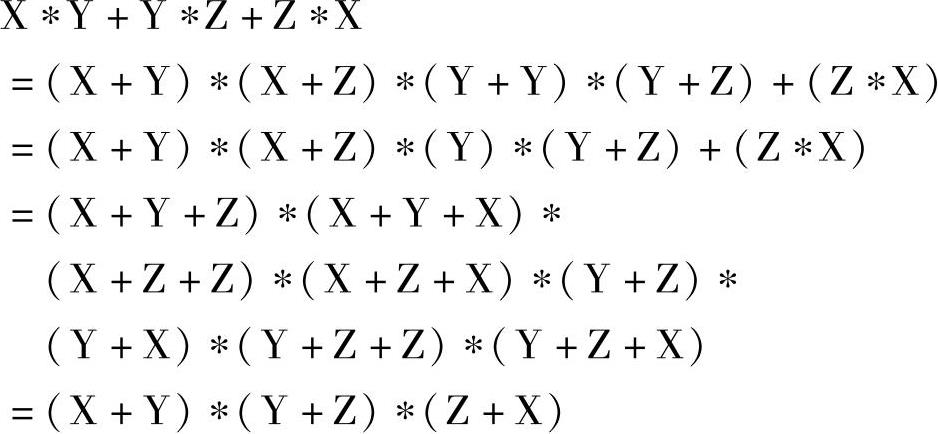
这里用了分配律作变换，把不是析取范式变换成合取范式了。也可运用反演律求解。其结果也是一样的。

运用合取范式很容易求出代数式为零的条件。如上式，只要在3个和项中，有一个为零，这个式子的结果即为零。

2）析取范式。它由一些合取范式的析取组成，是先乘后加的式子。其对应的电路是先串、后并。梯形图很常用这个范式。如表达式

X∗Y+Y∗Z+Z∗X(www.xing528.com)

即为析取范式。

也容易证明，任何一个触点电路的逻辑式，运用上面讲的规律、原则作变换，总可以化为析取范式。如

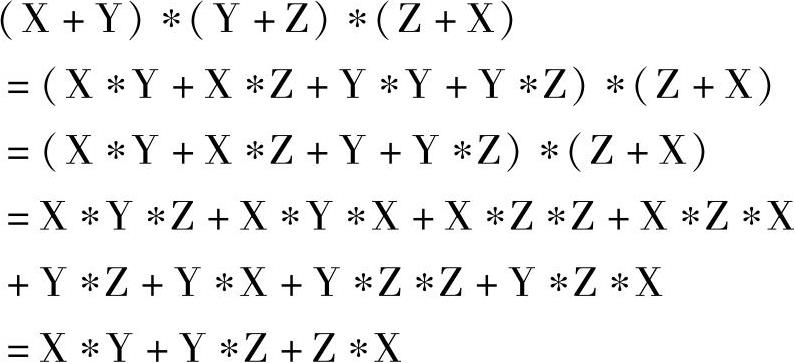
这里用了分配律、吸收律、结合律等作了变换，把合取范式变成了析取范式。也可运用反演律求解。其结果也是一样的。

用析取范式很容易求出逻辑式为1的条件，如上式，只要在3个乘积项中，有一个为1，这个式子即为1。

应该指出，范式虽是标准型的触点连接，但它不是惟一的。逻辑化简，就是要寻找最简的范式，即寻找能实现所要求的功能而又是标准化型触点连接的、且用的触点又是最少的逻辑式子。这对PLC讲，就是用最少的指令，去实现所要求的功能。

（5）触点电路特异范式。由于范式不是惟一的，不大好把握它，为此再介绍一下特异范式。

1）1的组分。1作为逻辑量，可用下式表达，即

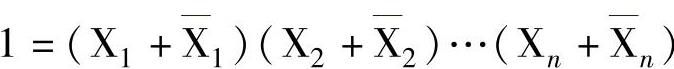
根据分配律，可把上式的右边展开成析取范式，共2的n次方项，即

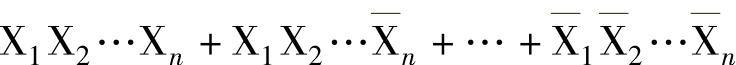
若把以上乘积项中，X_i看成1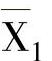，看成0，则其每一项均可看成是一个二进制的数。然后再对应地译成十进制数，则有

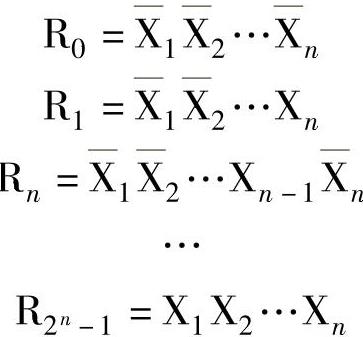
这样，表达1的式子可写成

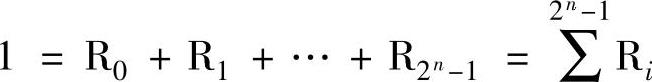
这里的R_i就叫做1的组分，1是由它的所有组分的析取而成。

显然，1的组分要随所讨论的变量多少而变化。当变量数确定后，它的组分是确定的。

可以证明，任何一个触点电路，除恒不通外，表达它的触点逻辑式总可以展开成若干1的组分的合取。如

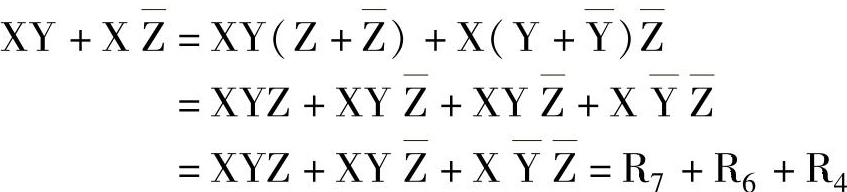
1的组分又称最小项目，上式有3个1的组分，即说它包含了3个最小项。

最小项表达的逻辑式子又叫特异析取式。显然，对一个具体的电路，变量数确定之后，特异析取式是惟一的。

与1分解为n个变量的组分的析取相对应的电路叫触点塔。图3-18所示为3个变量的触点塔。

从图知，不管X、Y、Z怎么搭接，A点总有一条路通到下面来。

这个触点塔有3层，因为它含有3个变量。由此可以推知，触点塔的层数总是等于它所含的变量数。

因为任何一个触点电路，总可以用1的若干组分的析取表达，所以，它也总可以看成是1的触点塔的某一部分。反之，有目的地取出1的触点塔的一部分，总可以构成满足一定要求的电路。

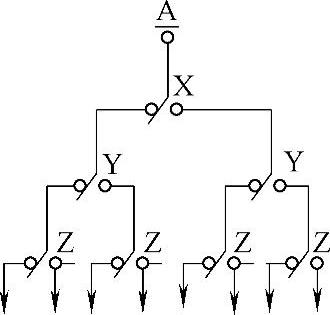
图3-18 三个变量的触点塔

2）0的组分。与1的组分相对应的，还有0的组分。根据反演律，有

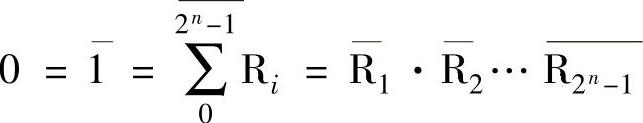
其中R_i可展开成和的式子，并称之为0的组分。如n=2，则

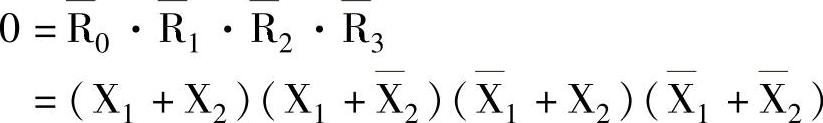
其对应的电路如图3-19所示。它为多节构成的，n个变量有2ⁿ个节，每节有n个节点并联。从图可看出，不管怎么搭接，A到B总是断的。这正好与它用来表达0相对应。

图3-19 多节构成电路

也可证明，任何触点电路，除为恒通外，均可以变换成若干0组分的合取。这个合取式也称该电路的特异合取式。显然，对任一具体电路，变量数一定时，表达它的特异合取式是惟一的。

既然任一具体电路可表达成特异合取式，那么，取出0电路的一部分（即去掉若干节），只要它符合特异合取式，则它也完全可实现具体电路的功能。

两种特异式子可按一定规律进行转换。具体是，特异合取式是0的组分先减去要转换的特异析取式的所有项，再把余下的各项分别取非，然后再合取；特异析取式是1的组分先减去要转换特异合取式的所有的项，再把余下的各项分别取非，然后再析取。如特异析取式

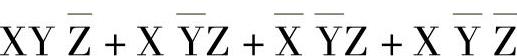
求其等效特异合取式，可：先求1的组分，再减去上式中所含的1组分，余下的为

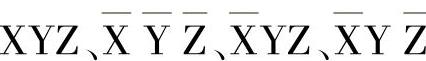
对这四项再分别取非，各为

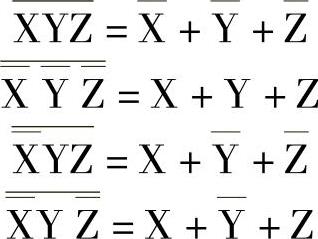
以上四项的积，即为这里所求的特异合取式，即

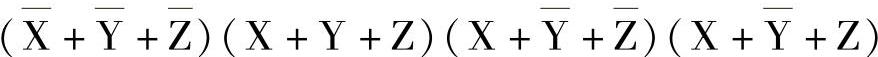
反之，也可倒推回去，其推导过程略。

从以上介绍可知，变量数定了之后，对任一电路，表达它的特异范式总是确定的、惟一的。而且两种特异范式可以互相转换。特异范式用的触点多，实际上不用它，但可说明使用触点最多时的情况，对把握与理解电路是很有用的。

（6）多输出触点电路及其数学表达式。以上讨论触点电路都只有一个输出值，是单输出触点电路。实际电路有时要求同时有多个输出变量，如要对多个对象控制，就要用到多输出触点的电路。若用数学表达式表示多输出触点的电路，则为一组表达式，表达式的右边不仅无自身变量，而且也无其它输出变量。具体如下：

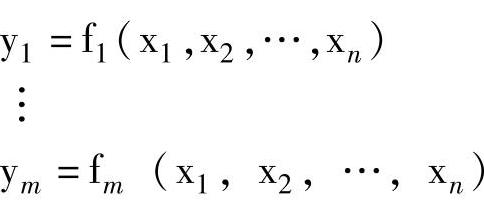
这里有n个输入，即x₁，x₂，…，x_n，同时还含有它们的非。m个输出，即y₁，y₂，…，y_m，同时还含有它们的非。对应的有m个表达式。图3-20表示的组合逻辑的入出关系。

上述表达式也称为组合逻辑的一般表达式。

多输出电路的化简可先分别对各个输出的表达式进行化简，然后再作输入触点兼用“合并”处理，以求在总体上用最少的输入触点，实现多触点输出。有关多输出触点电路化简详细介绍可参阅有关多输出组合逻辑的专著。

2.真值表

真值表是由行与列组成，用以记录输入变量与输出间的对应关系。它的“列”记录着变量的不同取值；“行”记录着输入变量不同取值时，输出的取值。表中1代表器件工作，常开触点ON，常闭触点OFF；0代表器件不工作，常闭触点ON，常开触点OFF。

如表3-2，就是反映A、B两个输入变量不同取值时，它对应的输出，做不同逻辑运算后的值。

提示：真值表的输入一般应涵盖所有的可能，但顺序可任意。

图3-20 组合逻辑的入出关系