【摘要】:I/O分配除了考虑实现算法的方便,还要考虑硬件接线,及防止输入信号受干扰。从图知,它就是实现欧几里德算法中,在花括弧内的算法。直到200.02 ON,并通过200.03使200.01OFF,不再调用子程序。提示:图2-132程序用了微分指令及200.01的自保持功能,目的是确保在200.02OFF,即y未能被x整除时,子程序一直在调用。
算法表示的方法较多。凡能表达出算法思想、步骤,而又能让人理解的方法,都可使用。本节开始介绍的求自然数xx,yy公因数的欧几里德算法,就是用符号语言表达的。此外,还可用图解表达、图表表达及文字说明表达。
1.图解表达
图2-130所示的为xx、yy两个数的公因数的求解算法。图中方块表示“运算”,菱形表示“判断”,连线及其箭头表示“步骤及其联系”。
从图可知,这个表达是可清晰地反映上述求解过程的。
2.图表表达
表2-25所示的为上述算法的求解图表。该表列了5个步骤。第1步为求解开始,进行求“余数计算”。第2步为“判断”,根据判断结果分成2个走向,或求解结束,或继续求解。显然这个图表也可清晰地反映上述求解过程。
3.文字表达(https://www.xing528.com)
上述算法也可用文字表达。可做如下表达:当求解开始后,先是求yy被xx整除,并把余数存于zz中。然后判断zz是否为0?如等于0,则xx即为公因数,运算结束;如不等于0,则xx赋值给yy,zz赋值给xx,并重复开始的步骤。
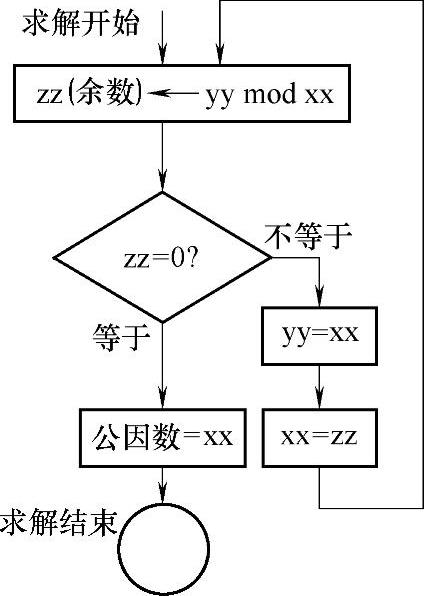
图2-130 算法图解表达
表2-25 求解图表

显然,文字表达是不够精炼的,特别是求解的问题较复杂时,更难以让人理解。故本书用的算法表达多是图解,或表格。个别也用一些解析式子。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




