弹载相控阵探测器高分辨成像实验

将待测区域沿着距离向进行拓展，形成待测目标区域，用于进行目标区域的高分辨成像实验。由图6-13提取出另一块区域散射系数数据作为探测初始数据（详见附录B），利用仿真得到的天线方向图形成回波数据，再对每一散射单元的回波数据增加相应的地杂波数据。

地杂波与目标反射回波被探测器接收天线截获，作为弹载相控阵探测器信号处理单元的输入，经过方位向测角与距离向定距，最终得到探测区域的高分辨方位-距离像。目标区域中随机产生多个强散射目标点（仿真实验中随机生成20个强散射目标点），且令强散射点的实际高度与散射系数成正比，根据回波信号获取目标区域不同强散射点的距离信息，仿真结果如图6-18所示。

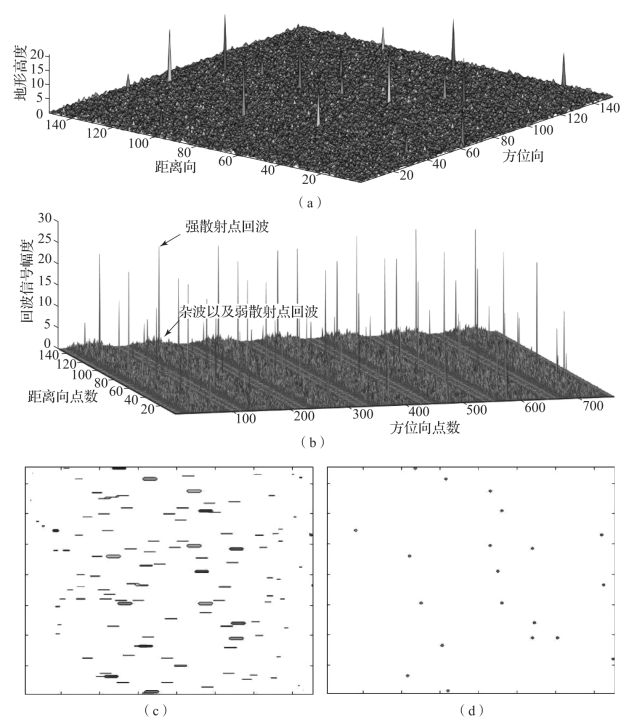
图6-18　20个强散射点的高分辨成像结果

（a）待测目标区域强散射点设置（20个强散射点）；（b）各阵元截获的回波信号数据；
（c）聚焦前成像结果；（d）聚焦后成像结果

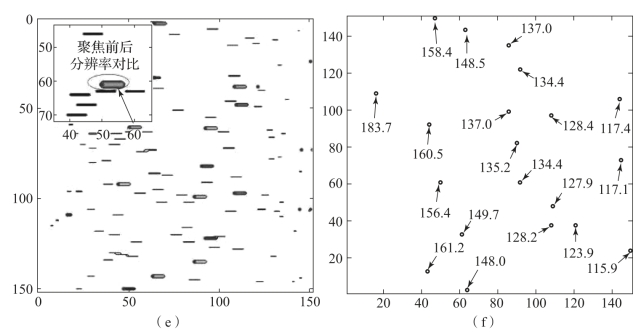
图6-18　20个强散射点的高分辨成像结果（续）

（e）聚焦前后方位向分辨率对比；（f）高分辨方位-距离像结果

如图6-18所示，利用高分辨成像算法对目标区域内的20个强散射点目标进行成像。图6-18（b）显示了各个截获阵元针对不同距离维的目标区域扫描后得到的回波信号数据，根据回波数据进一步得到前视高分辨强散射点成像结果。与理论推导相同，经过方位向的聚焦算法处理后，散射点在方位向上相比于未聚焦时覆盖的区域更小，更接近于冲激响应，提升了成像分辨率。体现在最终的成像结果中，聚焦后的强散射点图像并没有较大的方位向覆盖范围类似点目标像，如图6-18（e）中的聚焦前后分辨率对比放大图。图6-18（f）显示了经过自聚焦后的高分辨方位-距离像，根据高分辨测距算法求解获得每一强散射点与弹载探测器天线之间的距离，分别对应不同的散射点。利用蒙特卡洛重复实验验证高分辨成像算法的边界条件以及探测精度，具体仿真结果如图6-19所示。(www.xing528.com)

将高分辨成像算法中的测角过程应用不同的测角算法，在不同的SNR条件下分别对目标区域内的20、30个强散射点进行蒙特卡洛分析，得到最终的定距误差。

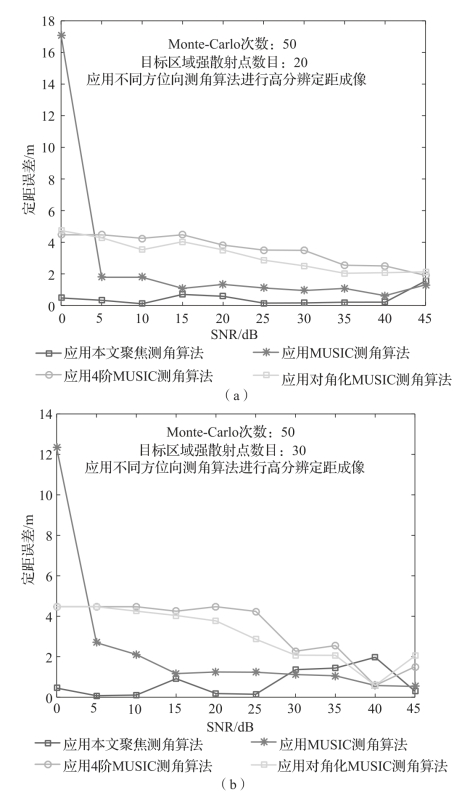
图6-19　不同高分辨成像算法误差对比结果

（a）不同测角算法获得的方位-距离像（强散射点＝20）；
（b）不同测角算法获得的方位-距离像（强散射点＝30）

由误差曲线可以看出：应用本章提出的方位向聚焦测角算法进行成像时，误差处于较低值；而传统的MUSIC及其相应的优化测角算法的最终误差较高，结合MUSIC测角算法的误差最高可达17 m，这是由于信噪比较低无法进行有效的矩阵估计造成的，可将信噪比为0 dB的MUSIC测角算法结果视为无效点。三种MUSIC算法最终的估计误差约为4 m，且在较多的强散射点目标区域探测的过程中，结合MUSIC测角算法的误差曲线波动较大。综上，基于自聚焦的高分辨成像算法更适用于弹载相控阵探测器。

针对目标区域强散射点高分辨成像问题，本章提出了基于自聚焦的弹载探测器前视高分辨成像算法。首先对成像仿真地杂波环境进行建模分析，利用无人机搭载平面探测器对目标区域地杂波数据进行采集，划分波束覆盖区域散射单元后，针对每一散射单元建立杂波环境用于仿真实验；然后分析弹载相控阵探测器高分辨成像原理，提出成像方法以及算法实施步骤，并针对成像方法的各步骤的耗时进行分析，同时针对相应算法耗时问题提出改进措施；最后在仿真实验中，利用成像方法对单一目标与目标区域进行仿真。

仿真结果表明：

（1）对目标区域的成像算法的平均整体耗时小于1 ms，且不同相位调制范围对于距离像精度会产生影响，当调制范围达到［-π／3，π／3］后，随机相位调制范围进一步扩大会对算法响应耗时产生负面影响，因此在实际算法应用过程中，调制范围为［-π／3，π／3］。

（2）仿真实验验证了算法的可行性，将定距结果与实际距离相比较，定距结果与实际距离之间的误差不超过1 m，同时对每一散射点的轴偏角估计误差不超过0.8°。