弹载相控阵前视测距模型研究

针对提出弹载探测器的前视定距问题，提出一种基于分步脉压的弹载探测器测距算法。首先建立弹载探测器测距模型，如图5-5所示。

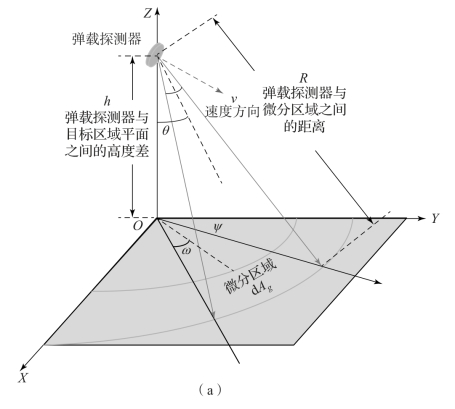
图5-5　弹载探测器测距模型

（a）探测模型

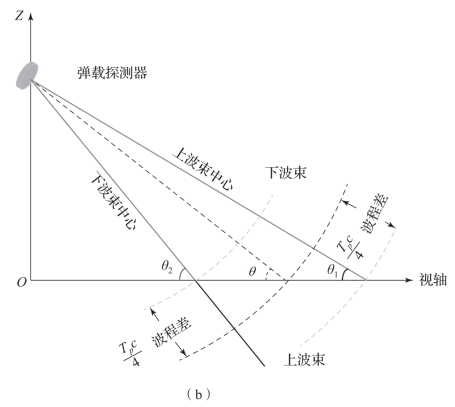
图5-5　弹载探测器测距模型（续）

（b）视轴“切面”模型

图5-5（a）中，ω为两波瓣中轴与视轴之间的夹角；ψ为视轴与Y轴之间的夹角；θ为视轴与Z轴之间的夹角；h为弹载探测器高度。图5-5（b）是图5-5（a）沿视轴方向的“切片”模型，即以Z轴与视轴在XOY平面的投影为坐标轴建立的。

在弹载相控阵探测器开始工作后，辐射天线方向图由上、下波瓣组成，两波瓣在高度上小角度地位移，距离载弹R处的探测区域的功率密度可以表示为

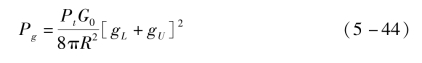
式中，Pg为目标区域功率密度；Pt为发射功率；R为探测器天线与目标区域间的距离；G0为发射天线增益；gU、gL分别为相邻两脉冲方向图函数。取探测区域内一小区域的功率密度函数可以表示为

式中，σ0为微分区域的后向散射系数；dAg为微分面积。如图5-5所示，则式（5-44）中微分区域可以表示为

则利用式（5-44）～式（5-46）可以获得和、差回波功率的微分表达形式：

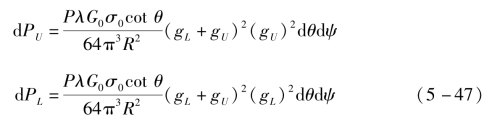
式中，λ为发射信号波长；P为辐射功率，当且仅当除去脉冲持续时间内P＝P0，否则为0：

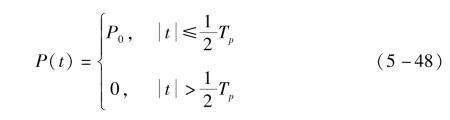
式中，Tp为脉冲持续时间。如图5-5（b）所示，上下波瓣与地面所成夹角即为θ的上下限，则θ1与θ2可以表示为

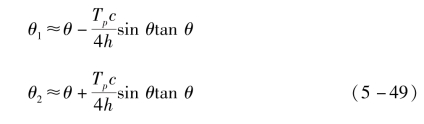
式中，c为电磁波传播速度。(www.xing528.com)

则可以利用上述推导，得到探测区域的回波和、差通道总功率：

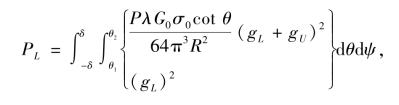
式中，δ为ψ的上下限，由弹载探测器本身决定。δ就是探测波束视轴与飞行方向的最大角度。通常相邻两脉冲信号可以表示为

式中，系数、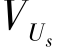均由雷达参数和回波信号的区域的散射特性决定。而在实际的工程实践过程中，单脉冲发射信号由Bessel二阶函数进行构建。则和、差信号可以表示为

和、差信道的回波信号经过相位检波器后，当且仅当两信号的相位正交时，输出为0。例如：当和、差信号相位相差90°时，即

对式（5-53）左右两边同时取正切函数，得

则有

结合式（5-53），式（5-55）的左边为下波瓣脉冲功率，右边为上波瓣脉冲功率。则可得当上下探测脉冲回波信号的功率相同时，相位检波器输出为0，此时对应的斜距离即为弹载探测器与目标区域的视轴距离，即当

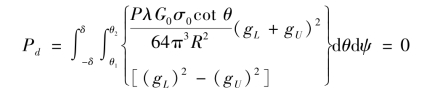
时，对应的R即为所求载弹与目标区域的斜距离。在同一距离维进行扫描，即可获得该区域的斜距离向量（根据方位分辨率的不同，向量的规模不同），实现载弹对前视区域的有效测量。对于脉冲信号，利用二阶Bessel函数进行建立，可以表示为

式中，J2为Bessel二阶函数；α为上下波瓣与波束视轴的偏移角度；G0为天线增益；W为波束宽度。通过式（5-56）可以计算任意角度条件下的上、下瓣时域函数；相应的和、差信号功率可以通过式（5-50）积分得到。将式（5-56）代入式（5-50）中，可得和、差通道信号功率为

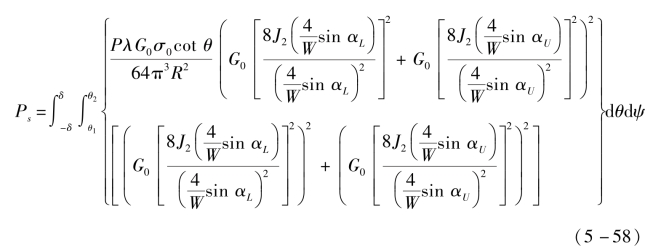
在不考虑回波信号多普勒频移、接收机噪声以及杂波的情况下，利用式（5-57）、式（5-58）即可解算获得某一时刻探测器天线与目标区域强散射点之间的距离信息。