验证AOMRC-AMA测角精度的时频算法对比实验

相比于时频测角算法，如MUSIC、单源点检测等，AOMRC-AMA的迭代过程不具备复杂的计算过程；相比于传统的测角算法，AOMRCAMA具备良好的计算效率，将传统的时频测角算法与AOMRC-AMA对比，以验证不同算法对于相同的目标环境的测角误差，同时对比不同算法之间的响应耗时。待测区域内设置两个强散射目标，运用上述不同的测角算法在不同的SNR条件下进行蒙特卡洛分析，每一SNR条件下进行50次Monte-Carlo计算，得到测角误差，如图4-13所示。

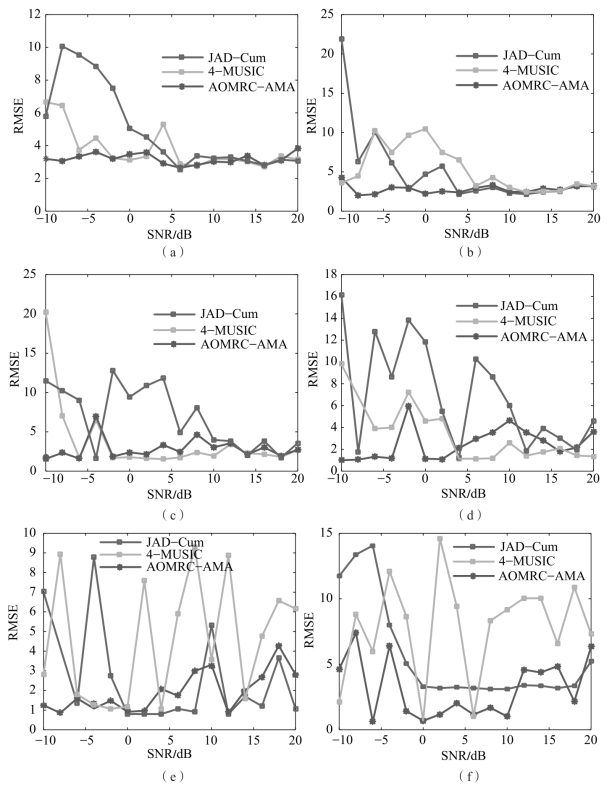
图4-13　SNR为-10～20 dB条件下JAD-Cum、4-MUSIC、AOMRC-AMA测角误差对比

（a）散射点角度　［-3°，3°］；（b）散射点角度［-2°，2°］；
（c）散射点角度［-1.5°，1.5°］；（d）散射点角度　［-1°，1°］；
（e）散射点角度［-0.8°，0.8°］；（f）散射点角度［-0.5°，0.5°］

三种不同的测角方法（JAD-Cum、4-MUSIC、AOMRC-AMA）在-10～20 dB的SNR范围内对两个不同夹角的散射点进行角度测量。由于两散射点之间的夹角变化，测角误差逐渐提升。如图4-13（e）、（f）所示，当两散射点之间夹角缩小后，不同测角算法所呈现的测角误差相较于夹角较大的两散射点的目标区域更加不稳定，尤其是4阶MUSIC测角算法，随着SNR的改变测角误差振荡剧烈，显得极其不稳定。AOMRCAMA测角误差依旧处于三种测角算法误差的低点，在一定程度上说明了AOMRC-AMA测角的优越性。

但是随着两散射点之间的夹角逐渐缩小，AOMRC-AMA测角误差会产生振荡。造成这种误差振荡现象的原因包括：①蒙特卡洛仿真次数过少；②AOMRC-AMA测角过程迭代次数限制；③探测信号波束宽度。因此在实际测角过程中需要改进探测波束参数，同时也要对迭代次数（即仿真阈值）进行约束。JAD-Cum算法在上述实验中的振荡范围最大，且在两散射点之间的角度相距较大时，在SNR处于-10～0 dB范围内的测角误差达到了6 dB以上，最大值为10 dB，导致测角误差无法满足预设要求。但JAD-Cum算法能够在SNR大于5 dB时，使测角误差满足预设要求，测角误差小于4 dB。(www.xing528.com)

随着两散射点之间的角度接近，JAD-Cum算法的误差振荡逐渐增加，振荡值最大为7 dB，因此该算法的测角很难适用于实际的探测过程。4-MUSIC测角算法也具有与JAD-Cum算法类似的振荡测角误差。同时，上述两种空时自适应测角算法的数学推导中，包含了较多的复杂数学计算模式以及循环，影响了算法的整体响应耗时，导致实时性降低。

针对弹载相控阵探测器前视高分辨测角问题，提出一种基于自适应最优单脉冲响应曲线的高分辨测角算法。本章建立了弹载相控阵探测器前视高分辨测角模型，对弹载探测器前视高分辨测角的影响因素进行分析，同时研究了由信号接收通道噪声以及单脉冲响应曲线造成的测角误差，在此基础上提出了高分辨测角算法。利用不同的仿真实验与实验室测试，对AOMRC-AMA的可行性与优越性进行验证。

仿真结果表明：

（1）测角误差分析说明MRC会在回波信号处理过程中对方位向测角分辨率造成较大影响，当MRC逐渐趋近于OMRC时，方位向测角结果逐渐实现“聚焦”。

（2）从单一目标的测角结果可得：MRC的准确程度直接影响目标区域强散射点的角度测量，最终的测角聚焦程度受不同k值条件下MRC的制约，说明了求解OMRC对于前视测角分辨率的提升的必然作用，应用高分辨测角算法，方位向的分辨率约为传统波束扫描测角的10倍。

（3）从高分辨测角实验与算法对比实验可得：AOMRC-AMA在测角精度以及分辨率方面具备优越性，当两散射点在方位向逐步接近，AOMRC-AMA依然能够具备一定的方位向高分辨，说明了该算法相比于传统的时频测角算法具备更大的适用范围。