正则化匹配追踪算法的重构矩阵理论推导

为解决上述病态问题以求解目标区域散射矩阵，利用相关正则化算法对欠定方程进行有效求解，以获得散射矩阵各元素的精确解。弹载探测器的高分辨率成像面临着巨大的挑战：一是探测器在现有的条件下难以实现较高的信号采样频率；二是受探测器规模的限制，难以在带宽限制的条件下实现实时的回波信号处理［41］。结合压缩感知（Compressive Sensing，CS）理论，在SAMP（Sparsity Adaptive Matching Pursuit，稀疏度自适应匹配追踪）重构算法的基础上，设置自适应迭代步长，提升重构算法的收敛速度。

压缩感知理论充分运用信号稀疏度估计来处理观测矩阵，实现源信号准确估计［42］。相关重构算法是CS理论的关键技术，包括贪婪算法、正交匹配追踪（Orthogonal Matching Pursuit，OMP）算法［43］、正则化正交匹配（Regularized Orthogonal Matching Pursuit，ROMP）算法［44］、子空间追踪（Subspace Pursuit，SP）算法等，上述算法在信号重构的过程中，必须以观测矩阵稀疏度为先验知识才能有效实现源信号准确估计。但是在实际探测过程中，待探测区域内的目标散射系数矩阵的稀疏度无法事先得到，因此稀疏度不能作为先验知识，传统的正则化算法对目标矩阵的重构精度将会大幅降低。基于此，SAMP算法［45］被提出，能够在没有稀疏度先验知识的条件下对源信号进行重构。

按照弹载探测器前视成像的回波信号形成模型与稀疏重构模型具备天然的一致性，若充分利用回波信号的稀疏性的先验知识，能够进一步提升目标区域内的强散射点成像精度。发射信号经过目标区域内的强散射目标后，反射形成回波信号被天线截获，则被截获的回波信号即为观测信号数据，而发射信号为投影矩阵。利用相关正则化算法即可求取目标区域强散射点的唯一解，实现脉冲波束内的高分辨。如式（2-24）所示，对于弹载探测器而言，y为M×1维的观测矩阵；x为目标区域N×1维的散射点系数矩阵，且x为稀疏矩阵；H为M×N维的变换矩阵。可分别表示为

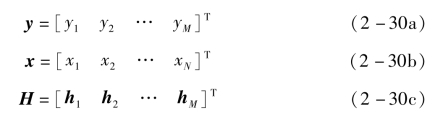
式（2-30c）中，hi为第i个阵元波束方向图向量（1×N维）。对于SAMP重构算法的具体流程是根据残差迭代，对目标散射点系数矩阵的稀疏度进行逐渐逼近，从而最终实现信号矩阵准确重构。当SAMP算法对待重构目标信号矩阵稀疏度进行估计时，必须满足有限等距性质（Restricted Isometry Property，RIP）条件，即：

当矩阵H以参数（K，δK）满足RIP条件时，其中K为x的真实稀疏度，若K0≥K，有

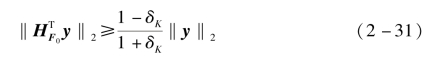
式中，K0为估计的初始稀疏度；F0为H中与残差最匹配的K0个元素对应的索引集合；HF0为H中对应索引集F0的元素集合。

在传统的SAMP算法中，需要首先对待重构矩阵的稀疏度进行估计，从而利用稀疏度作为先验知识用于信号重构。在对稀疏度进行估计的过程中，若设置初始稀疏度为1或阶段步长取较小值，步长较小时则需要更多次的匹配、更新、信号估计以及残差更新等步骤，估计精度提高的同时却降低了算法的整体效率；若初始稀疏度设置较大或步长取值较大，算法的整体效率会得到提升，但是估计精度会受到影响。因此，运用传统的SAMP算法对于前视目标区域强散射点的散射系数矩阵进行重构时，必须通过先验知识或具体计算得到较为准确的初始稀疏度以及更新补偿，使得重构精度与算法的整体实时性同时满足弹载平台预设要求。

为此，提出一种改进的自适应变步长正则化信号重构算法，每次迭代计算首先确定残差r，然后根据选择的观测矩阵中各元素与残差最匹配元素，得到二者的相关系数，表示为

式中，〈〉为相关函数。令r0为初始迭代残差，可表示为

(www.xing528.com)

式中，为散射点系数矩阵估计值，可表示为

式中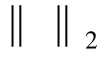，为二范数。每次迭代过程中均采用最小二乘法进行信号残差更新，得

式中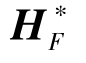，为HF的伪逆矩阵。在某一迭代过程中，支撑集F的大小保持不变，利用式（2-33）求取测量矩阵的各元素与残差的相关系数；合并索引集与上一次迭代的支撑集得到候选集，利用残差与候选集中每一元素的内积最大值对应的索引形成当前迭代过程的支撑集F*。当计算残差的二范数小于上一次迭代过程中的残差二范数时继续进行迭代计算，否则进入下一阶段，当残差的二范数小于预设阈值时停止迭代。SAMP算法［46］就是根据对残差的不断更新来实现对目标信号的准确重构且目标信号的稀疏度未知。当满足RIP条件时，待测的稀疏信号就能够被重构，同时在重构初期也可不需要利用信号稀疏度作为算法的先验知识，重构算法利用控制步长迭代实现对待重构信号的稀疏度逼近。

SAMP重构算法的步骤如表2-1所示。

表2-1　SAMP重构算法的步骤

续表

由表2-1可以看出，传统的SAMP稀疏信号重构算法每一次的迭代步长随迭代次数增加而增加，迭代后得到的最终支撑集长度即被视为重构信号的最终稀疏度。当迭代步长较大时，可以保证算法的收敛速度，但对于算法精度却十分不利；当步长取值较小时，迭代次数会增多，算法的整体效率较低，但是对于待重构信号的稀疏度估计，算法的估计精度会得到提升。

因此，SAMP算法的重构精度与重构效率受到步长和初始稀疏度估计值的影响较大，综合考虑算法的初始稀疏度以及算法迭代步长，即可同时提升算法最终的估计精度与效率。