基于随机相位调制的发射信号的数学模型优化

相控阵发射天线通过移相器实现每一阵元的初始相位按照固定步长进行调制，从而实现相位控制。因此，相控阵探测器能够通过调整移相器的相位调制方式来实现对每一阵元发射信号的随机调制，通过设置合适的随机相位调制范围，即可在实现高分辨探测的同时兼顾探测过程的整体响应效率。

对相控阵每一阵元发射波形的幅度与相位进行调制，从而使合成的探测波束具备随机相位调制特性，以均匀线阵为例（Uniform Linear Array，ULA），弹载线控阵探测器实现每一发射信号相位调制的具体方法如图2-5所示。

图2-5　ULA的常规探测波束与随机相位调制探测波束

（a）常规探测波束；（b）随机相位调制探测波束

相位调制将改变不同阵元的发射波束的初始相位，因而经过目标反射后由天线截获回波信号中也具备发射信号的随机调制相位。为实现高分辨探测，弹载相控阵探测器的探测波形为线性调频子脉冲频率步进信号，由不同的阵元向外辐射脉冲信号；经过目标区域的强散射点反射后，回波信号依旧携带这些调制信息，且相较于未调制信号探测，由目标反射形成的回波信号拥有更多的目标区域强散射点的有效信息。

按照前文的理论推导，接收天线位置处的目标散射回波可以由Fredholm方程［40］表示：

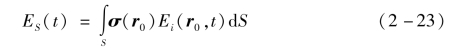
式中，Ei（r0，t）为t时刻r0个散射单元处的探测波束辐射场，则ES（t）为S范围内的所有散射单元回波能量，由不同位置处的散射系数σ（r0）与辐射场Ei（r0，t）乘积的积分获得。

由于单一波束内的辐射场近似均匀分布，从数学求解角度考虑，同一个发射波束只能产生一个有效方程，无法实现波束内的高分辨探测。因此，为实现波束覆盖范围内高分辨就必须为同一波束辐射场赋予更多的独立、正交方程，这就要求在同一波束覆盖的区域内，波束辐射场的内部必须具备时间与空间上的统计独立特性，波束内不同的强散射点就会被差异性分布的辐射场所标度，即存在不同的独立方程来定义不同强散射点的回波信号，以确保散射场的回波中蕴含了所有可辨识的目标空间分布信息。若将高分辨成像视为线性过程，对于线性探测系统可表示为

(www.xing528.com)

式中，y为接收天线截获的目标回波信号矩阵；H为系统的传递矩阵，由探测模型决定；x为目标区域内的散射点矩阵。随机相位调制依靠矩阵H表示，体现在求解x的过程中，发射信号方向图矩阵H的行、列非相关性较强。对式（2-24）中的矩阵H进行描述，有

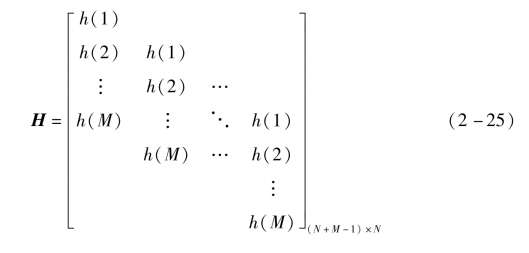
式中，h（1）至h（M）为发射天线方向图采样数据；H为阵列信号的方向图矩阵。因此，已知探测器天线根据目标区域回波信号矩阵y与发射信号方向图矩阵H，求解目标区域的散射点矩阵x。一般而言，用最小二乘解作为x的精确解，则有

对H进行奇异值分解，得

式中，ULS和VLS均为单位正交矩阵，则矩阵D可以表示为

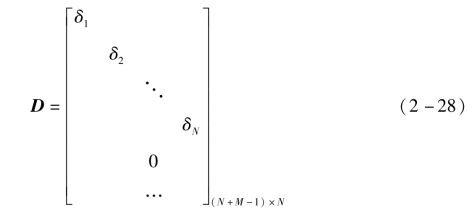
式中，矩阵中的元素δi可以表示为其中λi为HTH的特征值。则由特征值分解可得x的解为

式中，u和v分别为矩阵ULS和VLS的元素。通常情况下，探测器的方向图一般由一系列的Sinc函数叠加组成，此时的δi呈现梯形下降分布且数值跨度较大，即使信噪比很大，也会使求解的xLS与真实解之间相差较大，在高分辨问题中成为病态性，而这种病态性会导致求解的不稳定，因此需要利用相关正则化方法进行求解。