随机相位调制探测原理分析与实现

由平面波分解定理可知［35］：探测信号的任意一种照射模式都能够被视为若干个不同幅度、频率、初相和入射角的均匀平面波的叠加。因此，当相邻阵元之间的发射波束的自由度越高（非相关性越强），探测信号到达待测目标平面后，由目标区域强散射点反射得到的回波信号中所携带的目标的有效信息就会越丰富，进而能在越短的时间内、单次测量过程中获得足够多的目标信息，实现载弹平台高分辨探测。由于毫米波近炸引信的空间限制，相控阵探测器天线阵列规模难以拓展，因此，在探测器天线硬件结构保持不变的前提下，利用随机相位调制实现单次发射波形模式的多样化［36］。相比于传统的毫米波探测系统，随机调相后的发射波束为有限的相控阵天线平面提供了更多样性的辐射模式，极大提升了毫米波探测器高分辨探测能力［37］。探测器的收发链路也较为简单，易实现小型化；同时，电控阵列天线也为相位调制提供了硬件支撑［38］。经过随机相位调制的高分辨探测示意图如图2-1所示。

图2-1　经过随机相位调制的高分辨探测示意图

（a）未调制信号；（b）随机调制信号

图2-1中不同的方格表示不同时刻到达不同距离向的波束方向图，每一小方格表示探测器在方位向与距离向的最小分辨单元，对比两种探测模式，未调制信号在同一距离向上的方向图保持一致；而随机相位调制后，在同一距离向上的波束方向图具有差异性。传统毫米波探测系统向目标区域辐射，如图2-1（a）所示，当强散射点1与强散射点2方位信息不同而距离信息相同时，到达两强散射点的探测信号差异较小，因此对于两散射点的回波信号中具有较小的方位信息，很难对两散射点进行方位向分辨。而随机相位调制使发射信号实现相位信息的随机起伏［图2-1（b）］，因探测波束多样的辐照模式，两强散射点处的回波信号有更大概率产生差异，有利于实现前视高分辨探测。

由目标区域强散射点形成的回波信号被相控阵天线截获，且截获的回波信号由发射信号与目标区域强散射点的散射系数共同决定，当考虑接收天线噪声时，相控阵天线截获目标区域回波信号可以表示为

式中，Sr为回波信号矩阵；S为发射信号矩阵；σ为目标区域强散射点散射系数矩阵；Nr为接收噪声矩阵。由式（2-1）可知，回波信号矩阵Sr与发射信号矩阵S均为相控阵探测器的先验知识，其中：

式（2-3）中，r为成像网格中心的位置向量；且定义发射信号中tN时刻、位于rk网格处的信号S（tN，rK）为(www.xing528.com)

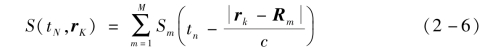
式中，Sm为第m个编码阵元的发射信号；Rm为第m个发射阵元的位置。根据推导，相控阵探测器前视高分辨探测即变成求解式（2-1）的解。理想情况下，式（2-3）中的发射信号矩阵中各行各列相互独立，在无噪声的情况下通过式（2-1）即可利用发射信号逆矩阵精确解算获得目标区域散射系数矩阵σ。但是在现实探测过程中，由于信号带宽、调相范围等因素的影响，发射信号矩阵中必定会存在一定的相关性，因此最终散射系数矩阵的求解必定受到影响。对于传统的前视实波束扫描探测而言，由目标区域各散射点（以2个散射点为例）反射得到的回波信号可以表示为

由于缺乏有效的方程数量，即发射信号矩阵各行、列向量之间存在相关性，发射信号逆矩阵只能利用广义逆矩阵表示，因此由式（2-7）无法得到目标区域σ的精确解，信号处理结果会产生较大的角度误差，进而导致前视成像分辨率较低。而经过随机相位调制后所获得的回波信号可以表示为

式（2-8）中，由于对发射波束进行了随机相位调制，因此辐射到不同散射点的信号之间存在差异，这样就为散射系数矩阵重构带来了可能。推广至多散射点情况，式（2-1）中的发射信号矩阵S的行、列相关性成为对前视多散射点方位向分辨的基础，为求取σ的精确解，需对信号矩阵的秩进行讨论，通常情况下，相控阵探测器信道数目一般比目标区域的强散射点多（即N≥K）：

（1）当rank（S）≥K时，求解σ时的有效方程组数大于待求解未知数，可以通过求解可逆矩阵等方式将向量σ中的各元素进行精确求解。

（2）当rank（S）＜K时，该情况为缺秩情况［39］，在求解σ中各元素时，缺少有效方程组，因此对于某些元素的求解无法得到精确解，且缺秩情况下易受环境因素的干扰，导致目标区域强散射点位置信息很难准确获取。

综上推导，高分辨探测问题最终可以划归成求解式（2-1）中的σ向量的问题。相位调制的目的就是增加不同阵元发射波束之间的非相关性，从而使发射信号矩阵S的行、列非相关性最大，形成类似rank（S）≥K的求解情况，此时的有效方程数量大于未知数个数，因此能够通过常规逆矩阵求解方法得到σ向量的精确解，目标区域内的强散射点即可利用σ向量的所有解来描述。