尺寸链计算公式优化

尺寸链的计算，是指计算封闭环与组成环的基本尺寸、公差及极限偏差之间的关系。计算方法分为极值法和统计(概率)法两类。极值法多用于环数少的尺寸链，统计(概率)法多用于环数多的尺寸链。(下面尺寸链计算公式摘自GB5847—86)

各参数间的关系如图3-9所示。具体可用下式计算。

(1)封闭环的基本尺寸L0。

式中:Li——各组成环的基本尺寸;

m——组成环的环数。

(2)封闭环的中间偏差Δ0(中间偏差即上偏差与下偏差的平均值)。

式中:Δ——组成环的中间偏差，Δi=(ES+EI)，ESi为组成环的上偏差，EIi为组成环的下偏差;

e——组成环的相对不对称系数，它是表征分布曲线不对称程度的系数，e=i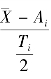，其中Ti为组成环公差，为组成环的平均偏差，即实际偏差的平均值。若组成环在公差带内对称分布时，ei=0，则Δ0=

常见的几种分布曲线相对分布系数k与不对称系数e见表3-7。

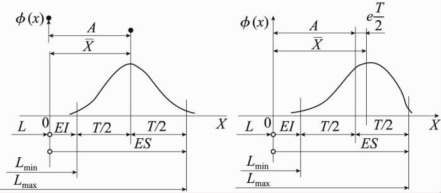
图3-9　尺寸链中各参数间的关系

表3-7　常见的几种分布曲线相对分布系数k与不对称系数e

(3)封闭环的公差T0。

极值公差(www.xing528.com)

统计公差

式中:k——相对分布系数，它是表征尺寸分散性的系数(见表3-7)。正态分布时k=1

(4)封闭环极限偏差。ES0=Δ0+T0　 EI=Δ－T0

式中:ES0——封闭环的上偏差;

EI0——封闭环的下偏差。

(5)封闭环的极限尺寸

式中:ES0——封闭环最大极限尺寸;

EI0——封闭环最小极限尺寸。

对于直线尺寸链，用极值法计算时，封闭环的基本尺寸等于所有增环基本尺寸之和减去所有减环基本尺寸之和。封闭环公差等于所有组成环公差之和;封闭环的上偏差等于所有增环的上偏差之和减去所有减环的下偏差之和，封闭环的下偏差等于所有增环的下偏差之和减去所有减环的上偏差之和;封闭环的最大极限尺寸等于所有增环的最大极限尺寸之和减去所有减环的最小极限尺寸之和;封闭环的最小极限尺寸等于所有增环的最小极限尺寸之和减去所有减环的最大极限尺寸之和。

(6)组成环的平均公差。

①极值公差Tav，L。

②统计公差Tav，S。

(7)组成环极限偏差。

(8)组成环的极限尺寸。