复杂型面加工技巧探究

有些零件轮廓形状，如汽轮机的叶片、挤出机螺杆(或螺套)、空间凸轮和某些锻模、压铸模、塑压模的型腔等，属于空间曲面，这类曲面称之复杂型面。其加工方法主要依赖于其几何构型，主要有仿形加工、数控机床和加工中心机床等加工方法。

以下仅以变螺距螺旋的复杂型面的加工为例来介绍这几种加工方法。

1.4.2.1　变螺距螺杆的仿形车削加工

在橡胶、塑料、食品以及纺织等工业领域所使用的生产设备中广泛地应用着各种类型的挤出螺杆。变距螺杆由于具有压缩均匀、压缩比大、出料连续性好等优点得以优先采用。但由于变距螺杆工艺性较差，利用通用设备加工困难，通过工艺分析，可以利用、挖掘现有通用设备潜力解决此类变螺距螺杆的加工问题。

1.变距螺杆的螺旋线数学方程

变距螺杆是相邻螺距不等的螺杆。常用的变距螺杆螺距变化规律如图1-39所示。

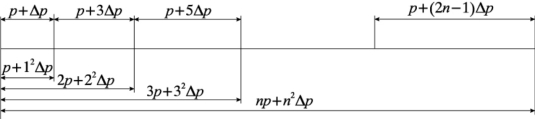
图1-39　变距螺杆示意图

从图中看出，螺杆的螺距是按等差级数规律渐变排列的。若设螺旋曲线上任意点至起始点的距离为l，则可得变距螺杆的螺旋线的数学方程:

l=nP+n2ΔP

式中:P为基本螺距;ΔP为螺距变化量;n为螺旋线圈数，n=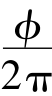，φ为螺旋总转角。

将n=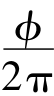代入方程，得

令:A=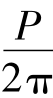，B=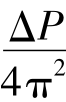，再将φ=ωt代入，则得

l=Aωt+Bω2 t2

式中:ω为螺杆转动的角速度;t为螺杆转过φ角所用的时间。

根据上述方程，对变距螺杆曲线分析如下:

(1)位移分析。

等距螺杆的数学方程仅有变距螺杆方程中的第一项，即

曲线上任一动点轴向位移l与时间t是一次关系，而变距螺杆l与时间t是二次关系。

(2)速度分析。

当螺杆匀速转动时，等距螺杆螺旋线上任意点的轴向速度

式中:A、ω均为常数，故υ为常数，即等距螺旋线上任意动点的轴向位移速度是恒定的。

而变距螺旋线上任意点的轴向速度则说明变速螺旋线上任意动点的轴向速度是时间的函数，是变化的。

(3)加速度分析。

等距螺杆轴向加速度a=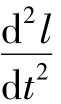=0，变距螺杆轴向加速度a=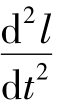=2Bω2，说明等距螺杆螺旋线上任意点轴向加速度为零，而变距螺杆螺旋线上任意点轴向加速度为常数，其速度变化是均匀的。也就是说，变距螺旋线上任意点的轴向位移为匀加(减)速运动。

2.成形运动分析

加工等螺距螺杆，只需主轴带动工件匀速转动，刀具作轴向匀速移动，即可形成等距螺旋线。加工变距螺杆，则一方面须主轴带动工件匀速转动，一方面须刀具作轴向匀加(减)速移动才能形成变距螺旋线:作为通用车床，刀具只能作轴向匀速移动，要刀具作匀加(减)速运动，必须在进给装置中增设能实现匀变速运动的机构。

3.变距加工系统设计

要实现变距螺纹的加工，在成形运动中，要同时实现变距螺纹方程中的Aωt和Bω2 t2两项运动规律。其中Aωt项可由通用车床本身的功能来实现，而Bω2 t2项，则须通过增设一辅助装置来实现。经分析、比较，同时考虑到工艺、结构实施的可能性、经济性及方便性，我们设计了一凸轮机构(辅助进给箱)。利用凸轮的等加(减)速曲线推动丝杠作轴向匀加(减)速运动，便得到了变螺距螺纹的成形轨迹——变螺距螺旋线，如图1-40所示。

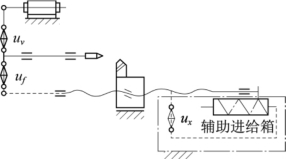
图1-40　变距加工系统原理图

在通用车床丝杠的末端套上一齿轮，通过齿轮将丝杠的旋转运动传递给辅助进给箱中的凸轮。凸轮在转动的同时通过变速曲线推动从动滑板(丝杠轴向固联)，从而推动丝杠相对床身作匀加(减)速运动(丝杠与床身可滑移)。这样，该运动与主轴(带动工件)匀速转动运动合成，即可加工出变距螺杆。

对设计系统的现场加工实例进行检测，数据如下:工件直径D=φ65mm，工件长度L=1900mm，螺纹总长l=1210.95mm，螺纹数n=23，螺距增量ΔP=0.55mm，螺距由40mm渐变至64.75mm，螺距最大误差＜±0.17mm。结果证明，所加工螺纹确为变距螺旋线，符合前面推导的数学方程，即满足设计要求。

4.变距加工系统特点

(1)结构简单、调整方距、经济实用。采用数控机床和专用机床加工变距螺杆的优点是:效率高、精度易于保证;其缺点是:设备复杂、昂贵，工艺成本高等。而该变距加工系统，是利用现有的通用机床，只增加一结构简单、易于调整的辅助进给箱。在加工变距螺纹时，接通辅助进给箱，在进行常规加工时，断开辅助进给箱。这样，不影响机床原有的工艺范围。

(2)变距范围广，产品规格多。加工不同规格的变距螺杆，只需按要求调整辅助进给箱中的挂轮，改变传动比，即可改变刀具匀变速度的大小，因而可加工多种规格的变距螺杆。

(3)产品质量好，生产效率高。用该系统加工变距螺杆，操作简单、质量稳定、生产效率高。

1.4.2.2　变螺距螺杆的简易数控加工

高速供瓶螺杆(见图1-41)是灌装自动生产线上的一个易损零件，它是一种典型的变螺距螺杆，其螺旋线具有与上述变距螺杆类似的数学规律。

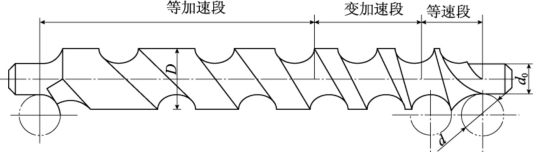
图1-41　高速供瓶螺杆结构

1.加工方法

变距螺杆的螺旋槽轴向剖面的圆弧形状由滚铣刀铣削成形。刀具由普通的滚铣刀经修磨外圆，使它与自动线上的瓶的外径d相等，长度H也等于d。工件与刀具的轴心线相互垂直，轴心距等于瓶(罐)与进瓶螺纹的轴心距，如图1-42所示。这样铣成形的供送螺杆的螺纹槽能与瓶(罐)的外圆很好地吻合。螺旋槽的螺旋轨迹是由简易数控系统控制，使得螺距连续变化，不同的螺距变化只要改变数控系统的程序即可，且不需考虑刀具的干涉。

图1-42　螺杆的铣削加工示意图

2.简易数控系统

(1)硬件部分。可以在通用的51系列的单片单板机上开发这一数控系统。系统框图如图1-43所示，其中前置放大由7404实现;功率驱动为双电源驱动:采用四相四拍的步进电机甲和乙。只要将普通卧铣的分度头手柄处和纵向走刀手柄处分别装上步进电机甲和乙，这样一个两坐标联动的数控铣床就改装完毕，如图1-44所示是一简易数控系统(开环系统)。

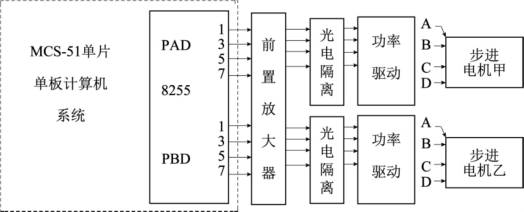
图1-43　控制系统框图

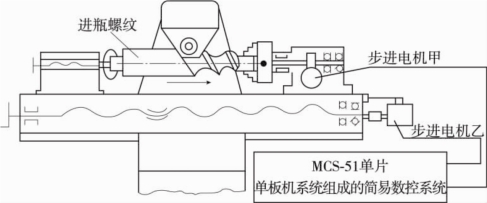
图1-44　简易数控系统(开环系统)

(2)数学模型。圆周方向的匀速圆周运动和轴向的匀速直线运动合运动的轨迹就是一变螺距的螺纹。步进电机甲每次转一个步距角α，经分度头的蜗轮蜗杆传动副(传动比为N)带动被加工的进瓶螺纹转动360N/角α，此时根据进瓶螺纹的起始螺距(或基本螺距)L1、终止螺距L2、螺纹的圈数m、卧铣的纵向丝杠螺母副的螺距T(且假设步进电机乙的步距角也是α)，计算步进电机乙应得到脉冲数P，即旋转P个步距角。另外由于螺距是匀速地增加，每一步的(步进电机甲的每一个步距角)变螺距的增量相等，若n为步进电机甲的总步数，则第k步的变螺距增量为

步进电机甲每旋转一个步距角的基本螺距平均增量h为

(www.xing528.com)

则步进电机乙应得到的脉冲数P，即旋转P个步距角:

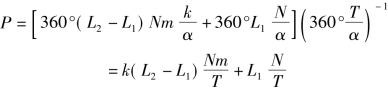
式中:L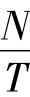——等螺距平均增量脉冲P;

k(L－L)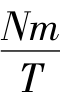——第k步的变螺距增量脉冲P。

数控系统每向步进电机甲发一个脉冲，就只需向步进电机乙发P个脉冲。两个步进电机所产生的运动的合成即为变螺距螺纹的轨迹。

(3)软件部分。由于计算机系统是采用通用的单片单板系统，其中键盘管理、显示、延时等程序可以直接应用(或经简单地修改)原监控程序。8255的PAD和PBD分别控制步进电机甲和步进电机乙。

当数控系统向步进电机甲发一个驱动控制字01H，即转子旋转到A相，由于8255PAD、PBD均具有锁存器，所以就锁定到A相，直到下一个驱动控制字的到来，下一个驱动控制字只要在现在的驱动控制字01H通过累加器A右移两位即04H，B相得电，步进电机甲就旋转一个步距角α;再将PBD的步进电机乙的驱动控制字通过累加器右移2P位，则步进电机乙的转子旋转Pα角，即完成工件的轴向位移。如此类推直到步进电机甲n步走完。

总之，成形和数控相结合的加工方法是一种很好的方法。如加工汽轮机的叶片、塑料机械中的挤出和注射螺杆等都能用这种加工方法。由于有了成形刀具的切削，便得加工效率高且数控系统变得简单，原需三坐标联动的系统，现只需两坐标联动;由于有了数控，所以使得加工的工件比常规加工的质量更好。

1.4.2.3　变螺距螺旋的数控加工方法

双头等加速螺旋轴套是某塑料造粒机挤出杆上的重要零件，螺旋轴套具体形状表现为圆柱状表面上有两条螺旋线，其螺距都随螺线距右端部的距离而作等加速变化，而且螺线都由形式变化的五段组成，是一条螺旋曲面，形状特别复杂，且尺寸精度要求高，这样复杂的曲面采用普通加工方式难以完成，而在数控机床上则相对容易实现复杂曲面的加工。数控加工方式加工出来的螺旋曲面精度高，一致性好，表面只需经过钳工适当的修挫和抛光即可。

以下简单介绍该零件在MITSUBISHI(三菱)MCV-1700加工中心机床上的加工过程。首先，建立数学模型。通过求导，进行数学计算，计算机一维搜索确定拐点，将复杂连续的离散为若干刀位控制点，进一步拟合得到连续的曲线，以实现连续控制。然后，基于这样一个数学模型，编制出NC程序，利用加工中心机床的四轴联动功能加工螺旋轴线。

1.螺旋的数学模型与有关数值分析

(1)数学模型的建立。

螺旋线符合方程:

X=1/2×(A/360)2+227.85×(A/360)A≤1177.955

X=0.55149×(A－1177.955)+861.7143 A≥1177.955

式中:X——螺旋线中心距零件右端的距离，mm

A——螺旋线沿柱面展开角度，°。

将螺旋轴套沿柱面展开，如图1-45所示，在拐点a到b处，螺旋线宽度由22mm变为34mm;在拐点c到d处，螺旋线宽度由34mm变为45mm。假定螺线宽度为零，刀具直径为零，则对应任意A有

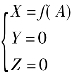
图1-45所示为其中一条螺旋线1，5为刀具中心轨迹;2为R30圆弧所在的螺线边沿;3为螺旋线中心;4为R16圆弧所在的螺线边沿。

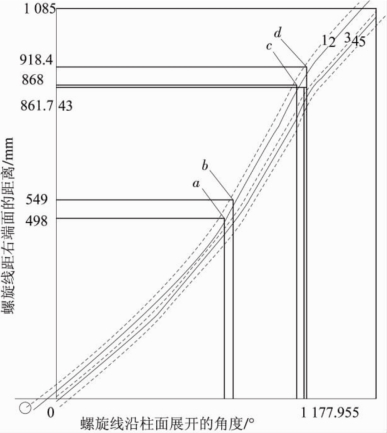
图1-45　螺旋线展开图

(2)刀具补偿量的确定。

考虑螺线宽度及刀具半径，刀具轨迹上任意点为:X1=f(A)+ΔX，即刀具轨迹上的点与螺线中心上的点存在一一对应关系。只要以螺线中心上的点为映射原点，在其坐标值X、Y、Z的基础上增加一补偿量，即可得刀具轨迹上对应点的坐标。以A为变量，计算铣刀中心轨迹，则有

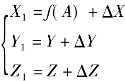
X方向补偿量:ΔX=(R+H+M)×cos［arctan(K)］

Y方向补偿量:ΔY=(R+H+M)×sin［arctan(K)］

Z方向补偿量ΔZ=R+R1－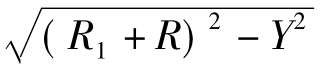

式中:R为球刀半径;H为齿宽;M为余量;K为该点斜率，K=f'(A)，K值等于曲线上该点的一阶导数;R1为工件半径。

(3)有关数值分析。

a点的映射原点为a1，根据我们建立的数学模型，a、a1存在如下的对应关系，过a1作切线A1B1，切线斜率为K，K=f'(A)=df(A1)/dA，K值为曲线在该点的一阶导数，铣刀中心位于a2点，a2a1⊥A1B1。

球刀中心坐标:Xa=Xa1+ΔX Xa1=10.85×(A1/360)2+227.85/360 ΔX=(R+H+M)×cos［arctan(K)］

式中:R为球刀半径，R=0;H为齿宽，H=22/2;M为余量，M=0;K为该点斜率。

运用Quick BASIC程序，确定搜索区间，选择合适的步长，多次进行一维搜索，可得a点对应的A值。Aa1=706.8487，Ab1=755.5609;Ac1=1157.78;Ad1=1219.09。

(4)曲面拟合计算

由于没有R30的铣刀，R30的圆弧面需要用较小半径的铣刀拟合出来，球刀在任意位置。

M=R－R(R－r)cosθ

ΔZ1=－R sinθ+1.5

式中:R为工件圆弧半径，R=30;r为球刀半径;ΔZ1为Z向补偿量;M为余量。

2.数控程序

根据以上的分析及计算，采用参数方式编制数控加工程序，程序包括3部分:①R30圆弧所在曲面的加工程序;②R16圆弧所在曲面的加工程序;③两条螺旋线中间部分铣削的加工程序。(数控程序从略)

习题与思考题

1.零件上的典型平面有哪几种?有何技术要求?试分析不同精度的平面的加工方案。

2.平面的加工方法有哪些?分别采用什么机床来加工?

3.精铣平面时，采取什么措施可提高平面的加工精度?

4.零件的外圆表面有何技术要求?试分析不同精度的外圆表面所采用的加工方案。

5.外圆表面的加工方法有哪些?分别采用什么机床来加工?

6.分别采取哪些措施可以提高外圆车削和磨削加工的生产率?

7.细长轴外圆表面的加工与一般外圆面的加工有何不同?采取哪些措施可以提高其加工精度?

8.简述外圆表面的精密加工方法及特点。

9.零件的内孔表面有何技术要求?试分析不同精度的内孔表面所采用的加工方案。

10.内孔表面的加工方法有哪些?常用的加工设备有哪些?

11.内孔的磨削加工有什么特点?珩磨与一般磨削内孔有什么不同?

12.试总结各种内孔加工方法的特点及其适应性。

13.孔系加工方法有哪几种?试举例说明各加工方法的特点及其适应性。

14.用浮动镗刀加工箱体孔有什么好处?它能否提高孔的相互位置精度?为什么?

15.对不同精度的圆柱齿轮，其齿形加工方案应如何选择?

16.简述各种齿形加工方法的特点及其精度等级。