抽样误差是说明样本指标与全及总体指标之间的离差的平均数。抽样误差说明的只是一个可能范围。例如,在10000个灯泡中进行的抽样检测,检测结果是平均使用寿命为x=1500h,抽样误差为100h,此数据只能说明这同期生产的10000个灯泡的平均使用寿命的可能范围,而不是一个具体的数值。即全部灯泡的平均使用寿命为
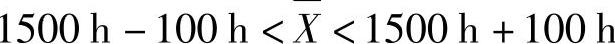
即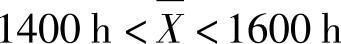
将其转换为一般的推断公式为
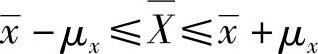
而利用成数抽样误差的一般推断公式为
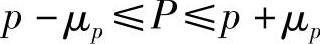
统计理论证明,抽样误差范围与把握程度之间有着可用数学公式表示的密切联系。由典型的概率分布曲线可知:扩大抽样误差的范围,就能够提高抽样判断的把握程度。统计数学证明:当抽样误差范围为1μ时,则对应的把握程度为0.6827,即把握概率为68.27%;当抽样误差范围为1.5μ时,则对应的把握程度为0.8664;当抽样误差范围为2μ时,则对应的把握程度为0.9545;当抽样误差范围为3μ时,则对应的把握程度为0.9973。由此可知,把握程度随抽样误差范围的扩大而提高;或者说,当测量手段、精度等一定时,把握程度的提高必须以抽样误差范围的扩大为代价。
上例中的抽样误差范围扩大或缩小的倍数又称为概率度,以符号t表示。概率度与概率之间的对应关系可由一个积分表达式F(t)列出,但由于积分式的计算繁琐,实际工作中,常将其列成“正态分布概率表”,先计算出t的值,再查表按t与F(t)的对应关系查出F(t)的具体数值。常见的t与F(t)的对应表见表3-1。
表3-1 常见正态分布概率表

极限抽样误差是测量工作中规定的测量误差范围,常表示为t倍的抽样误差的形式。它们之间的数量关系如下
Δ=tμ
式中Δ——极限抽样误差;
t——概率度;(https://www.xing528.com)
μ——抽样误差。
此公式也可用如下的文字表达形式表述:
极限抽样误差=概率度×抽样误差
极限抽样误差的具体计算公式常见的有如下几种形式。
(1)平均数的极限抽样误差的计算
1)重复抽样。

2)不重复抽样。
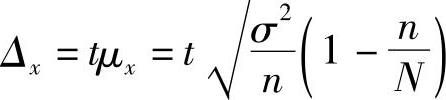
(2)成数的极限抽样误差的计算
1)重复抽样。
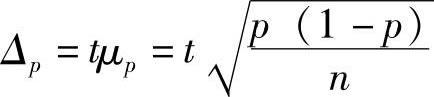
2)不重复抽样。
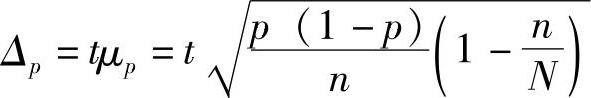
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




