如何利用改正数计算均方误差

式（2-2）为用真误差求一组测量值中误差的公式，即

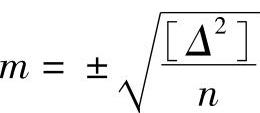
但测量值的真误差只有在真值为已知时才能确定，而未知量的真值往往是不知道的，因此无法用其来衡量测量值的精度。为此，在实际的工作中，常用的方法是用算术平均值与测量值之差来计算出均方误差的。算术平均值与测量值之差称为测量值的改正数，或者称最或然误差。以下是用改正数表示均方误差的计算公式的推导过程。

设l₁、l₂、…、l_n为一组等精度的测量值，x为测量值的算术平均值，以v表示改正数，则有

将上式两端相加得

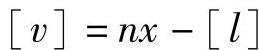
而将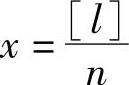代入上式，可得

由上式可知，对于任一未知量的一组等精度测量值，改正数的代数和应等于零。这一结论可作为算术平均值和改正数的计算工作的校核。

通过研究改正数v_i与真误差Δ_i之间的关系，可以推导出以改正数表示的测量值均方误差计算公式。

根据真误差的定义式（2-4），由式（2-4）与式（2-5）对应相减，得

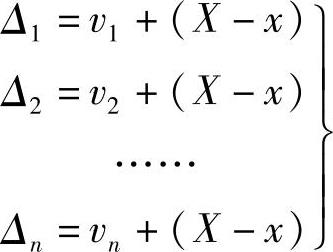
将上式两边平方，并相加得

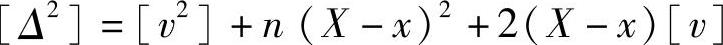
因[v]=0，所以

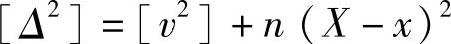
上式两边除以n，得

因为（X-x）是算术平均值的真误差，以δ表示，则(https://www.xing528.com)

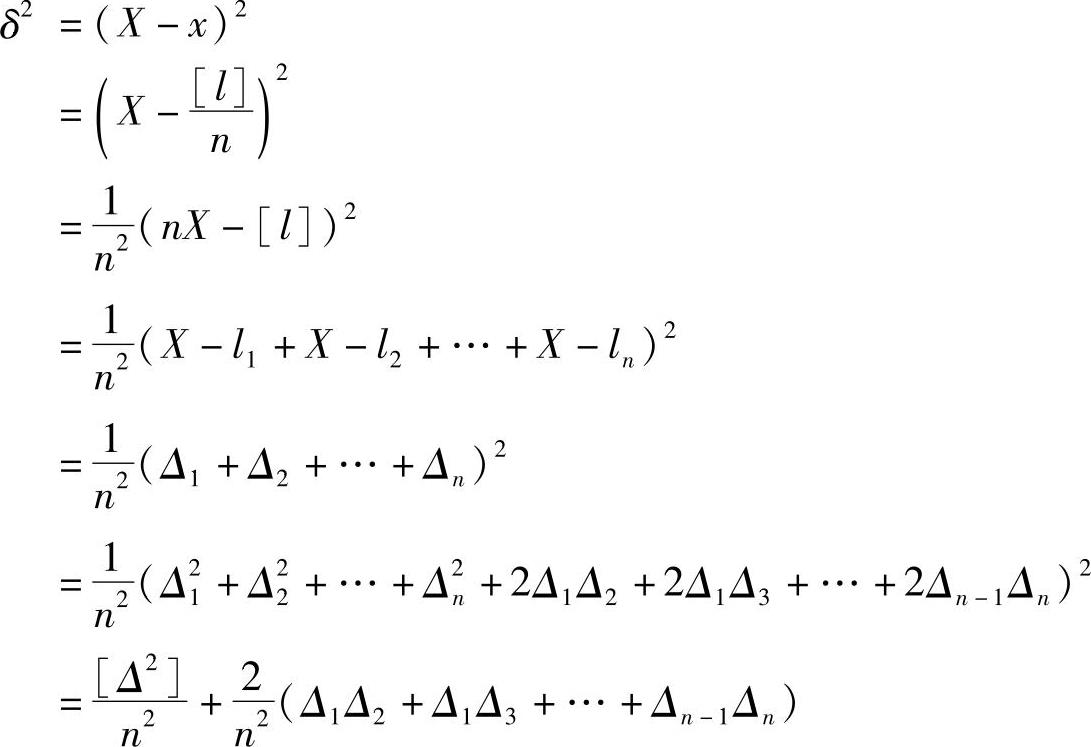
由于Δ₁、Δ₂、…、Δ_n是随机误差，故Δ₁Δ₂、Δ₁Δ₃、…、Δ_n-1Δ_n也具有随机误差的性质。根据随机误差第四个特性，当n相当大时，其总和应接近于零；当n为较大的有效值时，其值也远比[Δ²]小，可以忽略不计。这样，式（2-7）可以近似地写成

按照中误差的定义式（2-2），又有

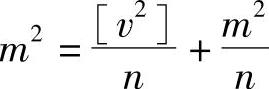
即

式（2-9）即为利用观测值的改正数计算均方误差的公式。3.算术平均值的均方误差

根据误差理论，算术平均值的均方误差为

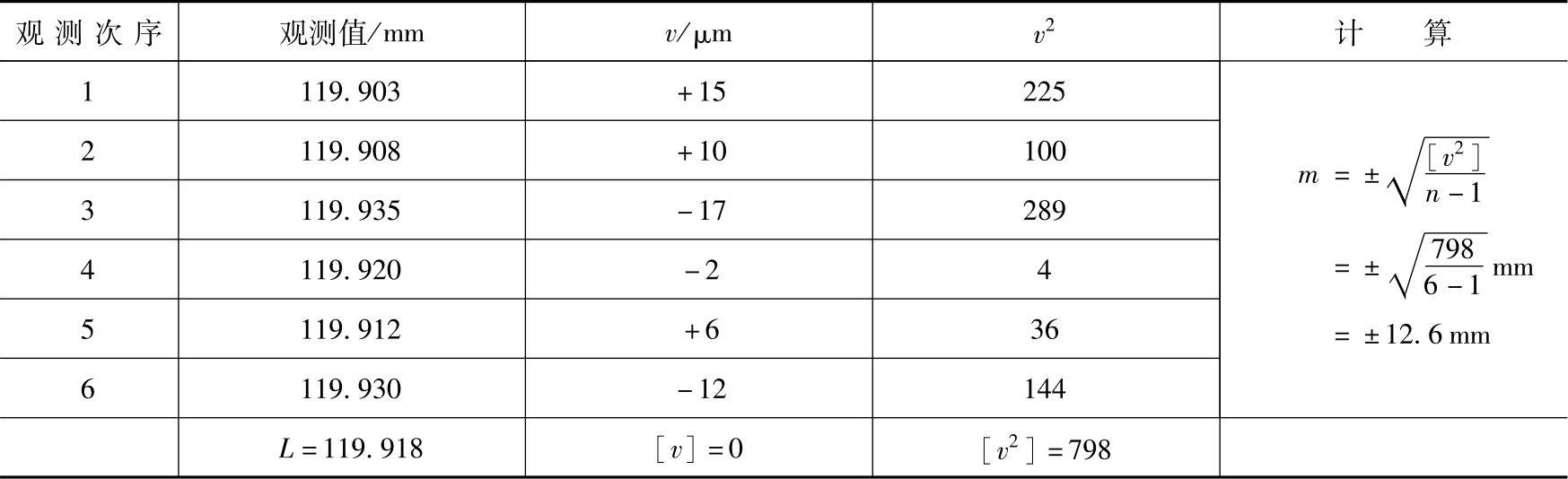
例如，对某零件的直径进行了六次等精度观测，其各次观测值见表2-3。试求该零件直径的算术平均值、观测值的均方误差及算术平均值中误差。

算术平均值的中误差为

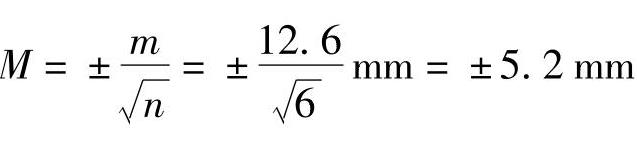
表2-3 算术平均值的均方误差计算表

课后任务：

1）根据学习内容，查找相关的图书资料及网上资料，加深对此任务内容的理解。

2）根据对多组测量数据的分析计算，熟练掌握误差分析的基本方法。