随机误差的规律性及特性分析

由前述可知，从表面上看随机误差是没有规律的，但对相同观测条件下的大量误差的总体来说，它具有一定的规律性，并且随着观测次数的增多，这种规律性越明显。下面的实例说明了在角度观察中随机误差的规律性，这种规律在长度测量中也是同样存在的。

例如，在相同的测量条件下，测量了162个三角形的全部内角。由于随机误差存在于观测值中，三角形三内角测量值之和l不等于真值X（显然，三角形的内角和的真值为180°），真值与测量值之差称为真误差Δ，则

Δ_i=X-l_i（i=1、2、…、162） （2-1）

根据式（2-1），可计算出的162个三角形三内角之和的真误差，以误差区间为0.2″，根据其误差的正、负和大小，可列出表2-1。

表 2-1

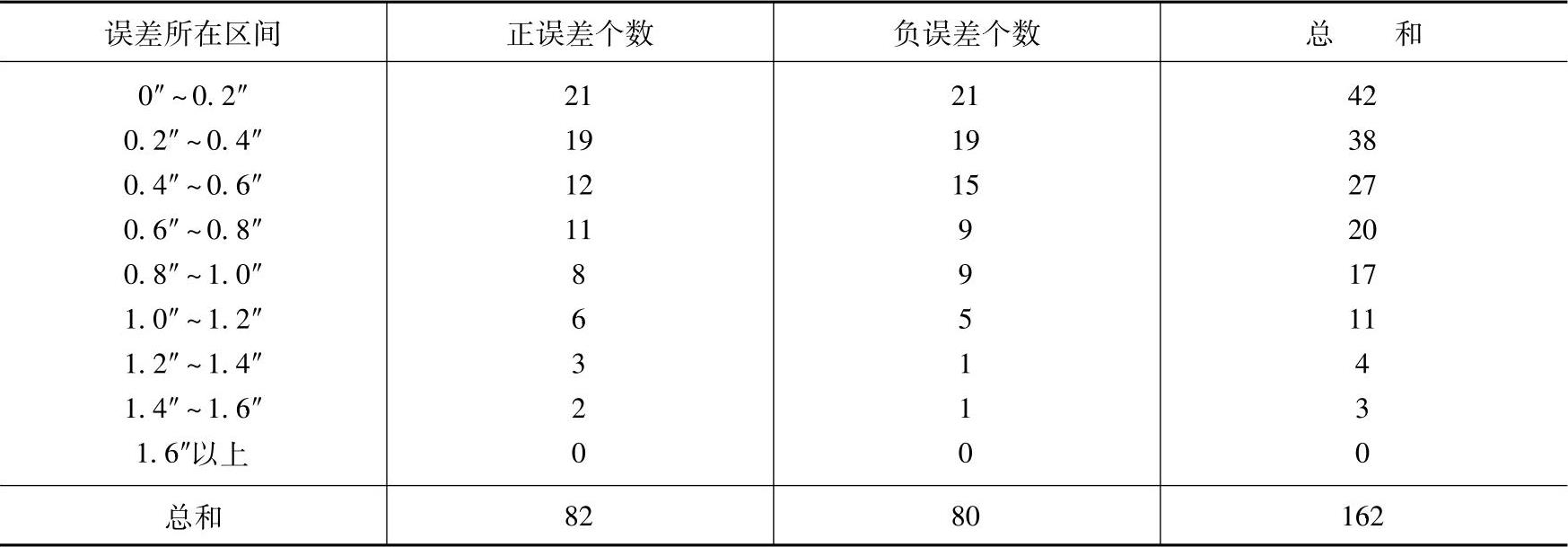
由表2-1中数据可以看出该组误差的分布规律如下：①小误差的个数比大误差多；②绝对值相等的正、负误差的个数大致相等；③最大的误差不超过一定值（1.6″以上）。

通过对反复的实践、研究，在统计了大量的各种观测列结果后，总结出的随机误差列具有如下特性：

1）在一定的观测条件下，随机误差的绝对值不会超过一定的数值。(www.xing528.com)

2）绝对值小的误差比绝对值大的误差出现的机会多。

3）绝对值相等的正误差和负误差出现的机会相等。

4）随机误差的算术平均值随着观测次数的无限增加而趋于零，即

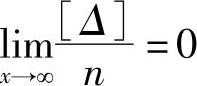
式中n——测量次数。

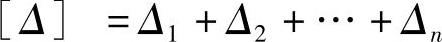
由随机误差的特性可知，当对某量有足够多的测量次数时，其正误差和负误差可以相互抵消。因此，我们可以采用多次测量，取测量结果的算术平均值作为最终结果。