霍尔测试技术介绍及优化方法

在Ⅲ族氮化物半导体电学性质的研究中,霍尔(Hall)测量是表征其载流子浓度和载流子输运性质的重要手段。

1.霍尔效应的基本原理

霍尔效应是霍尔(Hall)在研究关于载流导体在磁场中的受力性质时发现的一种现象。当电流垂直于外磁场通过导体时,载流子会发生偏转,使得在垂直于电流和磁场的方向会产生电势差,这一现象就是霍尔效应,所产生的电势差称为霍尔电压。

如图2.6.1所示,以电子为例,在磁场作用下,运动的电子受到洛伦兹力作用,根据左手定则,在如图2.6.1所示的特定磁场B和电流I作用下,电子向左边聚集,形成横向电场。横向电场也会对电子产生电场力的作用。随着电子聚集数量的增多,电场随之增大,直到电场力和洛伦兹力达到平衡,电子不再聚集,形成稳定的霍尔电压U H。

图2.6.1　霍尔效应原理图

假设样品中电子的浓度均匀为n,电荷量为q,运动速度为v,样品的厚度为d,宽度为b,根据力平衡条件,可得

又因为

联立以上两式得

令

则

式中,R H被称为霍尔系数。

以上推得霍尔系数是针对导电粒子是电子的情况,霍尔系数是负值;若导电粒子是空穴,假设空穴浓度为p,则霍尔系数的表达式为R H=是正值。因此,可以通过霍尔系数的正负来判定材料的导电类型。若已知被测样品的厚度为d,还可以通过测量霍尔系数来得到样品的载流子浓度。

另一方面,还是以n型掺杂的半导体为例,根据半导体物理的知识,样品的电阻率ρ可以表示为

式中,μ为电子的霍尔迁移率。考虑载流子的速度分布会影响到电导迁移率,这里的迁移率是霍尔迁移率,并不一定等于载流子的实际电导迁移率。

联立式(2.6.4)和式(2.6.6),可得

因此,理论上只要测得材料的霍尔系数R H和电阻率ρ,就能得到材料的载流子浓度和迁移率信息。

2.霍尔的测量方法——范德堡法

范德堡法是一种常用于测量样品的电阻率和霍尔系数的方法。它的功能是能够精确测量任意形状样品的性质,但需要在材料表面制作四个对称的欧姆接触电极,如图2.6.2所示。

图2.6.2　范德堡法测试示意图

这种方法对样品形状没有特殊要求,但要求其厚度和电阻率均匀,并要求表面没有孔洞。四个接触点要尽可能小,并且这四个接触点必须位于薄膜的边缘。在实际测量中,为了简化测量和计算,常常把待测薄膜设计为正方形,将四个接触点置于正方形的四个顶点处,使这四个接触点在几何上是完全等效的。

(1)霍尔系数R H的测量。

在理想情况下,对于已知薄膜样品的厚度,如果在垂直于样品表面方向施加特定的磁场,在1,3触点之间通入恒定电流,要测量4,2触点之间的霍尔电压,根据式(2.6.5)就能得到霍尔系数。但是,在进行霍尔测量的过程中,除了霍尔效应,可能还存在一些影响测量结果的副效应,这主要包括爱廷豪森效应、能斯脱效应、里纪-勒杜克效应和不等位效应[25]。

①爱廷豪森效应:如图2.6.3所示,当对样品通以x方向的电流和z方向的磁场,由于电子(N型半导体)或空穴(P型半导体)的速度并不是完全相等的,所以速度快和慢的电子(或空穴)的偏转半径不同,在y轴方向产生的温度梯度也不同,由此温度梯度引起的y方向的温差电动势就称为爱廷豪森电压,用符号U E表示。研究表明,U E的大小和方向与电流I和磁场B的大小和方向有关,且跟霍尔电压U H与电流和磁场的相关趋势相同,因此这一效应在用范德堡法进行霍尔测试中难以消除。

图2.6.3　爱廷豪森效应示意图

②能斯脱效应:对样品沿x方向通以电流,两端电极与样品的接触电阻如果存在差异,焦耳热会导致x方向产生温度梯度,进而引起电子(空穴)的扩散。在z方向磁场的作用下,载流子扩散流发生偏转,在y方向产生的电位差称为能斯脱电压,用U N表示。U N的符号只与磁场方向有关,可通过改变磁场方向消除。

③里纪-勒杜克效应:x方向温差引起的热扩散流在z方向磁场作用下偏转,电子(空穴)速度的分布在y方向产生温度梯度,此温度梯度引起的温差电动势称为里纪-勒杜克电压,用U RL表示。U RL的方向与U N类似,也只与磁场方向相关,可通过改变磁场方向来消除。

④不等位效应:没有加磁场的情况下,若只在样品的x方向通以电流,在x方向必然存在电势差。在制备霍尔样品时,y方向的测量电极难以精准地处在理想的等位面上,如图2.6.4所示。假设两个测量电极分别在A和B位置,由于两者不在同一等位面,所以电极间存在电势差,这个电势差就是不等位效应引起的电势差,用U 0表示。显然,U 0只与I的方向有关,可以通过改变电流方向来消除。

(www.xing528.com)

图2.6.4　不等位效应示意图

由于以上所述副效应的存在,在图2.6.2所示中,若在1,3触点之间通入恒定电流,4,2触点之间测量的电压值并不等于真实的霍尔电压,而是包含了各种副效应引起的附加电压,所以必须设法减轻副效应的影响。从对每种副效应的讨论中可以看到,附加电压的方向可能跟磁场或电流的方向有关。因此,可在各种电流I和磁场B的方向组合下来测量4,2之间的电压值,再经过数据处理,就可消除副效应的影响。设电流从1流到3的方向为正,磁场向上为正,设(+B,+I),(+B,-I),(-B,-I),(-B,+I)四种组合下4,2触点之间的电压分别是U 1,U 2,U 3,U 4,即

4,2两点间的霍尔电压用U H(4,2)表示,则

那么

从式(2.6.12)可以看到,通过改变磁场和电流的方向,可以有效地消除能斯脱效应、里纪-勒杜克效应和不等位效应对霍尔电压测试的影响,而爱廷豪森效应的影响不能消除,但这个效应引起的误差不大,可以忽略不计。

以上是1,3触点间通电流,测量4,2触点间电压的情况,也可以用相同的方法给2,4触点间通电流,测量1,3触点间的霍尔电压U H(1,3)。在理论上这两种情况下测得的霍尔电压应该相等,可以用这两个霍尔电压的均值来表示样品在特定大小的电流和磁场下的霍尔电压U H,从而进一步减小测量误差,则U H可以表示为

将此霍尔电压带入式(2.6.5),已知样品的厚度为d,即能得到霍尔系数,从而进一步能够推算出样品的导电类型和载流子的浓度。

(2)电阻率ρ的测量。在电阻率的测量中,在图2.6.2所示中,在一对相邻的电极通入电流,测量另一对电极之间的电位差,即可得到电阻。利用在电极1、2和2、3之间通入电流I 12和I 23,分别测量4、3和1、4电极之间的电压U 43和U 14,则两次测量得到的电阻分别为

根据范德堡理论,电阻率可表示为

式中,f为范德堡修正因子,这取决于R 12,43和R 23,14的比值,反映样品几何形状以及电极配置的不对称性。

也可以在电极3、4和4、1之间通入电流I 34和I 41,分别测量2、1和3、2之间的电压U 21和U 32,得到电阻R 34,21和R 41,32和由此算得的电阻率分别为

为了减小测量误差带来的影响,电阻率ρ通常取的平均值,即

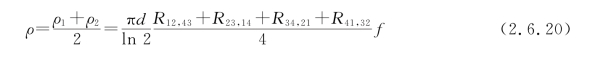
至此,通过范德堡测试方法分别得到了霍尔系数和电阻率,再根据式(2.6.7),即能推算出样品的迁移率。

(3)在未知样品厚度时,方块电阻、面电荷密度和迁移率的测量。通过以上讨论可知,霍尔系数和电阻率的数值都要在已知样品厚度d的情况下才能获得,从而得到相应的载流子浓度和迁移率。如果测量厚度不明确的样品或者对于二维材料,用范德堡测试方法也可以测得面电荷密度和迁移率。

根据体载流子浓度n和霍尔测试样品的厚度d,可以计算出面电荷密度为

联立式(2.6.3),可得

霍尔电压与前述测试方法相同,从式(2.6.22)可见,面电荷密度与样品厚度无关,即使样品厚度未知,也可以通过霍尔测试得到其面电荷密度。

方块电阻是指一个正方形的薄膜导电材料边到边之间的电阻,通常用R sheet表示,它与样品的尺寸无关,只与薄膜材料的厚度有关,方块电阻的单位是Ω/□,方块电阻与电阻率的关系是联立式(2.6.20)得

由式(2.6.24)可知,方块电阻与厚度无关。因此,在未知样品厚度的情况下,也可以直接测得样品的方块电阻。

又联立式(2.6.6)、式(2.6.21)和式(2.6.23)可得

显然,在测得面电荷密度和方块电阻以后,就可以推算出样品的载流子迁移率。

3.霍尔测试系统

霍尔测试系统主要由电流源、电压表、开关系统、电磁系统、控温系统和皮安表等部件组成,如图2.6.5所示。其中,电流源提供源电流;电压表和皮安表分别用来测量电压和电流;电磁系统的主要作用是负责磁场的产生和测量,一般由电磁铁、电磁铁激励电源、电磁铁电源控制系统和磁场场强计组成;由于样品载流子浓度、迁移率等物理量都会随着温度的变化而变化,因此精确的霍尔测量都要在给定的温度条件下进行。控温系统主要用来进行温度的控制和测量,主要包含恒温器、控温/测温仪、机械泵、真空泵和真空检测仪等部件。

图2.6.5　霍尔测试系统示意图