共轭梯度迭代法在管道漏磁内检测缺陷量化中的优势应用

1.共轭梯度迭代法基本原理

在20世纪50年代初期，为了求解具有正定系数矩阵的线性方程组，计算数学家Hestenes和几何学家Stiefel首次提出了一个新的求解线性方程组的迭代方法——共轭梯度（Conjugate Gradient）法。共轭梯度法又称为共轭斜量法。而后，科学家Fletcher和Reeves将此方法进一步推广到非线性优化领域中，得到了求解一般函数极小值问题的共轭梯度法（也称FR法）。

共轭梯度迭代法的基本迭代思想是：寻找一组两两共轭的线性无关的矢量，以这组向量作为迭代法的迭代方向，设置在定义域内的任意矢量为初始矢量，依次迭代，每次迭代后，根据每步得到的计算结果不断地改变迭代方向和迭代步长，经过有限次迭代后便可得到最优解。

针对求解无约束优化问题：min{f（x），x∈Rⁿ}，一般采用共轭梯度迭代法来寻求f（x）在定义域内的最小值。其中，f（x）是Rⁿ→R的连续可微函数。特别是将其运用在求解大规模优化计算问题时，该算法的收敛迅速和存储量小的优点就展现出来了，因此得到广泛的应用。

每一种迭代方法都有其固定的迭代格式，共轭梯度迭代法的主要迭代格式为

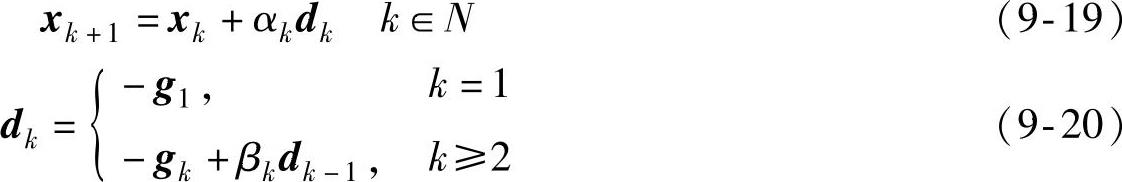
式中，d_k为f（x）在x_k点的搜索方向；α_k为该搜索方向上的搜索步长；g_k=▽f（x_k）；β_k为一个标量参数，当β_k取不同的公式时就会得到不同的共轭梯度法，常见的β_k形式有β_k^PRP，βk^CD，βk^HS，βK^FR等，计算公式分别为

式中，‖‖为取欧几里得范数。

当计算得到β_k和g_k后，就可以确定出搜索方向d_k。在确定搜索方向上的搜索步长α_k时，还需要用到以下几种搜索方法。

（1）精确线搜索 搜寻α_k＞0，且满足条件：

从理论分析的角度来说，运用精确的线搜索，可以得到使目标函数得到最大下降值的搜索步长。由于该方法具有步长搜索精确和搜索计算速度快等特点，因此成为线搜索方法中最理想的一种方法。但是，从运算效率的角度来说，该方法具有计算复杂、计算量大的缺点，采用精确线搜索方法来确定搜索步长要付出较高的代价。因此，精确线搜索方法从运算效率的角度出发不能说是一种理想的方法。在实际确定搜索步长的运算中，通常采取折中的方法，既可以减少计算量，又可以达到确定搜索步长的目的。

在共轭梯度迭代法中，通常采用下面两种非精确线搜索的方法来确定搜索方向上的搜索步长。

（2）Wolfe线搜索 搜寻α_k＞0，且满足条件：

式中，g_k=▽f（x_k）；δ和σ为常数项，且满足δ∈（0，1/2），σ∈（δ，1）。

式（9-27）的作用为使得目标函数值的下降量至少与其切线方向的下降量成正比。式（9-27）的作用为在确保目标函数的函数值拥有充分的下降量的同时，防止搜索步长过小。

（3）强Wolfe线搜索 搜寻α_k＞0，且满足式（9-27）和

|d_kg（x_k+α_kd_k）|≤σ|d^T_kg_k| （9-28）

式中，δ和σ为常数项，且满足δ∈（0，1/2），σ∈（δ，1）。

当σ=0时，式（9-28）的右边项为零，则一定有g（x_k+α_kd_k）^Td_k=0。因此当σ的值趋近于零时，强Wolfe线搜索的计算结果就趋近于精确线搜索的计算结果。

对于一般的非线性函数，FR共轭梯度迭代方法具有良好的全局收敛性，因此一直都受到研究人员的关注，应用于不同的领域。

2.缺陷量化模型的建立

建立电磁场反问题的数学模型为f_j（x₁，x₂，…，x_n），其中j=1，2，…，n，该模型是n元二次连续可微函数，这n个函数均定义在n维空间区域D上，并且这n个函数的值域也包含在n维空间区域D内。建立非线性方程组f_j（x₁，x₂，…，x_n）=0，通过求解该方程组，得到电磁场反问题的计算结果。

管道漏磁内检测缺陷量化问题是建立在二维空间上的，因此选取相应电磁场反问题的数学模型中的n=2，则建立的缺陷量化模型是由f₁和f₂组成的方程组。

根据解决电磁场正问题的管道漏磁内检测二维有限元仿真分析和二元函数最小二乘法曲线拟合方法，已经得到了管道漏磁内检测二维实体模型有限元分析的缺陷处漏磁信号径向分量B_x特征量（峰峰值和峰峰间距）的非线性拟合方程组。在电磁场正问题的基础上，构建出管道漏磁内检测信号重构问题的数学模型，即缺陷处漏磁信号径向分量B_x特征量的非线性方程组，即

式中，d为待重构的缺陷深度；l为待重构的缺陷长度；p为检测到的漏磁信号径向分量B_x的峰峰值；q为检测到的漏磁信号径向分量B_x的峰峰间距。

在管道漏磁内检测缺陷量化分析问题中，p、q为已知检测到的信号数据，而d、l为所要反演的缺陷几何参数，即要求解的未知数值。

3.共轭梯度迭代算法的实现

（1）非线性方程组求解的基本理论 采用FR共轭梯度迭代算法求解管道漏磁内检测缺陷量化分析问题的非线性方程组（9-30）。该算法具有不需要选取任何迭代参数和收敛速度快的特点，只要计算出搜索方向和该方向上的搜索步长，每迭代一次，都要重新计算一次搜索方向和搜索步长，并且依次沿着求解出的n个非零的共轭搜索方向进行搜索，就可以得到比较理想的数值解，即可以得到较准确的重构结果。(www.xing528.com)

求解非线性方程组要用到函数f₁、f₂对未知数d、l的雅可比（Jacobian）矩阵，即

由于在求解矩阵J时先要求出它的4个元素，计算量较大，因此为了减少每一次迭代的计算量，通常以求解差商的方法来代替求解矩阵J中方程的偏导数，如式（9-31）和式（9-32）所示。

式中，j为方程组中方程的标号，本文中取j=1，2；h为与j无关的常数。

（2）算法程序流程 共轭梯度迭代算法的程序流程如图9-5所示。

图9-5 程序流程

（3）算法实现步骤

①给定初始点（d₀，l₀）及精度eps＞0。

②计算J₀（d₀，l₀），令P₀=-J₀（d₀，l₀），k=0。

③求搜索步长λ_k，计算（d_k+1，l_k+1）=（d_k，l_k）+P_kλ_k，J_k（d_k，l_k）。

④若‖（d_k+1，l_k+1）-（d_k，l_k）‖＜eps，迭代结束，否则转⑤。

⑤计算。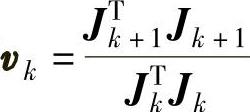

⑥确定P_k为搜索方向。若|v_k|＜1，则P_k+1=-J_k+1+P_k×v_k；否则P_k+1=-J_k+1，令k=k+1，转回③。

4.缺陷量化仿真实验与结果分析

管道的壁厚为10mm；电磁场正问题为ANSYS有限元分析软件对管道漏磁内检测二维仿真，建立半椭圆形缺陷模型，并且将缺陷模型建立在管壁外侧；缺陷的几何参数为缺陷的长度和深度；在电磁场反问题中，通过ANSYS有限元分析软件的路径操作功能，采样得到缺陷处漏磁信号径向分量B_x数据，利用MATLAB编写的程序提取出漏磁信号径向分量B_x特征值，即漏磁信号径向分量B_x峰峰值和漏磁信号径向分量B_x峰峰间距；将提取出的特征值作为已知，输入到编写好的迭代算法中，便可求解出缺陷几何参数的最优解。

（1）管道漏磁内检测二维缺陷量化仿真实验的流程如图9-6所示。

（2）管道漏磁内检测二维缺陷量化仿真实验的步骤

①随机设置缺陷的几何参数（缺陷的深度和长度），即待求缺陷量化结果。

②利用ANSYS有限元分析软件建立管道漏磁内检测实体模型，并进行电磁场二维仿真计算。

③利用ANSYS有限元分析软件的路径操作功能，设定一条路径（路径长80mm、提离值取1mm），通过采样得到该路径上采样点的漏磁信号径向分量B_x。

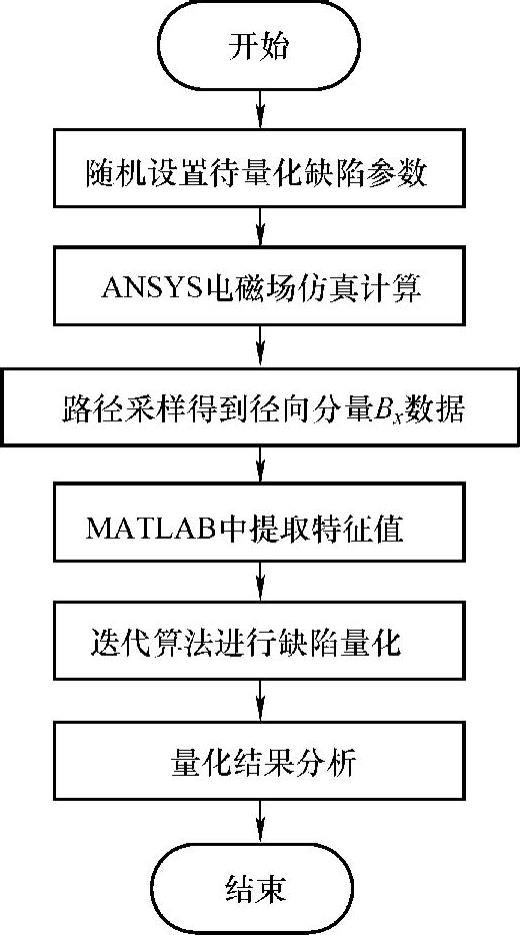
图9-6 量化仿真实验流程

④将ANSYS有限元分析软件生成的缺陷处漏磁信号径向分量B_x数据导入MATLAB软件，从中提取漏磁信号径向分量B_x的特征值。

⑤将第④步中得到的特征值作为已知，代入共轭梯度迭代算法中，得到相对应的缺陷量化结果。

5.管道漏磁内检测缺陷量化仿真实验结果分析

按照管道漏磁内检测缺陷量化仿真实验的步骤完成仿真实验，并且选取3组缺陷量化的仿真实验结果，见表9-3。

表9-3 缺陷量化仿真实验结果

从表中缺陷量化仿真实验结果的数据可以明显看出：三组共轭梯度迭代算法的缺陷量化的结果误差均在10%以内，准确地反演出了缺陷的几何参数，效果较好。