漏磁内检测的正反问题分析与解决

缺陷的定量检测主要是要分析、求解缺陷漏磁场的正问题（从给定的激励源和已知参数的缺陷来计算所对应的漏磁场），以及其反问题（从给定的缺陷漏磁场来估计对应的缺陷参数和轮廓）。漏磁内检测信号的量化过程，即根据漏磁内检测信号确定出对应缺陷的长、宽、深等参数的过程，称为对漏磁内检测信号的反问题。

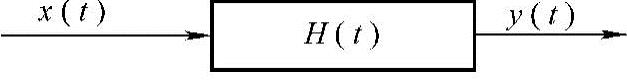
图9-1 系统结构模型

在分析信号与系统的关系时，使用图9-1所示的模型，x（t）作为输入的激励信号，y（t）作为输出的响应信号，H（t）作为系统函数。考虑到信号与系统之间的关系和漏磁检测的过程相似，提出一种解释漏磁检测问题的系统模型。一个普通的漏磁检测系统可以用图9-1所示的线性模型表示，它包括激励源x（t）、探头测量值y（t）以及漏磁场和缺陷相互作用的变换函数H（t）。

在漏磁检测系统中，x（t）为激励源以及缺陷的参数，缺陷参数可以简单地等同为长度、宽度、深度或完整的三维（3D）轮廓，作为系统的输入；y（t）可等效为包含缺陷参数信息的漏磁检测信号，作为系统的输出；H（t）就是对应地将x（t）映射到y（t）的函数。

通过图9-1所示的模型可以这样分析漏磁内检测系统的正问题和反问题：在已知输入x（t）和系统H（t）的情况下，确定输出y（t），这就是漏磁检测的正问题；已知输入x（t）和输出y（t），确定H（t）的系统识别问题和已知系统H（t）和输出y（t），确定输入x（t）的反卷积问题的情况，都可以归为漏磁检测的反问题。漏磁检测中，正问题包括使用输入激励，估计缺陷产生的检测信号；而反问题包括使用包含在检测信号中的信息，估计缺陷参数（即缺陷的等价长度、宽度和深度）或缺陷轮廓。这样的反问题也可以归结为麦克斯韦方程的反问题，即已知空间（或局部）电磁场分布，求激励源或媒质分布。

电磁场的反问题从应用的角度可以分为两类：优化设计问题和参数识辨问题。其中优化设计问题又称为综合问题。这两类反问题的求解对象可以完全一样，不同的是，优化设计问题一般不要求求解的唯一性但要求解的存在性，而参数识辨问题却需要给出和客观实际吻合的唯一解。优化设计问题按求解对象的不同大致可分为源综合、边界条件综合、材料性质综合和形状综合问题；参数识辨问题则可分为位置识辨、形状识辨和媒质参数识辨等。漏磁内检测缺陷量化问题就属于其中的形状识辨问题。

电磁场的正问题通常是良态的，解决正问题的方法有解析法和数值计算法，在很长一段时间被广泛应用。但反问题一般是病态的，既缺乏唯一性，又缺乏检测信号对缺陷的连续性。从电磁场中反问题的数学模型来看，优化设计问题的数学模型通常表现为无约束或有约束的多目标优化问题，本质上就是一个极值问题；而参数识辨问题则表现为线性或非线性算子方程，有时可以直接求解该方程，但更多的时候是利用最小二乘原理将其转化为极小值问题（优化问题），由此引来的一个问题是“第二极值点”的出现。(www.xing528.com)

一个优化问题通常表述为

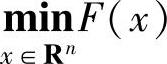
式中，x为待优化的参数组；F≥0为目标函数。

要找出使F取值最小的x（最优解）。一般情况下，很难直接求解该问题，而是转而通过迭代过程，即多次计算不同x所对应的目标函数值，来逐步逼近最优解。优化问题的求解方法分为两类：确定性方法和随机性方法。

确定性方法是指在迭代过程中根据每步迭代所确定的搜索方向与步长而一步一步地进行搜索，当前步迭代解所对应的目标函数值一定比前一次迭代解对应的目标函数值小。不同的确定性方法主要是指搜索方向不同，如最速下降法、拟牛顿法、共轭梯度法等。确定性方法是靠当前搜索位置的邻域的特点来确定下一步的搜索位置（同时也实现了非线性问题的局部线性化），所以本质上是一种局部寻优，它们寻找局部最优解的效率很高，但在多极值问题中几乎不具备寻找全局最优解的能力。

随机性方法又称为蒙特卡罗（Monte Carlo）法，是指每步迭代中都有（伪）随机数参与了当前迭代解的生成，或者说搜索方向和步长具有随机性。蒙特卡罗法又分为传统蒙特卡罗法和现代蒙特卡罗法。传统蒙特卡罗法进行完全随机的“盲目”搜索，即认为所有可能解都等概率出现，其列举量较穷举法小，但代价是无法保证找到最优解，只能找出满足给定条件的部分解集。现代蒙特卡罗法则是有指导性地进行随机搜索，它使不同的可能解具有不同的出现概率，是启发式的，是对传统蒙特卡罗法的发展。现代蒙特卡罗法的典型代表是遗传算法、人工神经元网络法、模拟退火法等。对比确定性方法，蒙特卡罗法的优点在于：普遍性强，不需要区分待求问题是线性的还是非线性的，是病态的还是良态的；可以处理正算子非常复杂或无法用解析式表示的问题；具有较强的全局寻优能力。其缺点是计算量通常较大，且随问题阶数剧烈增长。