管道漏磁检测数据的无损压缩方法

1.检测无损压缩

传统的无损编码方法，如霍夫曼编码、算术编码等熵编码以及无损预测编码可以实现完全无损的压缩，但压缩比很低（一般在3∶1左右）；有损预测编码及变换编码具有较大的压缩比。检测无损压缩是一种能够保留所有检测重要信息的有损数据压缩方法。它通过对重要的检测相关数据采用无损压缩而对不能提供检测相关信息的非重要数据进行大压缩比的有损压缩，从而在保证检测精度的同时获得较好的总体压缩效果。在很多检测应用中，只有某些特殊幅值、频率、纹理或形状所对应的数据才是与检测相关的，而其他部分的数据则只具有很小的检测重要性。检测无损压缩的关键就是要根据检测的原理和要求识别出感兴趣区域（Regions of Interest，RoI），从而实现对不同重要程度的数据采用不同的压缩方法。例如，在一维的超声检测数据中，我们通常只对超过某一阈值的数据感兴趣，因此可以采用较小的比特数表示小于阈值的数据或者只记录这些数据的数目，而对超过阈值的数据则使用较多的比特数表示。对于图像或视频检测数据的检测无损压缩，则要使用图像分割算法从原数据中分离出感兴趣区域和感兴趣帧。

在管道漏磁检测数据中，与管道缺陷和管道特征物对应的数据是检测结果分析时的重要数据，而管道“健康”区域所对应的数据在数据处理时则是不重要的。由于缺陷和特征物在管道中仅占较小的部分，而且这部分数据具有较大的动态范围和较大的变化率等特性，因此可以从全部数据中分离出这些数据并对它们采用无损压缩方法或失真度较小的有损压缩方法压缩，而对其余数据采用大压缩比的有损压缩方法，从而在保证管道评价质量的基础上获得满意的压缩效果。

2.检测重要区域的分割

（1）一阶差分处理 一阶差分处理是在许多压缩方法中都得到应用的无损预处理方法。通过计算差分，可以提高数据的可压缩性。由于每个探头检测到的相邻数据间有较强的相关性，相邻数据间的差值就会比较小，而且差值数据的分布范围要比原始数据更加集中。原始数据如图8-16所示，对各通道数据进行一阶差分处理后数据的灰度图如图8-17所示（差分后的数据都加上了128，以符合灰度图像数据的范围），原始数据及差分数据的灰度直方图分别如图8-18和图8-19所示。可以看出，经过差分处理后，图像的灰度范围缩小了，数据可压缩性得到了增强。

图8-16 原始的漏磁检测数据

图8-17 经过一阶差分处理后数据的灰度图

图8-18 原数据的灰度直方图

图8-19 差分处理后的灰度直方图

如前所述，在缺陷处以及管道特征物处的漏磁信号都具有较大的变化率。一阶差分值也就是信号的变化率，因此差分计算的结果还可以用来分割检测重要区域。

一阶差分实际上就是DPCM编码中最简单的前值预测法。由于实际上并不是所有的数据都需要无损压缩，因此可以对非重要区域的差分数据采用一定的量化策略进行有损压缩，从而获得更大的压缩比。

差分处理也带来了一个问题，即误码扩散。如果差分处理后的数据在编码时产生误码，则此后所有的数据在恢复时就都会产生错误。

（2）重要区域分割的差分阈值方法 为了实现数据的检测无损压缩，需要从漏磁图像中分割出重要区域，并对这些区域使用无损压缩方法。首先把漏磁数据分成较小的数据块，再在数据块内计算各通道数据的差分，并判断差分值是否大于某一阈值，如果是就认为这个数据块是重要的。这种方法的一个关键点是确定数据块的大小。如果数据块太大，由于重要数据的分布具有不规则性，会导致太多的重要块而影响压缩效率；如果数据块太小，当采用霍夫曼编码时，由于编码器必须保存一些块初值，会导致压缩比较低；而采用提升小波变换和SPIHT编码（见后文介绍）时，也会影响压缩效果。具体分块的大小，要依据采样间隔等条件通过试验的方法确定。对检测出的重要数据块加以标识后，后续的压缩步骤就可以根据标识选择对此区域的压缩方法。

通过数据分块不仅可以保证发生误码时误码被限制在块范围内，而且还可以降低后续处理过程中存储量要求。在利用硬件实现时，就可以仅使用FPGA内部的RAM，而不必扩展外部RAM，从而提高运算速度并减小块面积。选取一段原始检测曲线，如图8-20所示。对图8-20中数据采用10×10分块、差分阈值为3时得到的重要数据块分布，得出的检测重要区域如图8-21所示。图中亮色区域是分割出的重要区域，它很好地覆盖了缺陷部分。

图8-20 原始检测曲线

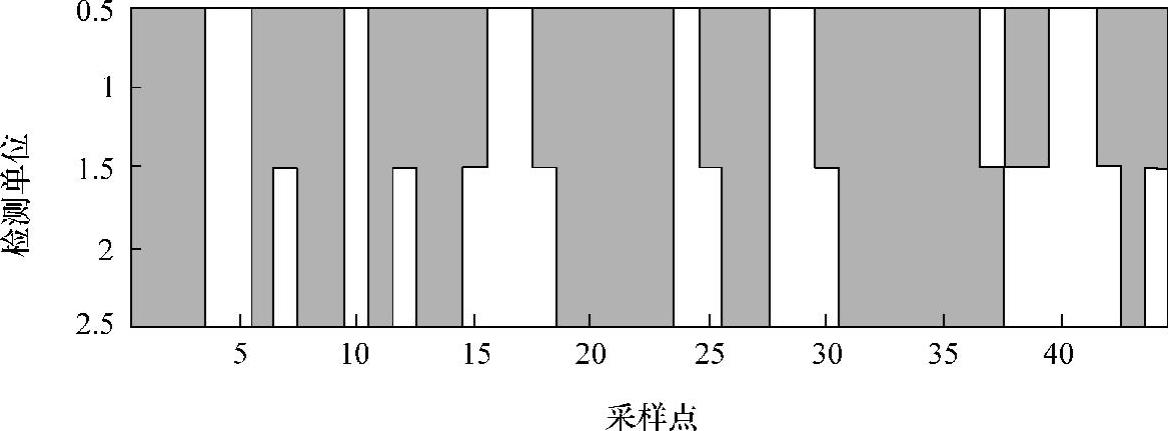
图8-21 差分阈值法分割得到的检测重要区域

（3）重要区域分割的动态范围阈值方法 使用差分阈值法分割重要区域存在一个缺点。图8-20中引线所指的区域也是重要的，但由于此范围内曲线呈缓慢变化的线性，差分值较小而没有被分割出来。因此在进行差分阈值分割的同时，还需要采用数据动态范围法分割。动态范围即一个数据块内每通道数据中最大值与最小值的差值。重要的漏磁信号具有较大的动态范围。表8-2为一些典型检测区域原始数据和差分数据的动态范围。

表8-2 原始数据和差分数据的动态范围

因此，如果块内各通道数据的动态范围大于一定的动态范围阈值，则这个数据块也是重要的。同时采用差分阈值法和动态范围阈值法得到的检测重要区域如图8-22所示，此时的分割更为准确。

图8-22 同时采用差分阈值法和动态范围阈值法分割得到的检测重要区域

在重要区域分割时，没有使用更为简单常见的幅度阈值，其主要原因是：由于各通道励磁强度、探头提离值及安装精度的不同，各通道的数据基线经常存在较大的差异。表8-3为图8-20中平坦区域内非重要数据块中10个通道的数据平均值，可见各通道的数据基线差值是很大的，因此不能采用幅度阈值法。

表8-3 非重要数据块中各通道的数据平均值

3.基于霍夫曼编码的压缩方法

经过重要性判断后，原始数据块被分成重要数据块和非重要数据块。非重要块内数据的主要特点是数据分布比较集中，反映在检测曲线上则是比较平坦，因此可以用一段直线代替。直接保存首列数据压缩率较低，采用的方法是对首列数据的差分值进行霍夫曼编码。首先保存数据块左上角即首行首列数据的值，然后计算首列数据的差分值，再对这些差分值采用改进的霍夫曼编码方法编码。其码字结构为C=（SSSS，附加位）。其中码字SSSS将差分值的幅度范围分为9类，幅度值类型设为B。附加位用以唯一地规定该类中一个具体的差值幅度。如果具体的差分值为DIF，则对DIF的编码规则为：若DIF≥0，附加位为DIF的最低B位；若DIF＜0，附加位为DIF补码的最低B位。这样，虽然不传DIF的符号位，但从附加位的最高位可以判断出数值的正负。这种编码方法的好处是：如果直接对差分值进行霍夫曼编码，则码表就有512项，而且表中的编码字长可达几十位以上。在硬件实现时，这样巨大的编码表甚至会耗尽FPGA中的查找表资源，而且也会给变长编码的凑整存储带来极大的困难。当然，节省资源的好处也有代价：相对于直接编码，这种方法的压缩比要低一些。

对于重要数据块，与上面的方法类似，在保存首列数据的基础上，对每行数据的差分值也进行霍夫曼编码。这样，可以实现对重要数据块的无损压缩。(www.xing528.com)

对实测漏磁数据，采用上述方法可以达到10∶1以上的平均压缩比。其优点是算法的硬件实现比较简单，实时性好；不足之处是由于需要保存块初值因而压缩比不高。

4.基于小波变换编码的压缩方法

（1）提升小波变换 虽然基于Mallat算法的小波变换相对于离散内积的方法已经得到了很大的简化，但Mallat算法中的卷积累加等运算还是比较复杂的。提升小波变换的实现过程更为简单，在变换时需要的存储空间更小。所有用Mallat算法实现的小波变换都可以转用提升格式来实现，而且可以用提升格式来构造新的小波。提升算法如图8-23所示。

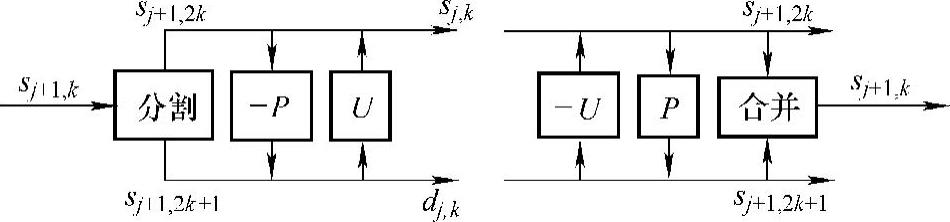
图8-23 提升算法

提升小波格式包括三个步骤：

1）分割/合并。分割即通过Lazy小波把信号分割成两个子集：奇数子集和偶数子集。合并则为分割的逆过程。

2）预测。所谓预测，就是用偶数部分来预测奇数部分，P表示预测算子，预测误差作为高通小波系数。预测过程是可逆的。

3）更新。更新就是用预测误差来更新偶数部分，U代表更新算子，更新的结果作为低通尺度函数系数。更新过程也是可逆的。

采用JPEG2000标准推荐的LeGall5/3滤波器组对漏磁数据进行变换，分解滤波器系数列于表8-4中。使用5/3滤波器组有两个优点。首先，5/3小波变换是完全可逆的整数操作，这样可以对重要区域进行完全无损地压缩；其次，5/3小波变换中不用乘法操作，而只需要移位及加法操作，这样可以节约大量的硬件面积和运算时间。

表8-4 5/3小波分解滤波器系数

（2）提升小波变化的处理流程

1）DC平移。在变换前首先将数据块中的每个数据都减去相同的值2^m，这样可以使小波变换时得到的系数较小，易于量化编码。由于漏磁采样数据精度为8位，此时m取7。

I（x，y）←I（x，y）-2^m （8-34）

2）边界延拓。为避免边界效应，要对小波变换前的数据进行周期对称延拓，其程序流程如图8-24所示。

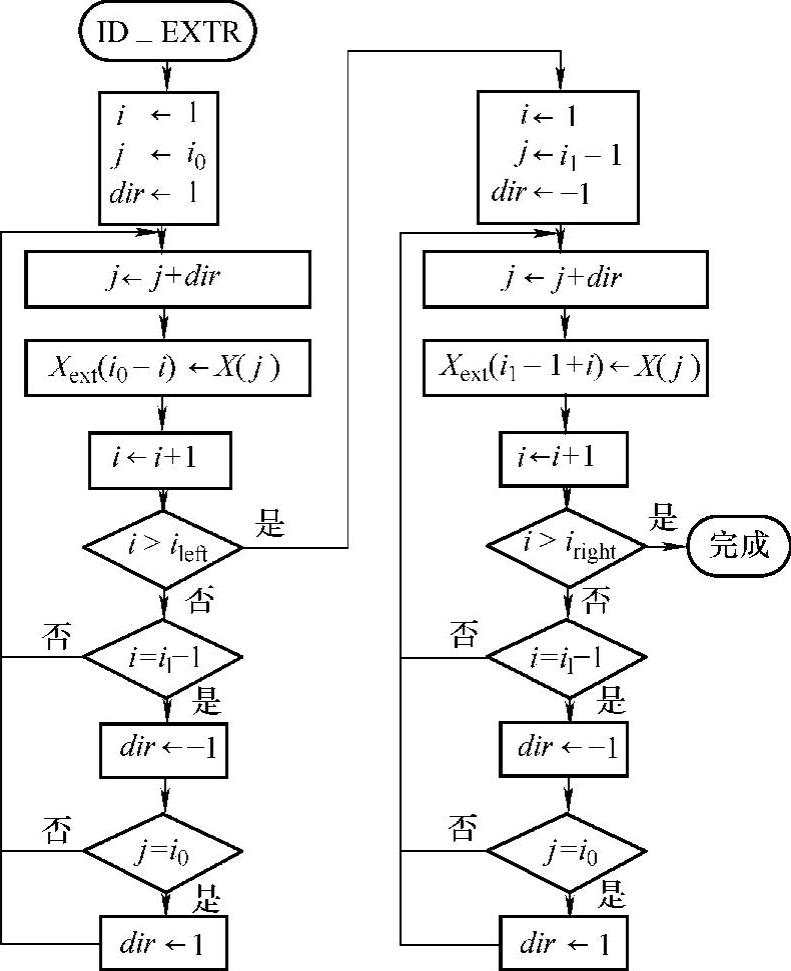
图8-24 边界延拓程序流程

3）一维提升变换。一维提升变换程序的流程如图8-25所示，数据经边界延拓后，进行提升处理。5/3小波的提升处理公式为

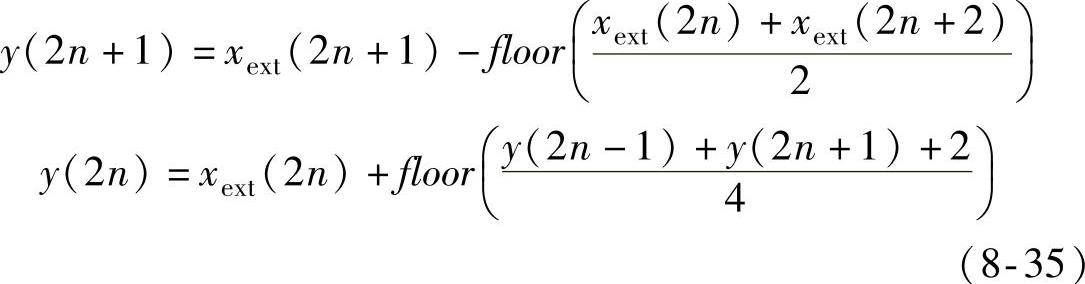
图8-25 一维提升变换程序流程

4）重排变换系数。提升小波变换后的变换系数是按原位存储在对应的奇偶位置上的，为了进行后续的变换和编码，需要把变换系数重排。重排变换系数程序流程如图8-26所示。

5）多级变换。对重排后的低频分量按上述顺序重复进行处理，就完成了多级的提升小波变换。

（3）SPIHT编码 分级树中的集合分裂（set partitioning in hierarchical trees，SPIHT）是一种非常优越的小波变换后系数的量化编码方法。它的主要特点是：运算复杂度低，编码效率高，能够实现嵌入式渐进编码。所谓分级树是指记录非重要系数的零树集合；非重要系数是指在量化过程中，小于某一量化阈值的系数。对于不同的量化误差级别，零树的结构是不同的。所谓集合分裂是指在量化误差由大减小的过程中，不断有重要系数从非重要系数的集合中分裂出来。SPIHT方法的基本要素包括：

1）依据系数幅值对非重要系数集合进行分裂的分类算法。

图8-26 变换系数重排程序流程

2）位平面的渐进有序发送。

3）利用频带间的自相似结构构造零树。

SPIHT算法的关键之处在于集合和系数重要性的判定，对集合和系数进行检测的顺序非常重要。算法中用三个列表来记录有关检测顺序的信息，它们是非重要集合列表（LIS），非重要像素列表（LIP），重要像素列表（LSP）。在两个像素列表中用坐标（I，j）记录像素位置；在集合列表中坐标（I，j）表示集合，并且记集合D（I，j）为A型，集合L（I，j）为B型。

通过控制SPIHT算法的量化层次可以方便地实现有损压缩和无损压缩。对于非重要数据块，量化到n=4时，压缩比可达20∶1以上；对于重要数据块则完全量化，压缩比为2∶1左右。

采用提升小波变换和SPIHT编码方法压缩漏磁检测数据，算法相对于霍夫曼编码方法要复杂得多，但SPIHT编码可以控制量化失真度，如果允许重要数据块压缩时存在微小失真，可以得到更大的压缩比，因而算法的扩展性更好。