中等精度光陀螺的长程曲线实验

1.中等精度光陀螺的长程曲线实验

实验采用中等精度光陀螺，精度为0.5°/h。解算所得轨迹用地理经、纬度表示如图7-21所示，实际轨迹的卫星地图如图7-22所示。解算轨迹经过修正后，终点位置的经纬度误差见表7-4。

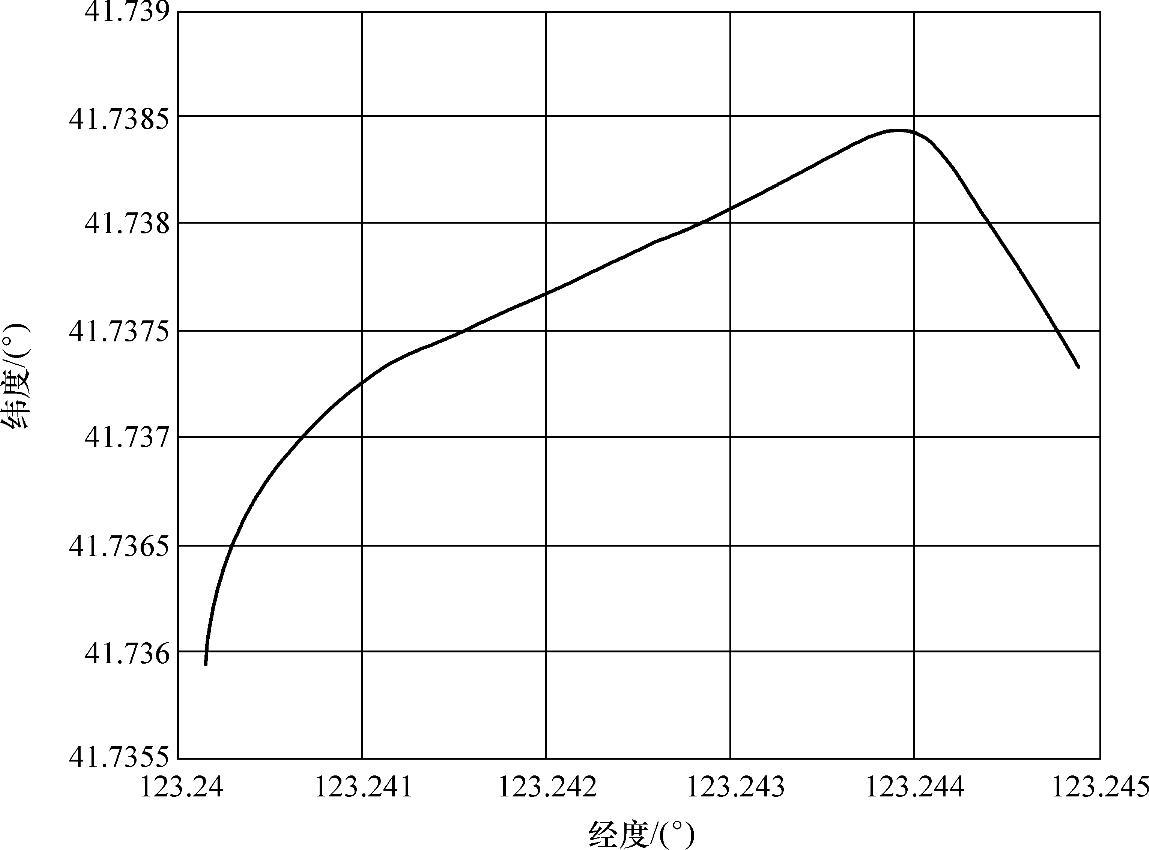
图7-21 经、纬度表示解算的600m轨迹解

图7-22 卫星地图上表示的600m实验轨迹

表7-4 终点导航解算信息与误差

由表7-4可以看出，对于600m的实验轨迹的测量，经、纬度误差均小于1″，里程误差小于被测量里程的1%。

对于实验图中绕隔离带位置，其地理坐标为北纬41.7375°，东经123.2417°。轨道漂移距离经测量为0.6m距离。在导航坐标系下表示如图7-23所示。

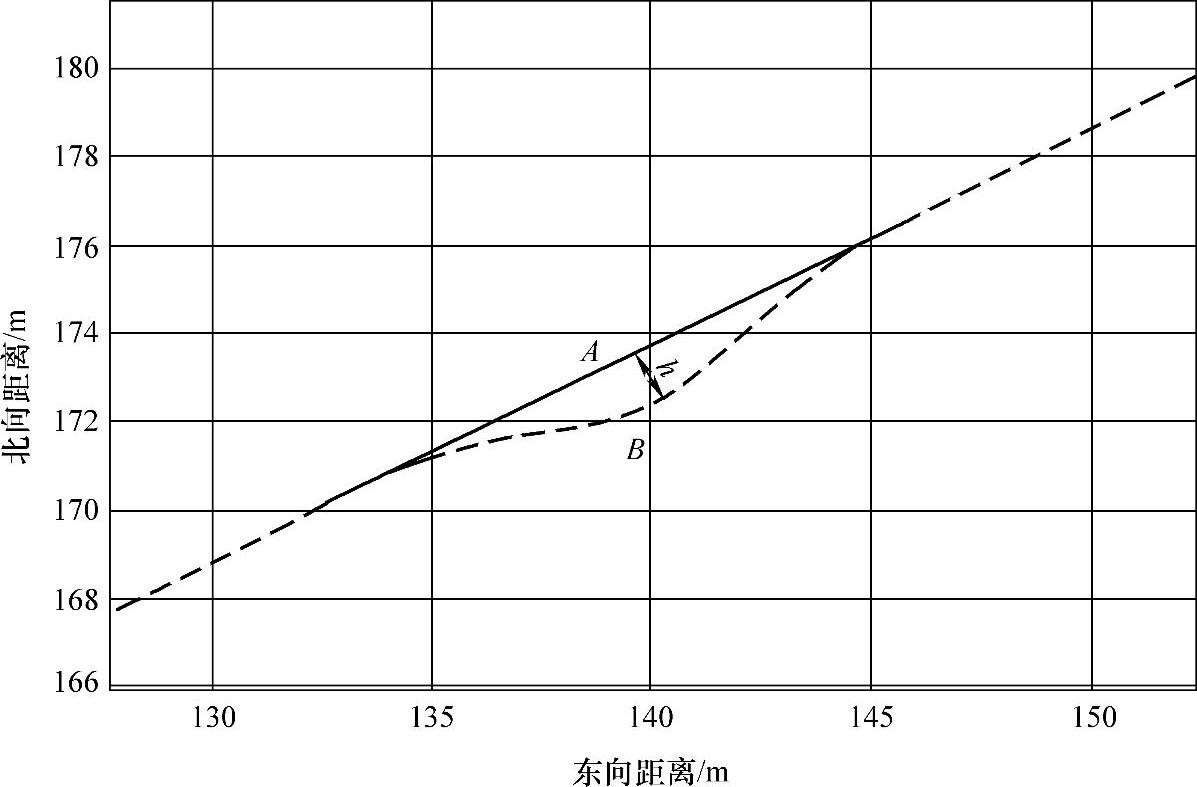
图7-23 实验中弯折的测量

图中表示的是解算得到的弯折点的轨迹，如虚线所示。A、B两点间的距离表示弯折的最大幅度。A点坐标为（139.2580m，173.3326m），B点坐标为（139.8115m，172.2290m），两点间距离为0.563m。实际轨迹中的弯折段测量得到的距离为0.592m。所以在长直轨迹的测量中，该方法依然能够实现对管道弯折等量的测量和定位。

2.中等精度光陀螺的长程环形轨迹实验

表7-5为实验轨迹的地理信息。

表7-5 实验轨迹地理信息

利用建立起来的误差模型，对测量误差进行修正。修正后，结合解算得到的姿态信息和里程轮测量得到的里程信息，对行进轨迹进行解算。对于平面运动，主要是对航向误差进行修正。图7-24所示为修正前后的航向角。

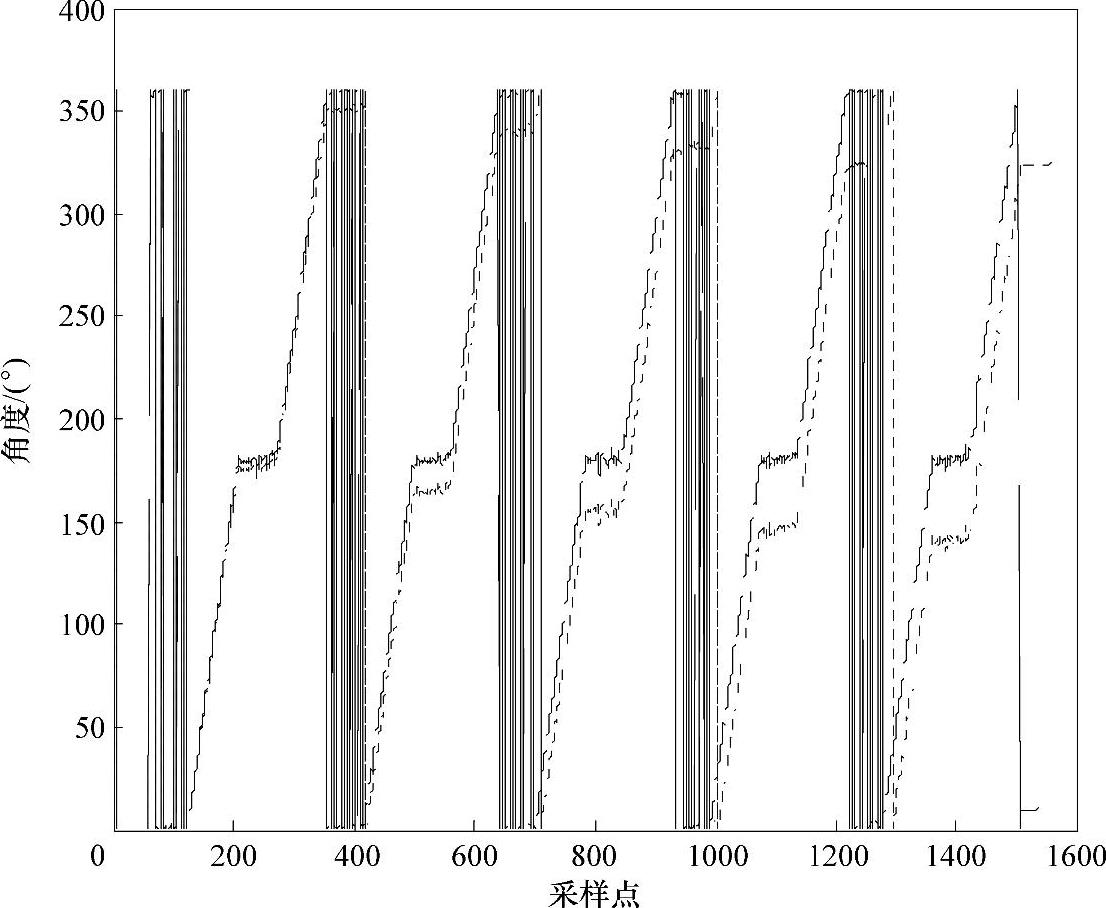
图7-24 修正前后的航向角

如图7-24所示，虚线为未做磁标记处分选修正的航向角解算结果，可以看出在修正前，由于陀螺仪的漂移误差，航向角误差不断增加，对于环形轨迹两直线段轨迹，航向角之差无法达到180°。修正后所得的环形轨迹的经、纬度表示如图7-25所示。

图7-25所示对应的卫星地图如图7-26所示。修正前后计算所得终点的经、纬度误差见表7-6所示。

经过修正，误差比率减小到0.16%，为修正前误差的8.2%。

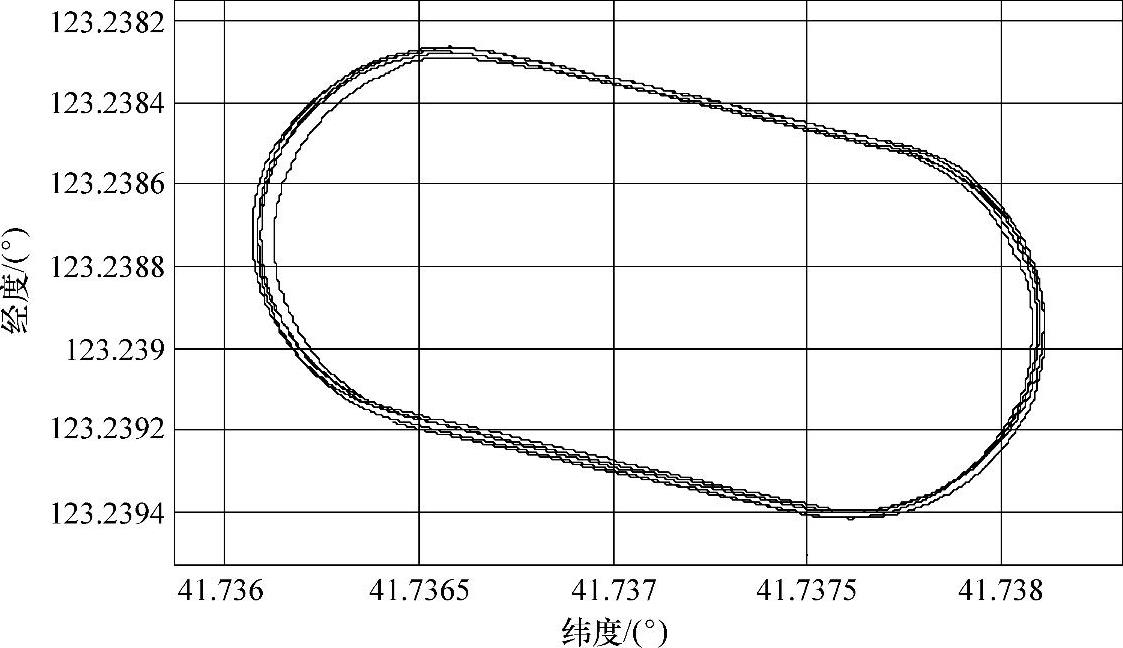
图7-25 经、纬度表示的修正后的环形轨迹

图7-26 卫星地图上的实验轨迹(www.xing528.com)

表7-6 经、纬度误差

3.高精度光陀螺的长程实验

高精度IMU元器件精度达到0.02°/h，相对于之前的中等精度光纤陀螺0.5°/h提高很多，但与公认的高精度IMU（可以自行指北）的精度0.005°/h相比还有不小的差距。

该试验平台依次经过采样点1～25，（采样点2～5形成一个近似半圆）形成封闭曲线，理想的惯性导航系统解算之后生成的轨迹应封闭，实测采样点1和25之间的距离为判断算法精度的重要依据，如图7-27所示。

实际解算情况如图7-28所示。

因为试验最初的经、纬度信息来自于谷歌地图，因此实际解算的经、纬度没有测绘价值，解算轨迹的相对位置信息是主要的考察对象，尤其是封闭点距离（1点和25点之间的解算轨迹图上的距离）体现了整体算法的精度（xy平面达到5m以内）。显然，实验解算图起点与终点基本吻合，里程共计1854m。俯仰角安装误差暂未考虑。相关技术参数如图7-29～图7-32所示。

图7-27 长程管道定位试验载车运行轨迹

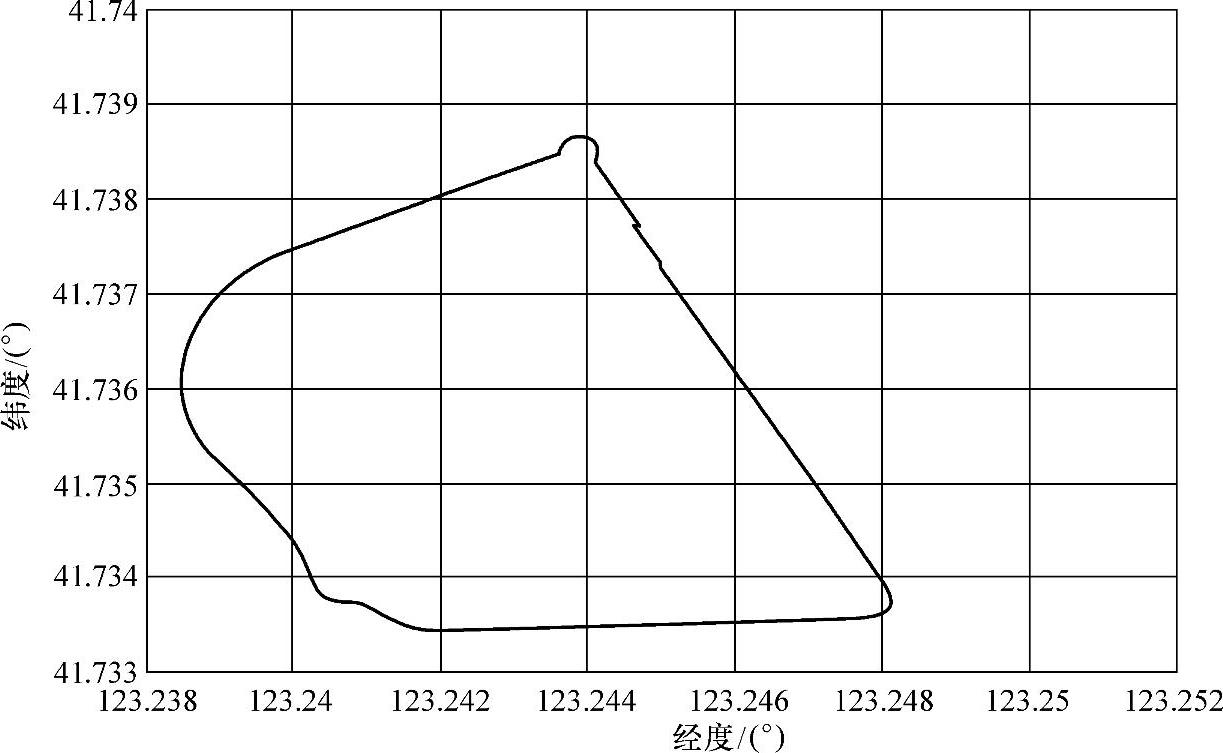
图7-28 高精度惯性导航系统长程实验解算轨迹图（经、纬度表示，xy平面）

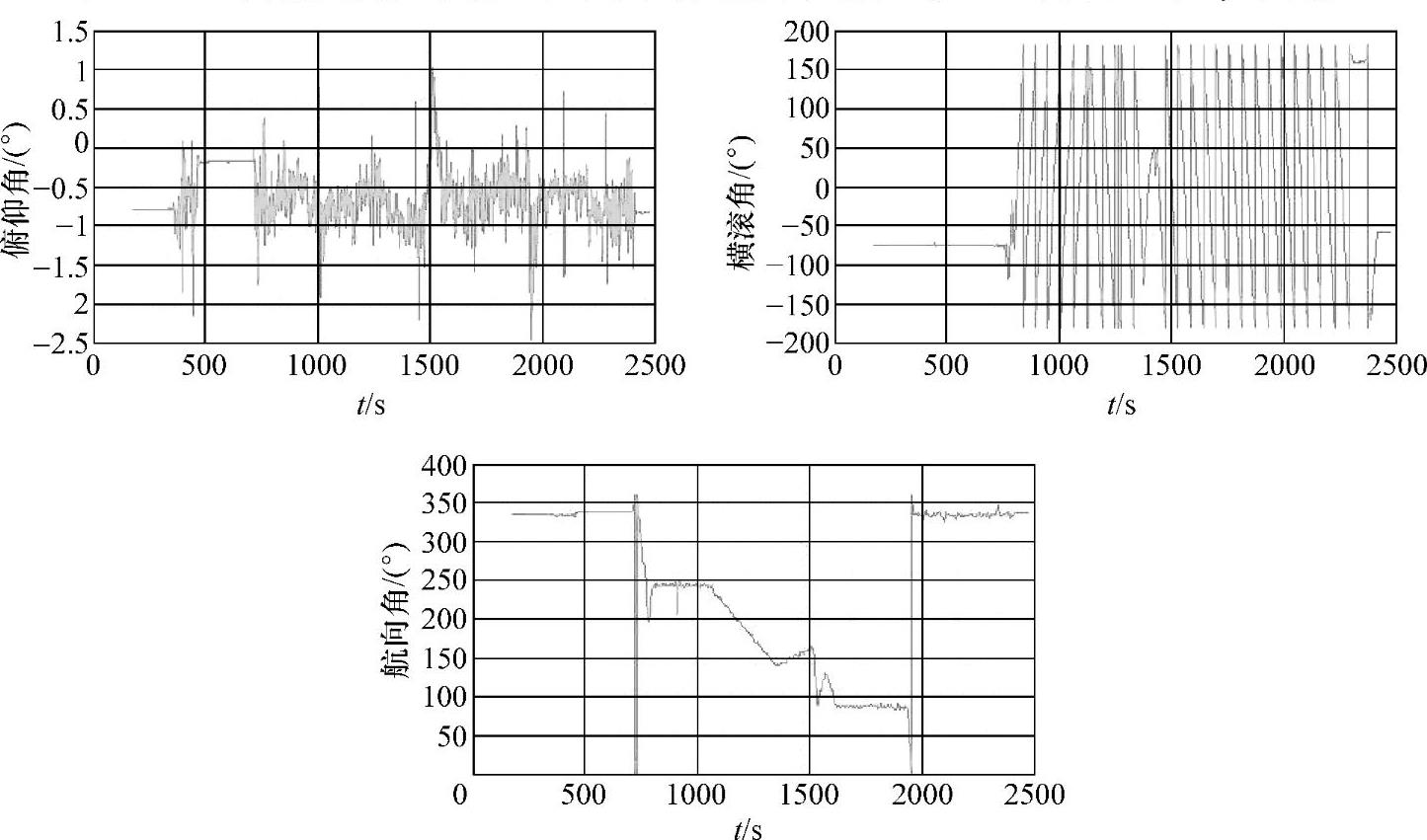
图7-29 导航全程姿态信息

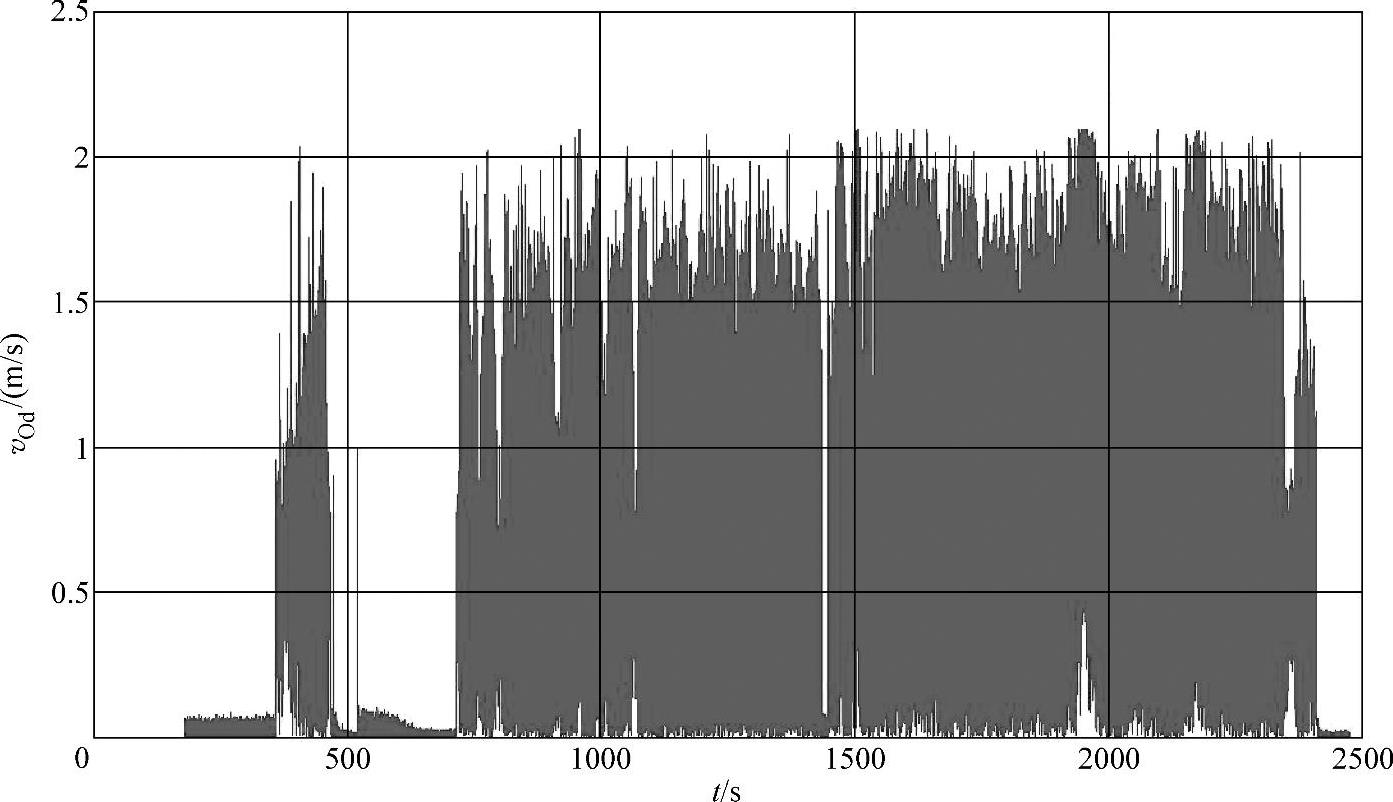
图7-30 导航全程里程轮速度输出信息

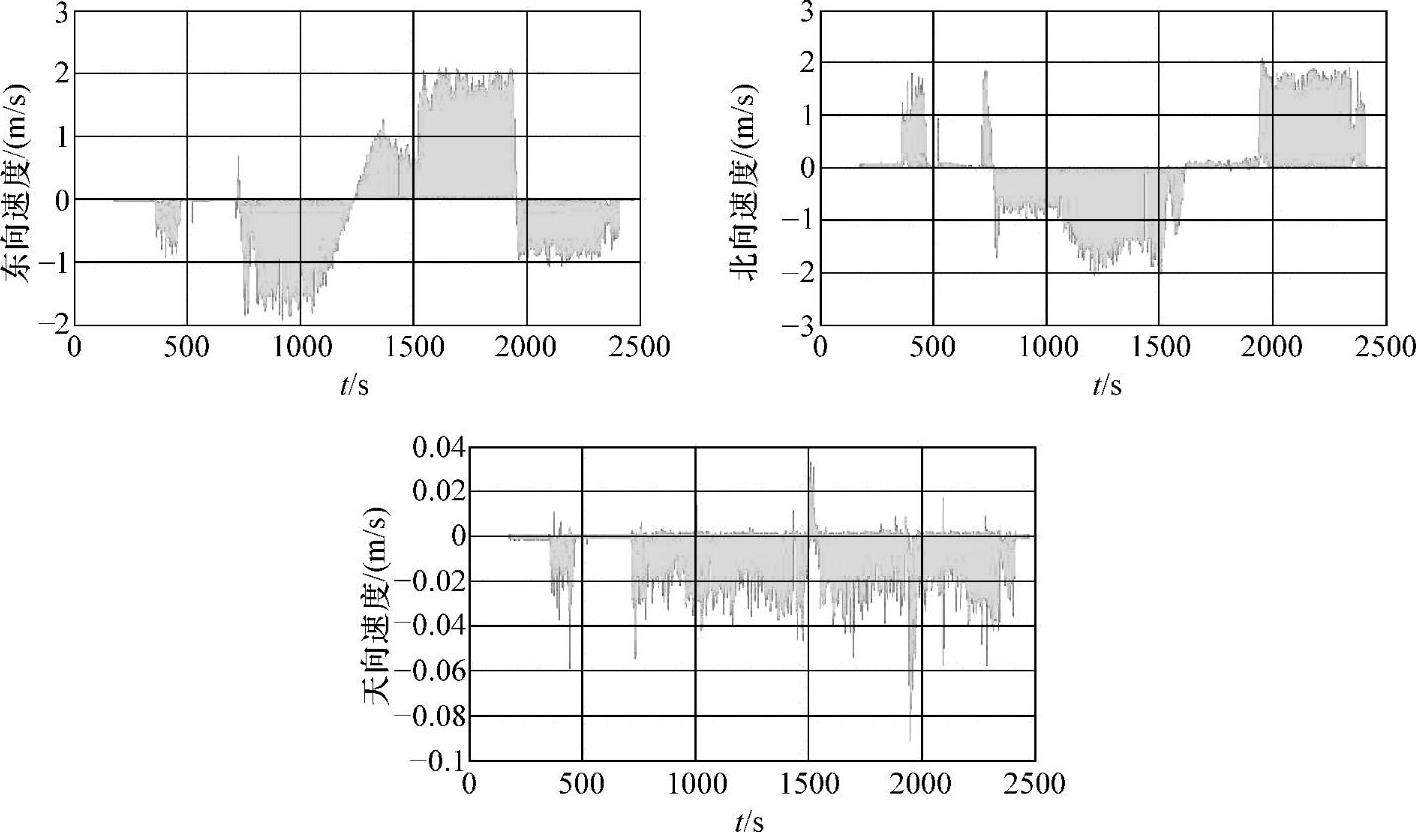
图7-31 导航系统东北天速度信息

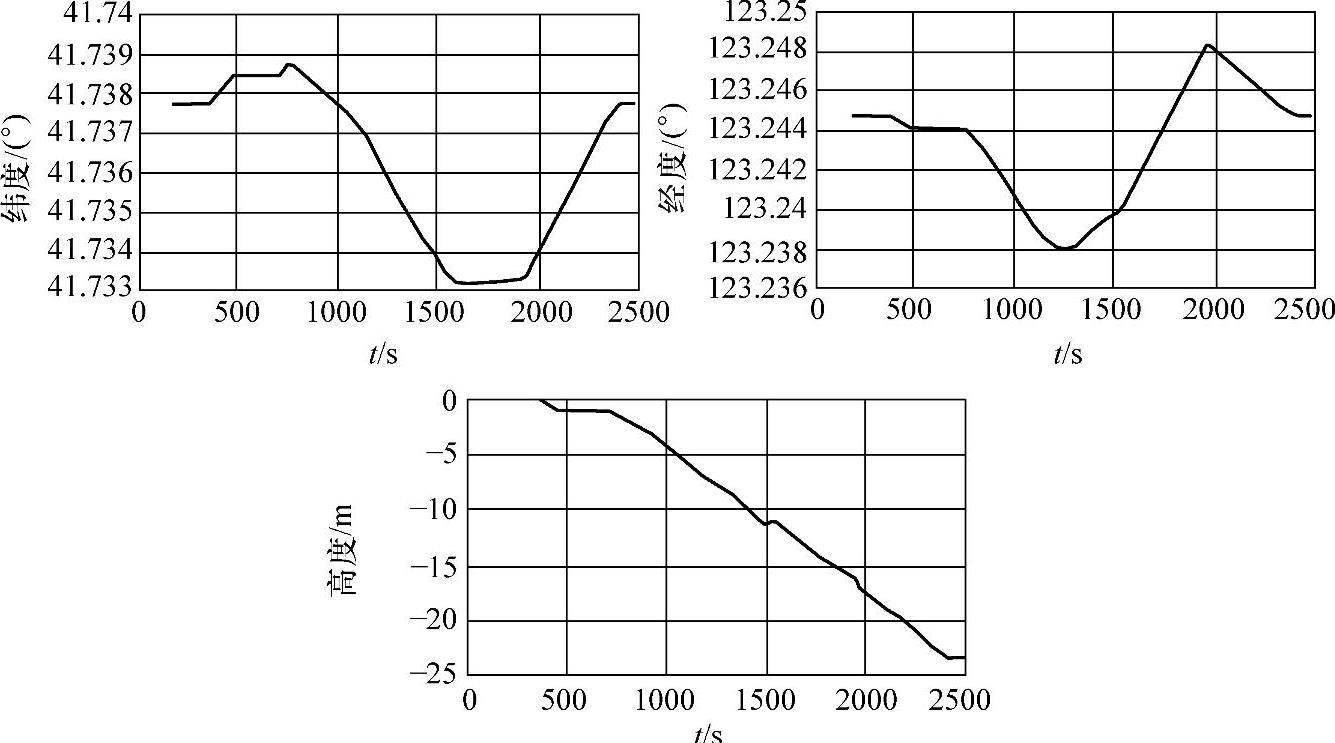
图7-32 导航系统位置信息

在上述解算中没有考虑系统安装过程中俯仰角的安装误差，而该误差从第一个采样周期开始参与解算和迭代，是造成高度信号误差较大的主要原因。因此在导航解算中人为地加入了4°俯仰角安装误差（该误差因素必然存在，在不同试验平台有不同的体现，这里人为加入的是估计值，更准确的估计算法还需继续研究），使解算精度得到较大提高，尤其是高度通道数据（俯仰角、天向速度、高度等）产生了明显的收敛，其他指标也得到改善，系统导航结果如图7-33～图7-35所示，可与图7-29、图7-31和图7-32进行对比。

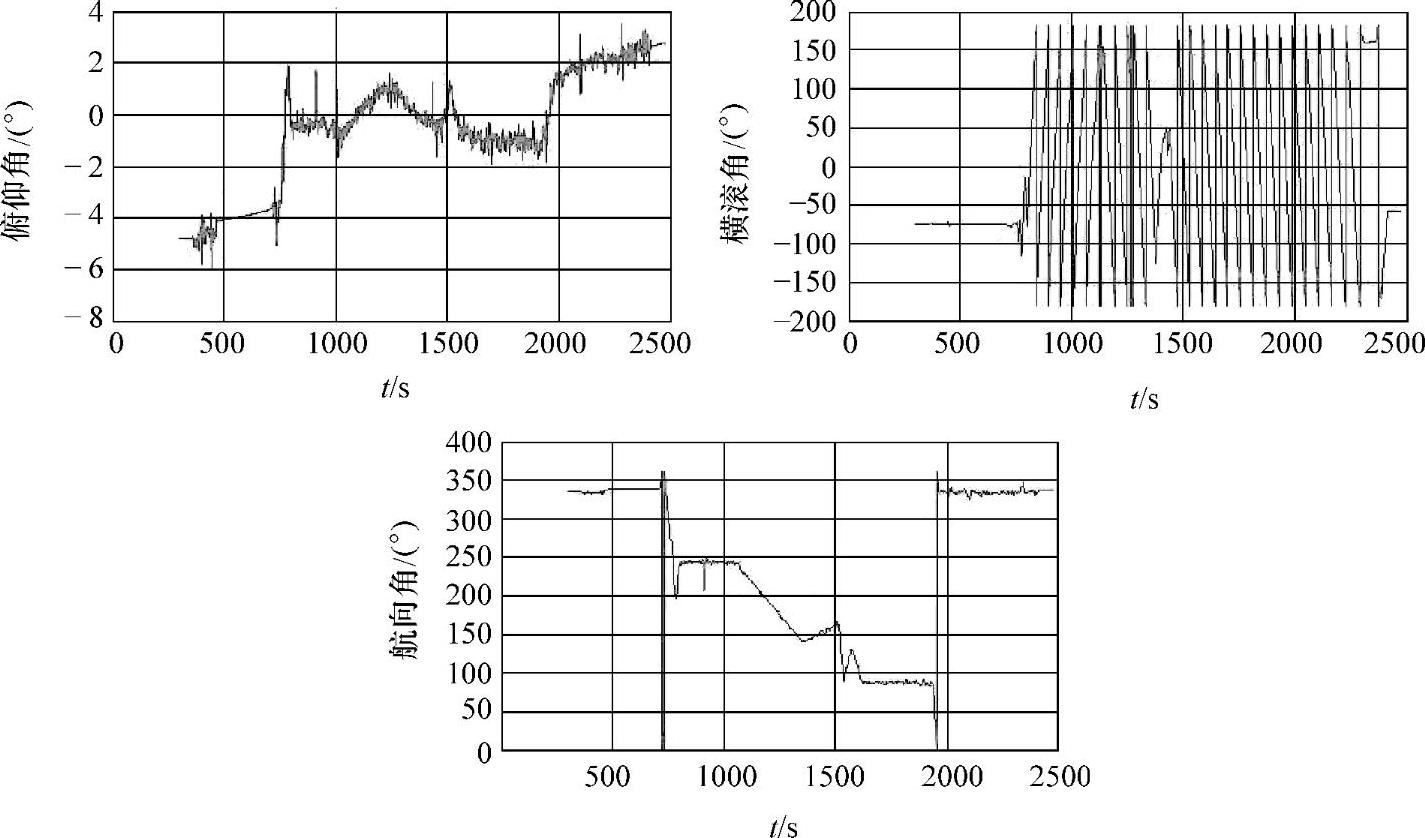
图7-33 导航全程姿态信息（加入4°俯仰角安装误差）

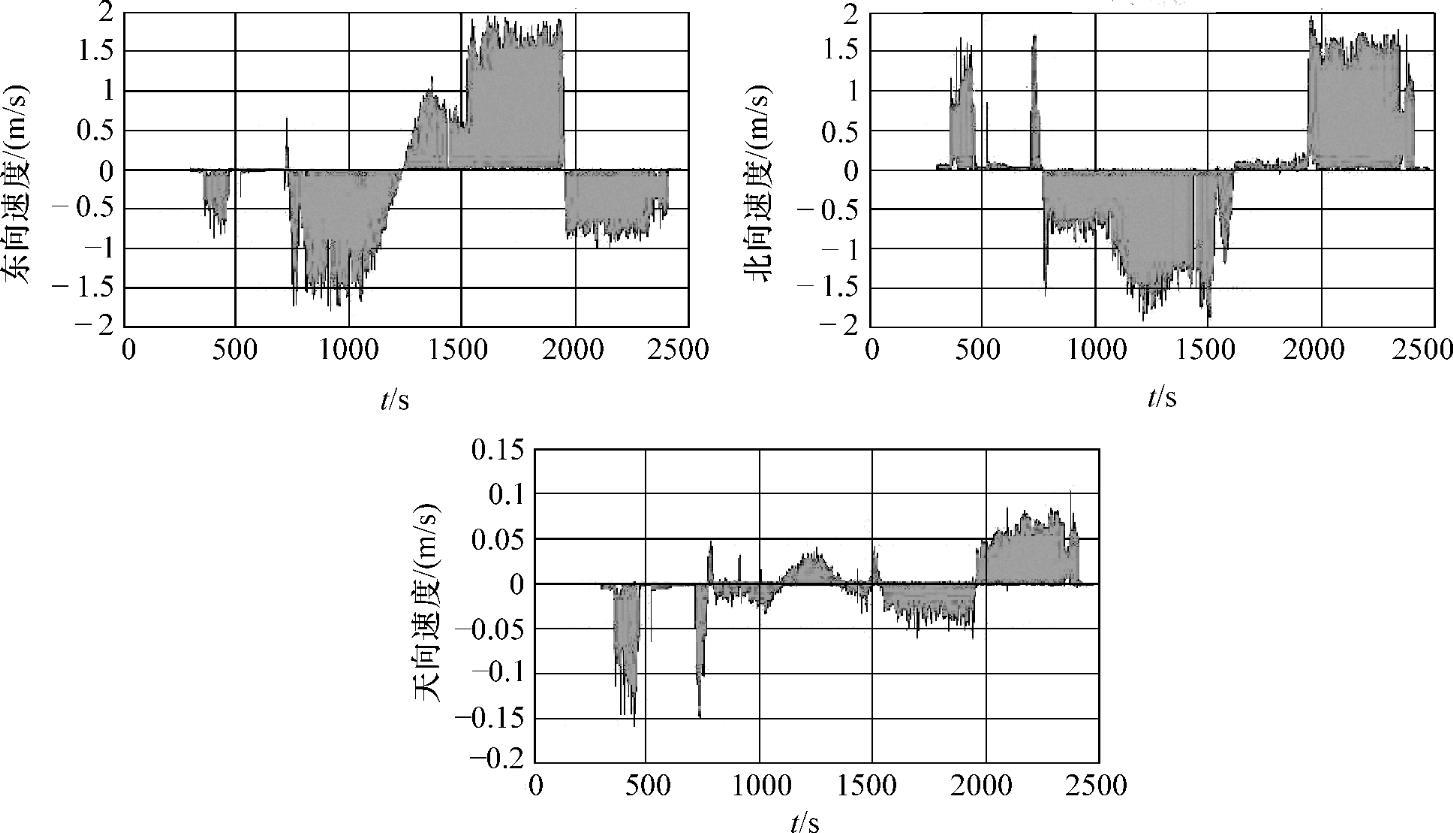
图7-34 导航系统东北天速度信息（加入4°俯仰角安装误差）

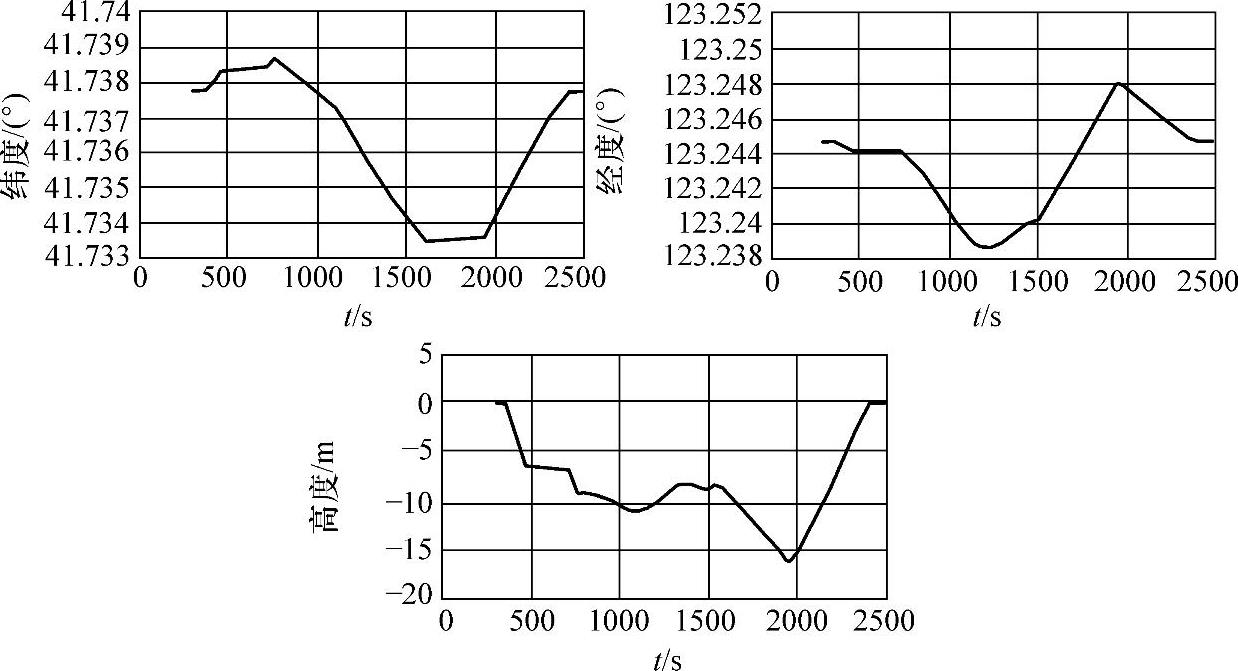
图7-35 导航系统位置信息（加入4°俯仰角安装误差）