磁标记在长输管道内检测中的实际应用

大多数管道内检测项目中，管道上间隔若干距离会设置地理磁标记来帮助PIG进行定位。磁标记已经成为管道内检测中的重要辅助定位工具。在磁标记位置，管道的具体地理定位信息是可以通过地上测量获得的。这些信息包括：该处的管道地理位置，即经度φ_k和纬度λ_k，埋地深度h_k，距初始点的航行里程D_k。除此之外，因为磁标记和里程桩多设置在直管段位置，因此，可以通过确定管道的走向来确定经过磁标记位置时，PIG的航向角ψ_k。下标k表示经过的第k个磁标记位置时的数据。

获得了以上数据，就可以对陀螺仪、加速度计和里程轮进行误差建模，实现分段修正的目的。分段修正的过程是先按段对导航数据进行解算，将解算所得到的结果和经过地理磁标记的中间点的时刻进行对准。时间对准后，可以判断出通过该中间点时，地理坐标解算系统计算得到的位置信息。将该信息同磁标记地上测量的位置信息进行比较，得到位置和姿态的偏差。再利用偏差值，对传感器的误差模型中的参数进行估计，得到该段路径内传感器的误差模型参数。最后利用该模型对原始数据进行分段修正。分段修正方法原理如图7_-16所示。

图7-16 定位误差在磁标记处分段修正原理

因为惯性导航的误差具有随时间积累的特点，所以对于累积误差，只能通过外部数据对其进行纠正和消除。管道深埋于地下，无法应用类似于GPS等辅助导航方式进行累积误差消除。因此，应用磁标记处所提供的导航信息进行分段式误差修正对于PIG上的捷联惯性导航系统来说，具有实用性和工程上的意义。下面介绍捷联惯性导航系统所应用传感器的误差模型，以及应用磁标记的地理信息进行分段修正的方法。

对导航误差进行修正，必须在获得一定外部辅助信息的情况下才能够对误差模型的参数进行估计。磁标记和里程桩作为管道铺设的基础设施，已经广泛地应用在管道建设中。对于一些建设较早的管道，也通过后期的里程桩维护，在相应地点埋设了磁标记。磁标记的磁场信号会被PIG的漏磁传感器检测到，并记录下通过时间。这样就可以应用地面上获取磁标记处的管道地理信息对传感器数学模型进行参数估计，进而应用误差模型，消除惯性导航过程中的误差积累。

1.利用加速度信息对里程解算速度进行即时修正

加速度计的解算结果可以有效地反映往复运动的运动特性，即对于短时间内的运动特征，其精度是可以应用于速度信息辅助计算的。为此，结合里程轮的测量原理，提出一种不直接利用加速度计进行速度解算，而是按照里程周期，利用加速度信息提高里程速度的实时性的速度解算方法。

因为PIG在管道中运行，不存在横向的位移和速度，即速度的方向始终沿着机体坐标系的y轴方向，因此该方法只需利用y轴轴向的加速度信息，对里程轮所采集信息计算得到的里程距离内的平均速度进行实时处理。里程轮转动一周所经过的时间称为一个里程周期，用t_o表示，里程轮的周长称为一个里程距离，用D表示。里程轮转过一周只产生一个脉冲。设一个里程周期的起始和终止时刻为t₁和t₂，可以计算t₁～t₂时间内的平均速度v_A12为

应用里程轮取代加速度计进行速度求解，可以抑制加速度计引起的速度误差的累积，但是里程速度的瞬时精度较低。为此在一个里程周期内，利用加速度对平均速度进行修正的公式为

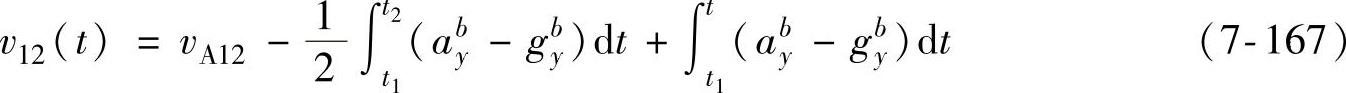
式中，v₁₂（t）为t₁～t₂时间内PIG速度；a_y^b为机体坐标系y轴上加速度值；g_y^b为重力加速度在机体坐标系y轴上的分量。

利用该修正公式在不改变里程周期内平均速度的同时，可应用加速度进行瞬时速度求解。其中只选用y轴加速进行计算是由于PIG在管道中运行时，只存在y方向的直线运动。

2.利用磁标记处的地理信息对陀螺仪误差模型参数进行估计

在磁标记处，应用里程桩提供的管道地理信息估计模型参数。确定参数后的模型用来修

正量测值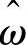，实现姿态误差的修正。

由于零偏误差σ₀具有稳定性，可通过对检测开始时的静止段数据求均值来进行估计。在磁标记位置，地下管线通常为长直段，因此角速度的测量误差以时间相关误差为主。时间相关参数k_t的估计可表示为

式中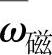，为磁标记处角速度平均值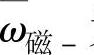；为经过上一个磁标记位置时的角速度平均值；t、t_-分别为PIG通过当前磁标记和上一个磁标记的时刻。(www.xing528.com)

由于姿态角与加速度之间有如下关系：

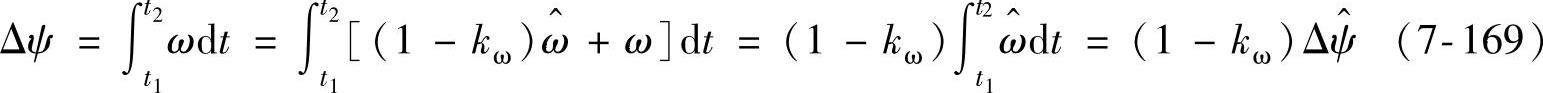
式中，Δψ为通过磁标记t₁和t₂处管道姿态角变化；ω为角速度真值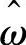；为零偏误差的时间相关误差修正后的陀螺仪输出角速度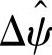；为由检测设备输出角速度解算得到的对应量。由式（7-169）可得

通过该标度因数误差参数的估计建立起完整的陀螺仪误差模型，在三维轨迹解算中进行分段误差修正，减小轨迹误差。

3.对里程轮误差进行修正

对于长输管道内检测作业，里程轮误差的产生主要有两方面因素：一是受管道内运输介质的润滑作用影响而引起的里程轮打滑，通常造成里程数小于实际值；二是由于长输作业引起的里程轮磨损、半径逐渐减小而造成里程数大于真实值。

里程轮在地理磁标记处获得管道的相对里程，以实现在中途的分段里程误差修正。在管道检测结束后，应用测量的里程轮直径变化对里程误差进行估计。此时必须设计里程轮的误差模型。

里程轮打滑通常发生在法兰盘和直焊缝位置。根据管道安装标准，对于长输油气管道而言，法兰和焊缝的分布可以认为是均匀的。因此，以一阶函数为里程轮滑动误差建立模型为

所以里程轮刻度误差参数表示为

式中，ΔM为经过相邻磁标记之间的里程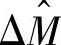；为由里程轮数据计算得到的两磁标记间的里程距离。

显然，根据磁标计实测距离，ΔM已知，由此可以求得k_m，进而修正里程轮误差。

里程轮的磨损主要是由PIG在管道中的横滚运动引起的，为了减小里程轮直径对里程和速度解算的影响，分别对检测前后的里程轮直径进行测量，建立基于横滚角速度的误差模型为

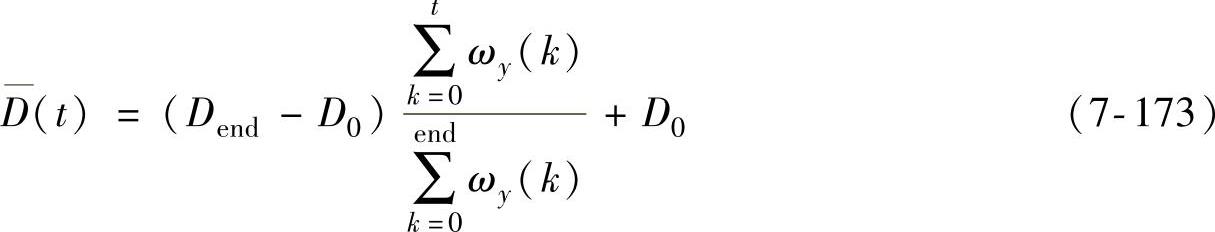
式中，D为直径，下标0和end分别为起始时刻和终止时刻；ω_y为y轴角速度。

该模型确立了里程轮半径与横滚运动的关系，可用横滚角速度对里程轮半径的变化进行估计。