信息融合技术在捷联惯性导航与里程轮组合导航系统中的应用

组合导航中应用里程信息对惯性导航系统误差进行抑制，不仅可以用来进行导航信息融合，同时可以实现导航数据测预处理。

算法原理是：将里程增量作为观测值，将状态误差作为状态量，利用卡尔曼滤波估计状态误差，采用里程校正方法对管道定位的SINS计算进行误差补偿。算法的功能图如图7-13所示。

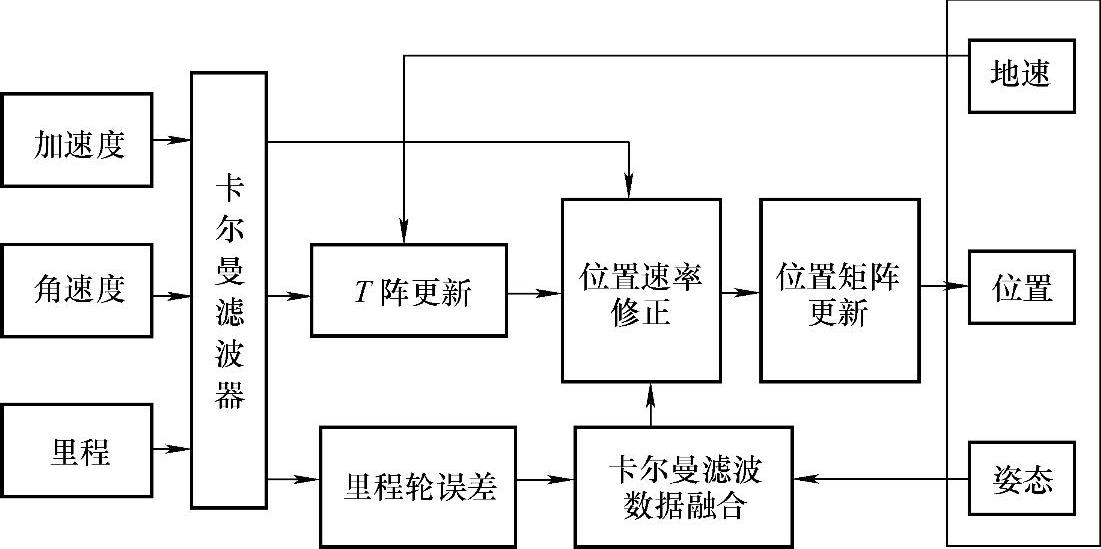
图7-13 组合导航算法功能图

在位移计算前对状态误差进行补偿，姿态误差为计算坐标系（c系）与实际导航坐标系的转换矩阵，可以用C^c_n表示，即

对姿态矩阵的误差补偿表示为

C^b_n=C_c^bCc_n （7-141）

估计出姿态误差角后，利用式（7-141）可以对姿态误差进行补偿。速度和位置补偿方法为

S_t=M_t-Δ_t （7-142）

式中，S_t为速度和位置的真实值；M_t为SINS的计算值；Δ_t为卡尔曼滤波的误差估计值。利用误差补偿方法对各状态量进行修正。

建立卡尔曼滤波方程，将n系下的姿态、速度和位置误差作为状态量X，并且不同于其他惯性导航，由于采用低精度传感器，将里程轮和惯性传感器的尺度因数误差忽略不计，管道地理坐标测量系统状态量取9维，可表示为

X=ϕ_xϕ_yϕ_zδv_nxδv_nyδv_nzδLδλδh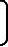 （7-143）

式中，δv_nx、δv_ny、δv_nz为PIG速度误差；δL为纬度误差；δλ为经度误差；δh为高度误差。

因为元器件精度较低，忽略其随机常值漂移和尺度因数误差。PIG运动示意如图7-14所示。

PIG只能沿管道向前运动，无法向上和沿侧面移动，因此PIG在b系的速度方向为：PIG的y向速度与里程轮速度相同，而x和z方向的速度为0，所以管道中运动的载体在b系的速度矢量可以用0 v_o 0^T表示。将里程轮速度转换到n系，即(www.xing528.com)

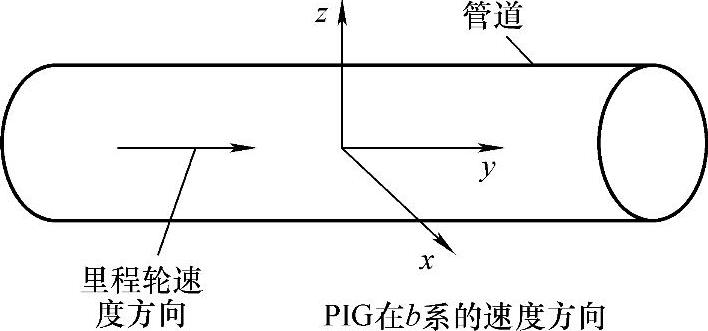
图7-14 PIG运动示意

V_no=Cⁿ_b0 v_o 0^T （7-144）

式中，v_o为里程轮速度；V_no为通过里程轮测得的n系下的速度，将其与惯性导航计算的速度之差作为观测值Z，即

Z=V_n-V_no=Δv_x Δv_y Δv_z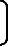^T （7-145）

根据状态量和观测值建立卡尔曼滤波微分方程为

式中，F（t）为状态微分方程系数矩阵，由式（7-29）、式（7-37）、式（7-42）、式（7-43）和式（7-44）推得；L为白噪声系数矩阵；H为观测矩阵，且H=0_3×3 I_3×3 0_3×3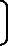；W为状态噪声矢量，即元器件的零偏噪声，且W=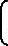ε_nxε_nyε_nz ▽_nx ▽_ny ▽_nz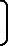，V为观测噪声矢量，即里程轮输出的速度误差，且V=δv_onxδv_onyδv_onz。

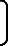W和V为高斯分布白噪声，它们与X之间两两互不相关。将式（7-146）、式（7-147）进行离散化处理得

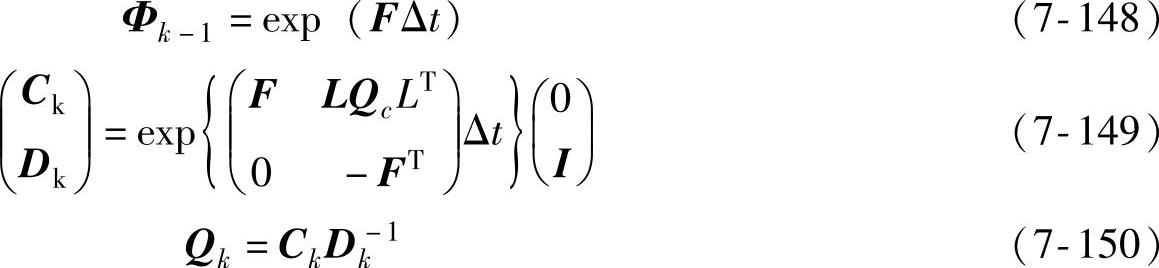
式中，Δt为卡尔曼滤波的计算周期；Q_c为W的方差矩阵；Q_k为W_k的方差矩阵；C_k和D_k分别为方差矩阵和转置方差矩阵。

因此得到卡尔曼滤波状态方程和观测方程为

X_k=Φ_k-1X_k-1+LW_k （7-151）

Z_k=H_kX_k+V_k （7-152）

式中，Φ_k-1为卡尔曼滤波的状态转移矩阵。