1.捷联惯性导航系统初始对准概述
在惯性导航系统进入正常工作状态之前,必须解决积分运算的初始条件、姿态角的确定、陀螺漂移的确定等问题。初始条件包括初始速度和初始位置,在静基座条件下,初始速度为零,初始位置即当地的经纬度和高度。给系统的初始速度即位置赋值的操作过程很简单,只要将这些初始数据输入计算机即可。初始调整是使平台坐标系与导航坐标系重合。
惯性导航系统是一种自主式导航系统。它不需要任何人为的外部信息,只要给定导航的初始条件(如初始速度、位置等),计算机便可根据系统中惯性敏感元件测量的比力和角速度实时地计算出各种导航参数。由于平台是测量比力的基准,因此平台的初始对准非常重要。惯性导航系统的初始对准就是在惯性导航系统尚未正式进入导航工作状态之前,建立导航状态所必需的初始条件。显然,初始对准的精度对系统以后的正常工作性能将产生直接的影响。
对于捷联惯性导航系统,由于捷联矩阵起平台的作用,因此导航工作一开始就需要获得捷联矩阵的初始值,以便完成导航任务。显然可以看出,捷联惯性导航系统的初始对准就是确定捷联矩阵的初始值。下面简要分析捷联惯性导航系统初始对准的特点。
首先,有大的初始不对准角。捷联惯性导航系统因为直接安装在载体上,其不对准角由载体的姿态和航向决定,一般来说不可认为不对准角值小,这就带来处理上的麻烦。事实上捷联惯性导航系统初始对准的目标只是测定惯性测量系相对于导航坐标系的方向余弦矩阵,即姿态矩阵。
其次,要测定瞬时方向余弦矩阵。捷联惯性导航系统与平台系统的一个重要差别是前者在初始对准时,必须求出瞬时方向余弦矩阵,这是因为对于捷联惯性导航系统来讲,载体的角运动不能被物理上隔离,随之而来的是在捷联惯性导航系统初始对准过程中还必须测量上述载体运动对误差角速度测量精度的影响,这一点往往比测量瞬时方向的余弦矩阵还要困难。
最后,捷联惯性导航系统可以有更多的可用信息。对于平台惯性导航系统,只有加速度计的输出才可以直接用于初始对准,陀螺仪的输出要求提供平台稳定回路,而沿平台轴的输出信息只能从同位器获得,但同位器的分辨率太低,不能满足初始对准的精度要求。与此相反,捷联陀螺的信息具有极高的角分辨率,可以直接用于初始对准。
2.管道惯性测绘工程中的初始对准技术
管道内检测作业中,PIG在开始检测前,通常在发球筒内停留较长的一段时间,因此应用于PIG上的捷联惯性导航系统可以实现在静基座下进行初始对准。
在静基座下,惯性测量单元测得的惯性参数为与所在位置的地球重力加速度方向相反的加速度-gb,陀螺仪测得的角速度为所在位置地球自转角速度ωbie在机体坐标系三个轴向上的分量。除了在南北极点位置,重力加速度方向应和地球自转角速度方向不重合。因此可以利用ωbie和-gb测量值和实际在该地理位置导航坐标系下的理论值之间的坐标变换进行求解,计算所得即为载体的捷联矩阵T。在对准的过程中通常采用一定的滤波技术去除传感器误差。
为了解决初始对准问题,必须结合管道内检测施工的实际情况。管道内检测器发射原理如图7-10所示。
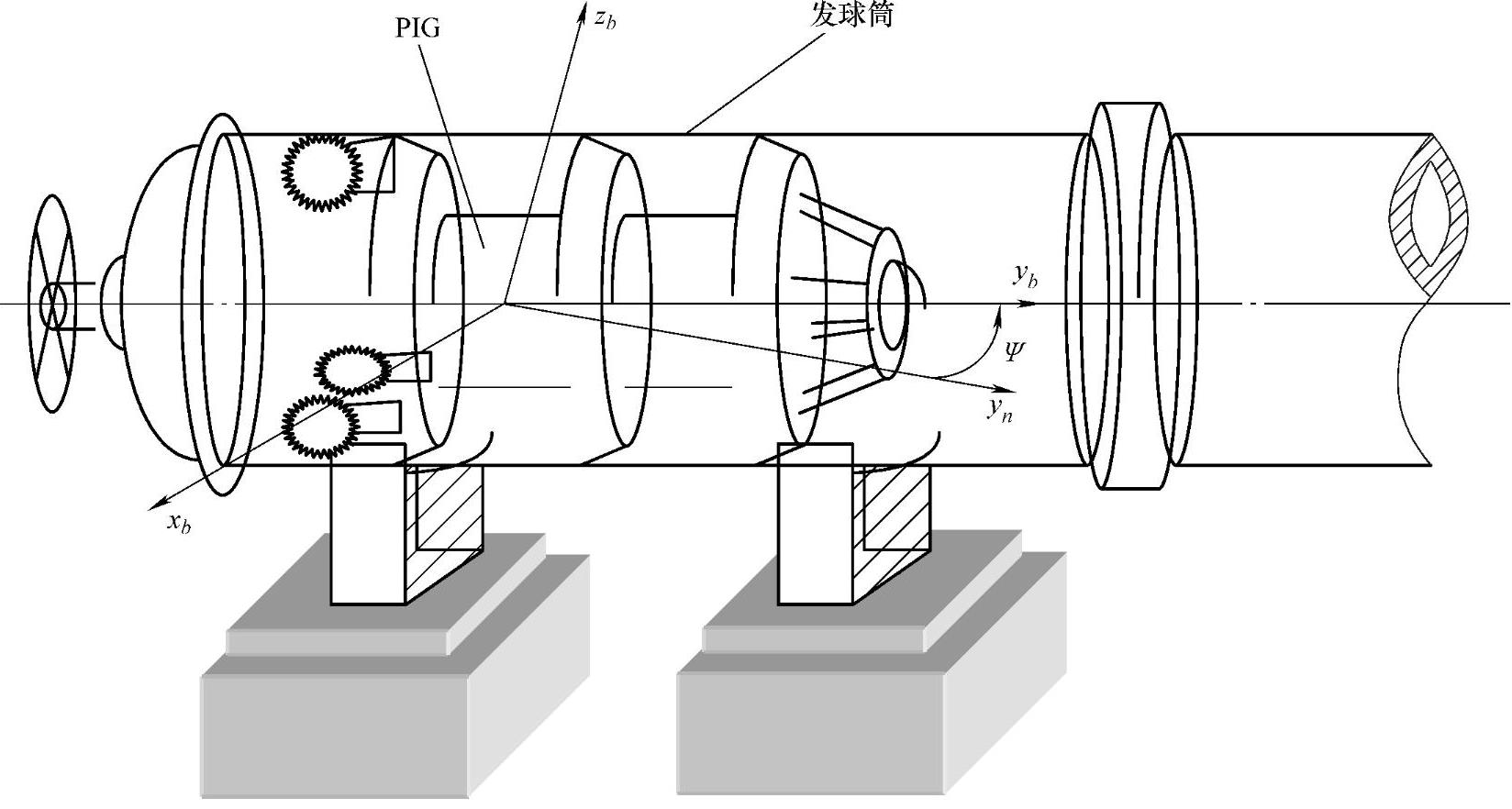
图7-10 管道内检测发射原理
加速度计测量的重力加速度只能提供一个方向的参考值,无法实现确定机体坐标系和地理坐标系的变换关系的初始对准。如图7-10所示,PIG在发球(投送管道内检测器)时,会在发球筒内静止较长的一段时间(约30min)。这段时间内,IMU单元可以测量大量的静止数据来进行初始对准。而且发球筒是相对于地面固定的,PIG在管道内保持一个固定的位置,所以可以采用地面测量的方法获取航向角。由于PIG和发球筒处于平行位置,测量发球筒方向角就可以确定PIG的航向角。在发球筒外,利用地上测量方法,精确地对发球筒的方位进行确定,并以此作为航向角ψ。PIG的俯仰角和横滚角可利用加速度计对重力加速度进行测量来确定。
根据所应用的姿态角的选取方法,取得捷联惯性导航矩阵的旋转顺序为先旋转横滚角γ,然后旋转俯仰角θ,最后旋转航向角ψ。航向角ψ为最后绕z轴进行旋转而确定的角度。因此,先利用重力加速度对俯仰角θ和横滚角γ进行对准。当俯仰角θ和横滚角γ确定后,机体坐标系按照这两个角度进行旋转,所得结果是机体坐标系xy平面必然同导航坐标系xy平面相平行,此时航向角ψ正是由水平测量所得到的发球筒的方位角。根据这种对准原理可用如下方程进行描述。
加速度计测得的对准加速度信息可以表示为(https://www.xing528.com)

重力加速度在导航坐标系下应表示为

先沿y轴旋转横滚角γ,横滚角旋转的结果是机体坐标系下的重力矢量移动到旋转后的坐标系的yz平面内,公式为
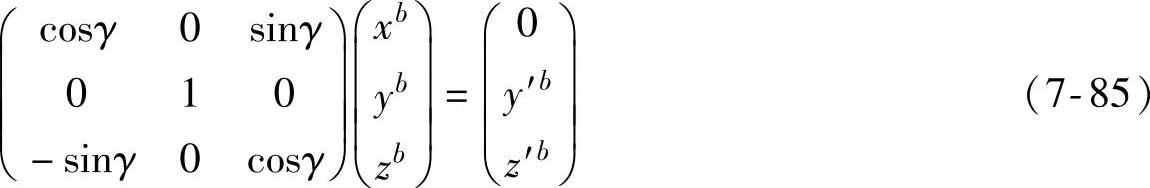
通过式(7-85)可以对横滚角γ进行求解,表示为

初始对准时的横滚角真值见表7-3。
计算得到横滚角后,对俯仰角进行计算,公式为

解方程式(7-87)可以得到俯仰角,表示为
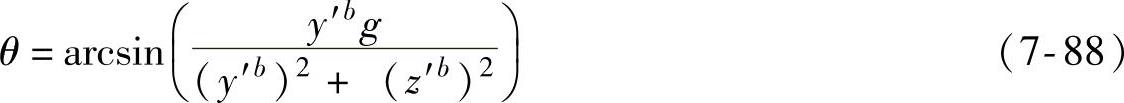
表7-3 初始对准时的横滚角真值

因为俯仰角的定义域为[-90°90°],和反正弦的主值区间一致,因此可以直接求取真值。最后,将地面测量所得到的航向角作为常量直接加入到初始化中,就完成了应用低精度惯性测量单元在管道内检测中的初始对准。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




