捷联惯性导航技术优化方案

惯性导航定位的理论基础是牛顿定律，即在不受外力干扰情况下，运动的物体将一直保持匀速直线运动状态，外力对物体产生一个成比例的加速度。加速度可通过加速度计测得，对加速度进行时间的一阶和二阶积分可以得到速度和位置变化，在已知物体开始状态的位置、速度情况下，就可以通过测得的加速度计算得到对应时刻物体的位置信息。

1.捷联惯性导航算法的基本原理

在捷联惯性导航算法中，定位计算的加速度指运动物体在惯性空间的加速度，而实际加速度是在旋转的地球上测得的，受到地球旋转产生的向心加速度干扰，因此需要去除向心加速度引起的干扰，提取出物体在惯性坐标系内的加速度。该加速度相对于惯性空间内绝对静止参照物，绝对静止参照物指宇宙空间内无穷远处某一恒星。在地球表面的加速度测量值相当于是在一个运动的坐标系内测量一个相对静止坐标系内的矢量值，这时测得的加速度含有地球自转的角速度分量，称为哥氏加速度。将哥氏加速度转换为惯性加速度称为哥氏校正，即

式中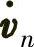，为n系下速度的变化率；f_b为加速度计测量值，通过转换矩阵C^b_n，将其变换为n系下测

量值；κ为由地球转动引起的无用角速度分量；g_n为n系下重力加速度测量矢量值。

哥氏校正涉及矢量的绝对变化率与相对变化率之间的关系，在微陀螺仪工作原理中的哥氏加速度也涉及这一问题。设一空间矢量a，其矢量值和方向都随时间而变化。过O点作一固定不动的观测坐标系Ox_iy_iz_i；过O点作一运动坐标系Oxyz。为了表示运动坐标系与固定坐标系的关系，设运动坐标系的单位矢量为e₁，e₂，e₃，由于Oxyz相对Ox_iy_iz_i运动，所以矢量a相对这两个坐标系的变化率是不相同的。矢量a在Oxyz中的变化率为（da/dt）_i，相对变化率为（da/dt）_r，由于只能取得运动坐标系下对矢量a的变化率观测值，如式（7-28）：

a=a_xe₁+a_ye₂+a_ze₃ （7-28）

设Oxyz相对固定坐标系Ox_iy_iz_i旋转的角速度为ω，则角速度用单位矢量表示为

ω=ω_xe₁+ω_ye₂+ω_ze₃ （7-29）

由于式（7-28）中a_x，a_y，a_z及e₁，e₂，e₃都随时间变化，所以矢量a的绝对变率为

（da/dt）i=d（a_xe₁+a_ye₂+a_ze₃）/dt

=（e₁da_x+e₂da_y+e₃da_z+a_xde₁+a_yde₂+a_zde₃）/dt （7-30）

式（7-30）中（e₁da_x+e₂da_y+e₃da_z）/dt项与运动坐标系的运动无关，只表示矢量a随动坐标系的变化率，称其为相对变率，表示为

（da/dt）r=（e₁da_x+e₂da_y+e₃da_z）/dt （7-31）

式（7-30）中（a_xde₁+a_yde₂+a_zde₃）/dt项与运动坐标系相对定坐标系转动的角速度ω有关，可以将三个矢量看作在定坐标系中转动的单位向径，因此可得

de₁/dt=ω×e₁

de₂/dt=ω×e₂

de₃/dt=ω×e₃ （7-32）

将式（7-32）代入式（7-30）中的后三项，得

（a_xde₁+a_yde₂+a_zde₃）/dt=a_xω×e₁+a_yω×e₂+a_zω×e₃=ω×a （7-33）

将式（7-33）和式（7-31）代入式（7-30）得

（da/dt）_i=（da/dt）_r+ω×a （7-34）

因此运动坐标系下的测量值可以通过式（7-34）转化为固定坐标系下的测量值，此时，如果测得的导数为加速度，则该加速度称为哥氏加速度，该校正公式称为哥氏校正。

利用n系下的速度矢量可求得采样时间PIG在n系的位移矢量d为

d=d₀+v_nt_s （7-35）

式中，d₀为前一采样时间的位移；t_s为采样时间。

通过捷联惯导计算可以求得PIG在n系的轨迹坐标，不需要利用外部定位手段实现对管道的地理坐标测量。利用陀螺仪跟踪加速度矢量的方向和陀螺仪测量机体坐标系相对于惯性坐标系的转动角度增量，推算得到转换矩阵。捷联惯导算法在每一次采样时间内需要更新三个，即姿态、速度和位置更新。姿态更新计算利用陀螺仪测量值改变姿态矩阵C^b_n。

2.余弦矩阵法表示姿态矩阵时间微分方程

捷联惯导算法的速度和位置计算见7.2.1节和7.2.2节捷联惯导定位的基本原理，本小节详细分析姿态计算方法。定义转换矩阵C^b_n为方向余弦矩阵，根据无限小转动矢量定理（即有限转动不是矢量，无限小转动是矢量），分析方向余弦矩阵随时间的变化问题，利用方向余弦矩阵的微分方程对这一问题进行描述。坐标系运动方式如图7-6所示，运动坐标系Ox_iy_iz_i相对固定坐标系Oxyz以角速度ω转动，运动坐标系内一点P用矢量r表示，运动坐标系相对固定坐标系的转换矩阵用C表示，C是ω的函数。r在运动坐标系与固定坐标系的投影关系为

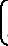xyzT=Cx_iy_iz_i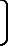^T （7-36）

P点的速度矢量可表示为

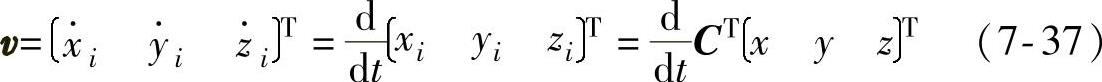
根据定理，将v=ω×r写成沿运动坐标系投影的矩阵形式：

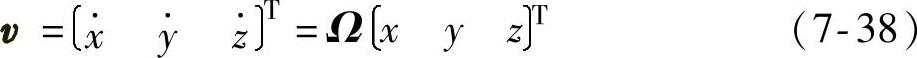
式中，Ω为ω变为矢量ω后在运动坐标系投影的反对称矩阵，即矢量与矢量叉乘的矩阵表达式：

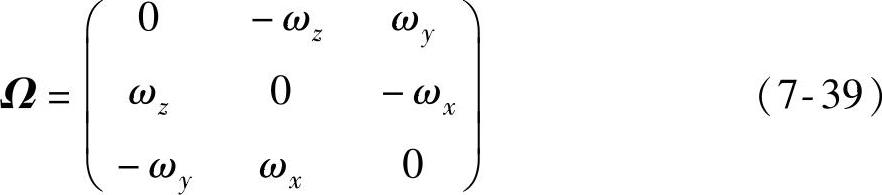
根据坐标转换公式（7-5），将式（7-38）左端写为

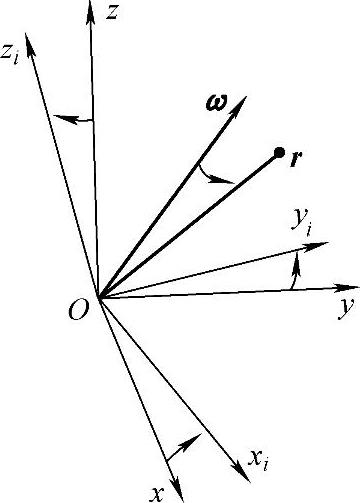
图7-6 坐标系运动方式

省略推导过程，经推导后得方向余弦矩阵微分方程为

已知初始条件，根据微分方程可以求得指定时间的姿态矩阵，但是计算过程中的计算误差和交换误差会使姿态矩阵失去正交性质，需要在计算后进行正交化，而余弦矩阵微分方程的正交化会带来正交误差，故利用四元数法解决这一问题。四元数法的正交化计算比方向余弦法简单，正交化误差不仅小于方向余弦法误差，也是目前所有姿态表达形式中最小的，所以在求解微分方程时采用四元数法作为姿态表达式。

3.利用四元数法表示姿态矩阵时间微分方程

四元数的计算思想可表述为：通过绕某一瞬时轴转过某个角度的一次转动获得绕定点转动的刚体角位置。四元数定义式为

Q=q+xi+yj+zk （7-42）

式中，q为实数基，其他三个基组成矢量基，关系为

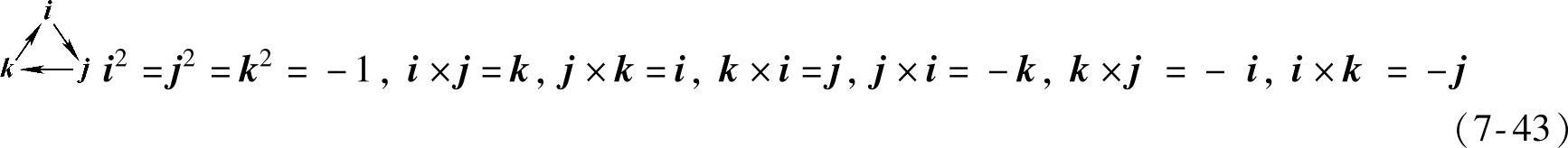
定义i、j、k为空间矢量基，四元数可重新定义为

Q=（q，q） （7-44）

式中，q为三维矢量；q为标量，当q²+x²+y²+z²=1时，Q为归一化四元数Q∗，则此时可以用三角函数表示为

Q^∗=cosθ+q^∗sinθ （7-45）

式中，q^∗为归一化后的单位矢量。因此，任意四元数都可以通过归一化与三角函数建立联系，归一化过程为

Q∗=Q（q²+x²+y²+z²）^-0.5 （7-46）

式中，（q²+x²+y²+z²）^-0.5为Q的模。

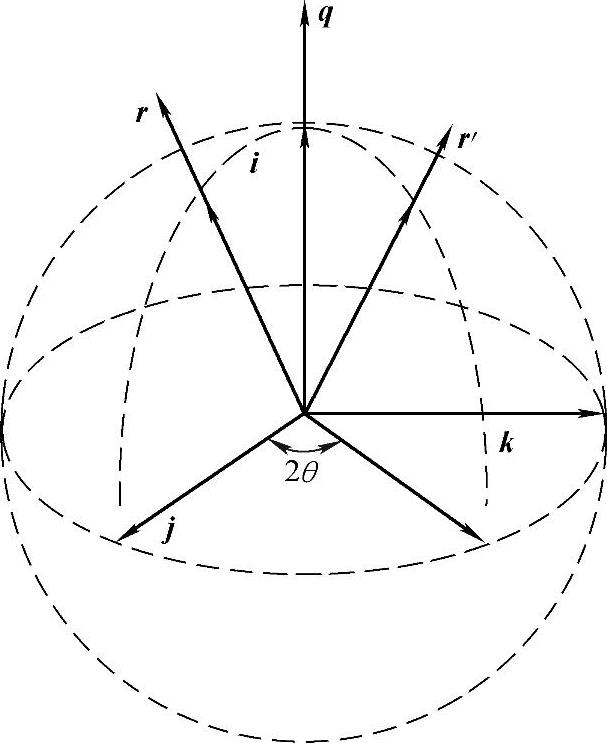
图7-7 四元数矢量转动

四元数的转动变换中，设有两个四元数Q和R，将它们分别归一化后用三角函数表示为

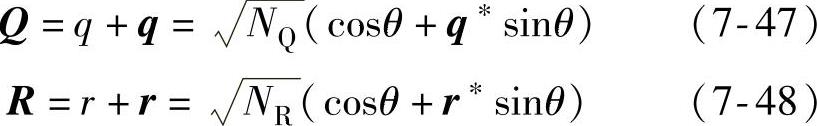
式中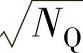，和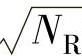分别为各自的模；q和r为各自的标量部分；q和r分别为矢量部分。

四元数矢量转动过程如图7-7所示，将R的矢量部分绕q方向沿锥面转2θ角可得一新四元数R′的矢量部分r′，且R′与R的模和标量部分都相等。

可得

R′=QRQ^-1=r₀′+r′ （7-49）

因此可以用单位四元数表示转动，即

Q=cos0.5θ+ζsin0.5θ （7-50）

式中，ζ为所绕的转动轴，图中的一次转动可将ζ看成q^∗。Q为转动四元数，由其对被转动的四元数施加转动算子Q（·）Q^-1，连续的转动可以表示为相继施加转动算子，但是这种转动的顺序不可交换。通过施加算子，可以使四元数绕ζ轴转动θ角度。利用四元数法进行姿态更新时，先用四元数法表示姿态矩阵，设固定坐标系为Oxyz，运动坐标系为Ox_iy_iz_i，设矢量M在固定坐标系的投影为

M=xi₁+yi₂+zi₃ （7-51）

M不动，运动坐标系相对固定坐标系绕q∗轴转过θ角，M在动系上的投影就相当于动系不动，M绕q∗轴转过-θ角得到的投影，因此有

x_ii₁+y_ii₂+z_ii₃=QRQ^-1=（q₀+q₁i₁+q₂i₂+q₃i₃）（xi₁+yi₂+zi₃）（q₀-q₁i₁-q₂i₂-q₃i₃） （7-52）

展开并按式（7-9）进行化简得

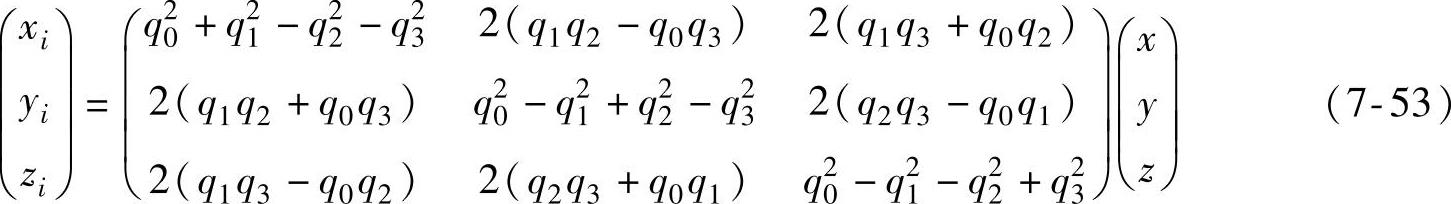
建立转动四元数的微分方程。设在t时刻运动坐标系相对固定坐标系转动的四元数表达为

R_i（t）=Q₁R（t）Q₁^-1 （7-54）

则在t+Δt时刻，由于运动坐标系的角速率ω而使两坐标系位置发生变化，此时运动坐标系相对固定坐标系的转动为Q₂转动，即

R_i（t+Δt）=Q₂R（t+Δt）Q₂^-1 （7-55）

则在t～t+Δt期间的运动坐标系的位置变化可(www.xing528.com)

用转动四元数Q₁^-1Q₂来表示，位置变化关系如图7-8所示。

运动坐标系的角速度ω与角增量的关系为

Δθ=│ω│Δt （7-56）

则用单位矢量表示t+Δt时刻的转动四元数为

Q₁^-1Q₂=cos（0.5│ω│Δt）+ζsin（0.5│ω│Δt） （7-57）

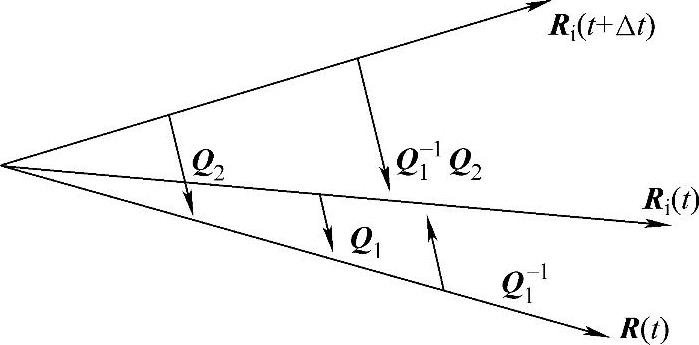
图7-8 四元数转动位置变化

通过其求解函数对时间的导数为

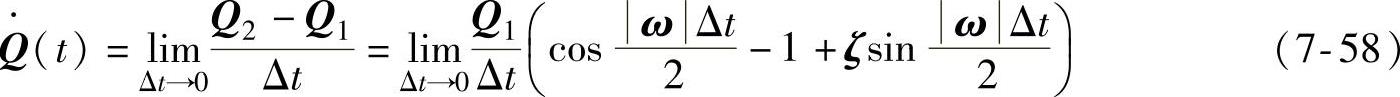
括号内的表达式可以利用泰勒级数展开为

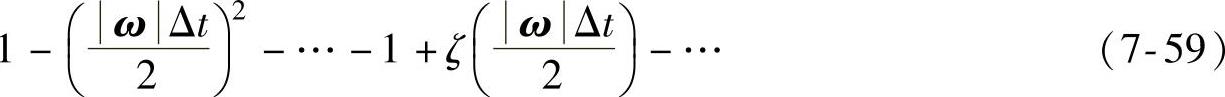
则经近似计算以后，可得四元数微分方程为

式中，ω为转动四元数，其只含有矢量部分。

式（7-60）为四元数法表示的姿态矩阵微分方程，比式（7-41）多了一个未知数，但是正交化计算比余弦矩阵法简单。余弦矩阵法需要使6个约束条件重新满足（这里不详细介绍），而四元数法只需进行一次最佳归一化，就可以实现计算结果的正交化。最佳归一化方法公式为

式中，Q为归一化以后的四元数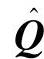；为归一化之前的四元数。

经归一化后，四元数表示的姿态矩阵符合正交性质，利用四元数表示姿态矩阵的微分方程。

4.更新算法的计算机数值解法

图7-1所示的捷联惯性导航算法需要三个更新过程，即姿态更新、速度更新和位置存储更新。对每个更新过程利用计算机进行求解，需要建立计算机执行算法。每个更新过程的计算机执行算法分别为：

（1）姿态更新算法 姿态更新算法是对四元数微分方程的求解过程。四元数法建立的姿态更新矩阵为

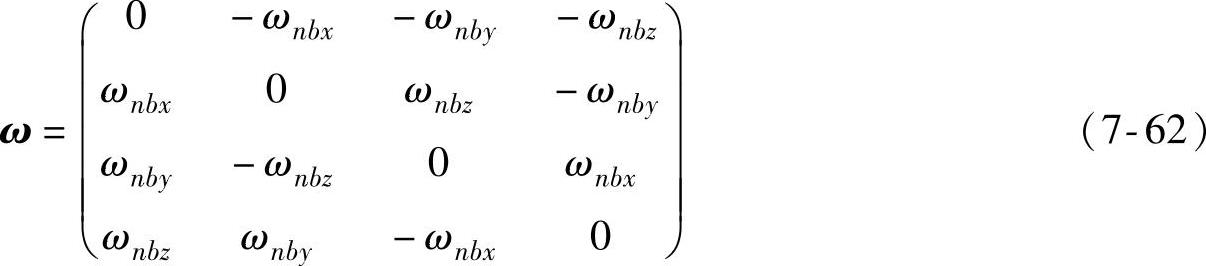
式中，x、y、z为b坐标系坐标轴方向；nb为n坐标系相对b坐标系的转动。

四元数微分方程式（7-60）的具体表达式为

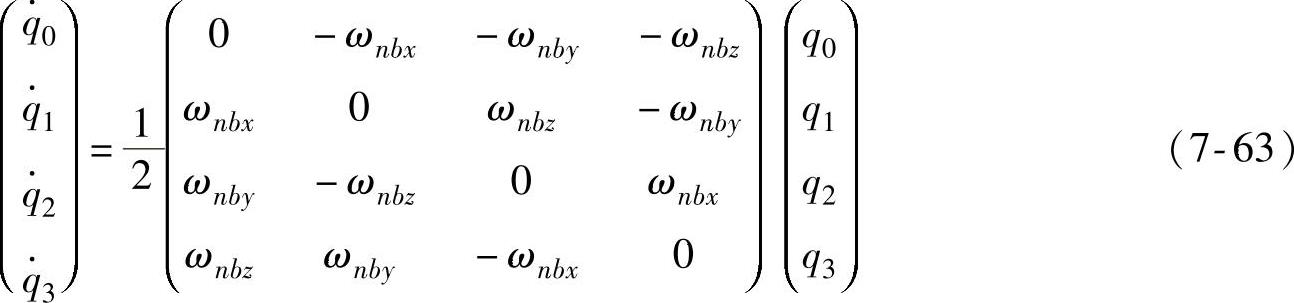
（2）速度更新算法 除了姿态更新，捷联惯性导航系统还需要速度和位置更新。PIG在n系下的速度投影可用三维矢量表示为

v_n=[v_nxv_nyv_nz]^T （7-64）

式中，v_nx为PIG速度在东向的映射值；v_ny为北向的映射值；v_nz为天向映射值。

由于加速度计传感器采用速度增量输出，每一采样周期的速度修正公式为

式中，v_nt为当前时刻的速度；v_n0为上一时刻速度；t为采样时间；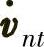

为当前时刻导航坐标系

下的加速度，通过哥氏校正式（7-35）得到。

一阶近似的微分方程为

式中，v_nt为当前时刻n系速度矢量；v_n0为前一采样时刻速度矢量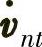；为速度增量，t_s为采样时间。

（3）位置更新算法 位置计算通过对每一步采样时间的位移求和得到，每步采样时间的位移根据速度积分得到，位置更新时间由加速度计的采样时间决定，PIG在每次采样周期内在n系内的位移为

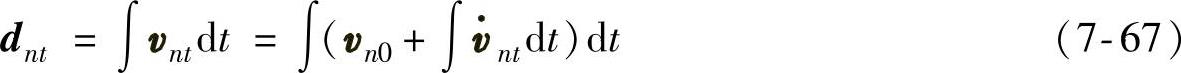
式中，d_nt为采样周期内PIG的位移。近似的位移计算微分方程为

式中，d_nt为当前时刻PIG在n系的位移。

由此可见，位移计算使用了姿态和速度计算的结果，因此姿态计算的精度需高于速度计算的精度，速度计算的精度高于位移计算的精度。

更新的计算机求解算法包括一阶欧拉法和四阶龙格库塔法。利用一阶欧拉法的求解算法为

y_i+1=y_i+hf（y_i），y′=f（y） （7-69）

一阶欧拉法的近似误差为C₁h。其中，C₁为一个常数项，h为计算的步长。四阶龙格库塔法计算的精度高于一阶欧拉法的计算精度，求解算法为

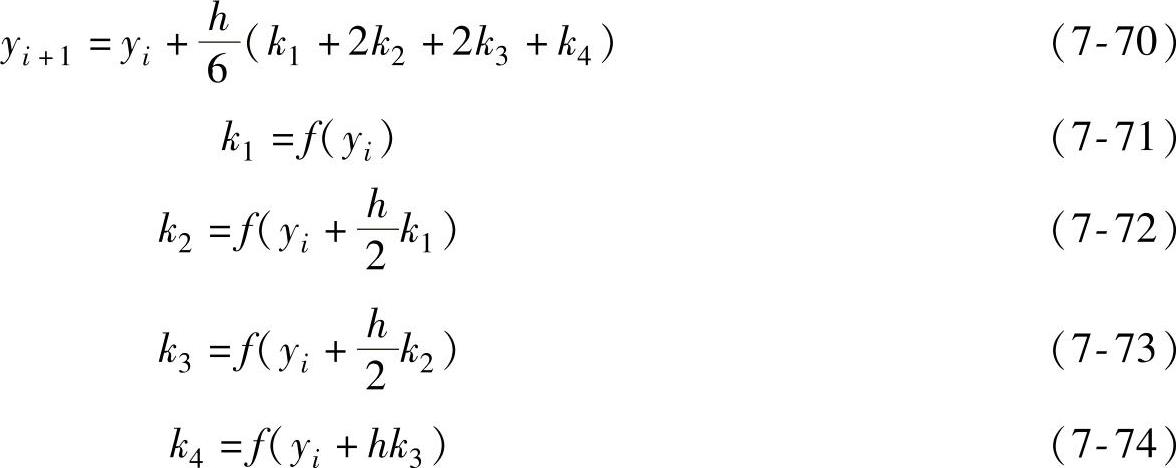
四阶龙格库塔法近似的误差为：C₂h。其中，C₂为一个常数项。四阶龙格库塔法计算量是一阶欧拉法的四倍，步长为其二分之一，而误差为其十六分之一。捷联惯性导航算法的姿态更新速度要高于速度更新和位置更新，且对姿态矩阵的精度要求更高。从花费的计算量与提高的精度两方面考虑，四阶龙格库塔法是一种综合性能最优的算法，所以选择其求解姿态更新矩阵，而用一阶欧拉法计算速度与位置更新。

在捷联惯性导航系统实际计算中，由于元器件测量误差、计算过程中数据的舍入误差及利用近似方法进行微分方程求解引入的近似误差等，造成定位精度受到限制，因此需要详细分析各种误差源和各种误差在捷联惯性导航算法中的传递方式，最终找出减少误差的方法。捷联惯性导航涉及的误差源主要包括初始对准误差、元器件测量误差和计算误差。

5.姿态角求解算法

姿态角可以根据式（7-8）求解，因为姿态矩阵符合正交性质，可得

则Cⁿ_b=（Cb_n）^-1，转换矩阵为正交阵，所以Cⁿ_b=（C_n^b）^T。得到姿态矩阵为

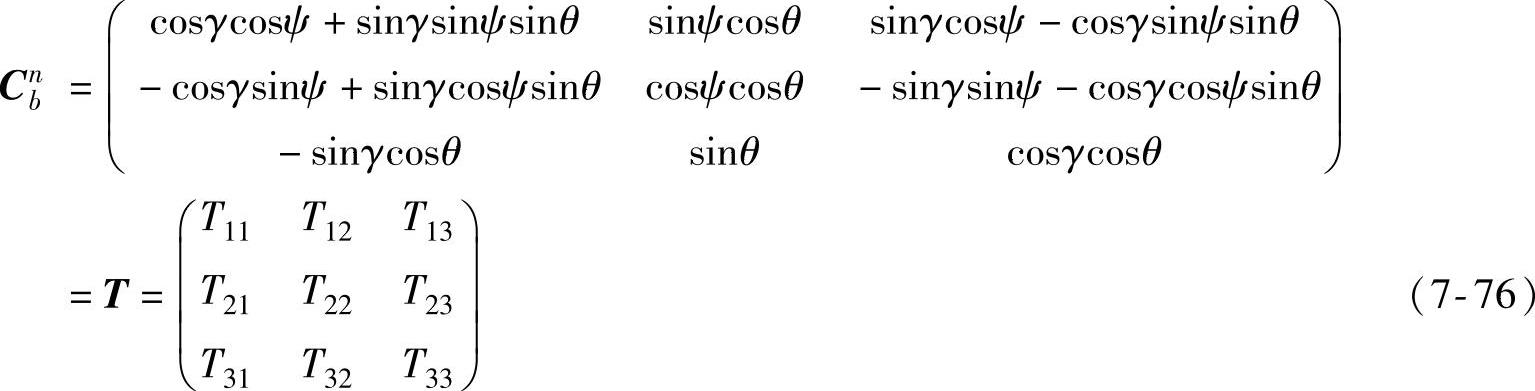
因为T是姿态角的函数，通过反三角函数可以得到姿态角，结果为

式中，下角标“主”表示通过矩阵元素计算得到的姿态角主值。

航向角的真值与主值范围如图7-9所示，可以看出，二者范围不同，对于其他两个姿态角也同样存在此问题。因此，需要将计算的主值转化为实际的真值，转换的方法见表7-2。

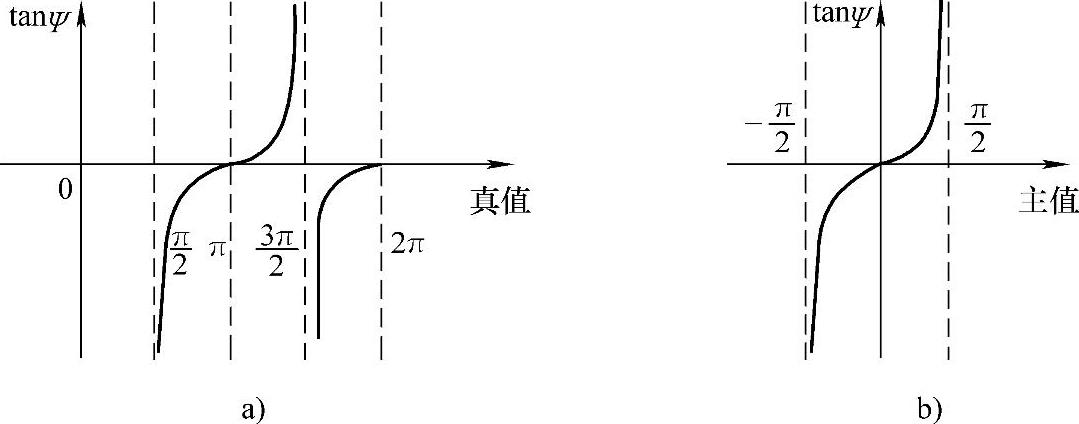
图7-9 航向角的真值与主值范围

a）真值范围 b）主值范围

表7-2 真值计算表

当俯仰角θ=90°时，其余弦值所在的矩阵元素会出现无穷小情况，因此数值计算不能利用式（7-77）求解，需要对横滚角与航向角的计算方法进行改进。

对姿态矩阵元素进行变换，即

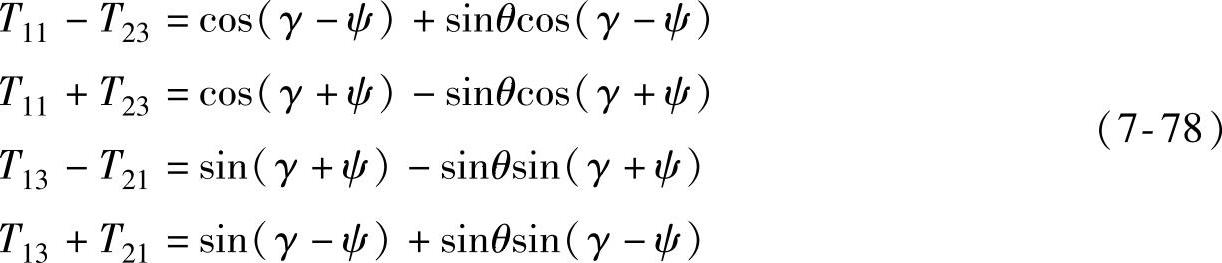
当θ=90°时，可得

T_11-T₂₃=2cos（γ-ψ）

T₁₃+T₂₁=2sin（γ-ψ） （7-79）

因此可求得

当θ=-90°时，可得

T₁₁+T₂₃=2cos（γ+ψ）

T₁₃-T₂₁=2sin（γ+ψ） （7-81）

因此可求得

这样姿态角计算的矩阵元素都为有界值，避免计算式中出现cos90°情况。