参考坐标系及转换方法简介

在参考坐标系内研究管道内检测器（搭载有检测器的管道清管器，简称PIG）的运动和位置变化。参考坐标系包括导航坐标系、地理坐标系和载体坐标系。导航坐标系用n表示，载体坐标系用b表示，地理坐标系用t表示，惯性坐标系用i表示。地理坐标系用来表示管道的位置，设计时将PIG运动的导航坐标系看作地理坐标系。各坐标系定义见表7-1。

表7-1 坐标系定义

所有坐标系均采用正交的笛卡儿坐标系，坐标系各轴正向顺时针转动为正，如图7-3箭头所示。规定每个坐标轴的旋转正方向都与图7-3b中z轴箭头方向一致。根据b系和n系之间的相对转动关系，可以求得PIG的姿态角。姿态角表示PIG转动过程中的姿态信息，包括航向角、俯仰角和横滚角，分别用ψ、θ和γ表示。b系中旋转z轴，y轴在水平面的投影与n系y轴的夹角，即PIG前进方向与地理坐标北向夹角为航向角，数值以北向为起点，顺时针方向计算，范围为0°～360°。b系中旋转x轴，x轴与y轴确定的平面与n系水平面的夹角为俯仰角，以水平面为起点，仍是顺时针旋转为正，范围为0°～360°。b系中旋转y轴，y轴和z轴平面与n系天向和北向垂直面的夹角为横滚角，y轴顺时针为正，范围为0°～360°。

在一种参考坐标系下得到载体的测量值，现保持载体不变，改变参考坐标系，在另一种坐标系下得到同一载体的测量值，这种方法称为坐标转换。现在分析坐标转换问题，如图7-4所示，在坐标系x₀y₀z₀中观察一定点P，坐标为（x₀，y₀，z₀），旋转坐标系到x_ry_rz_r，在新的坐标系中求P点的坐标。

可以通过三次转动从坐标系x₀y₀z₀变换到x_ry_rz_r。转动方法为：第一次先旋转z₀轴，使x₀y₀平面内的直角坐标系x₀y₀旋转一个ψ角，得到新的坐标系x_ay_az_a；第二次旋转x_a轴，使z_ay_a平面内的坐标系旋转θ角，得到坐标系x_ry_rz_r；第三次旋转y_r轴，使x_rz_r平面内的坐标系旋转γ角。通过三次转动最终完成坐标转换，每次转动P点的坐标都会发生变化，以第一次转动为例，P点的z坐标不变，x、y的坐标变化根据余弦函数法求解。设P点在xy平面的投影为F，如图7-5所示。

图7-3 坐标系转动方向

a）三维立体视图 b）z轴俯视图

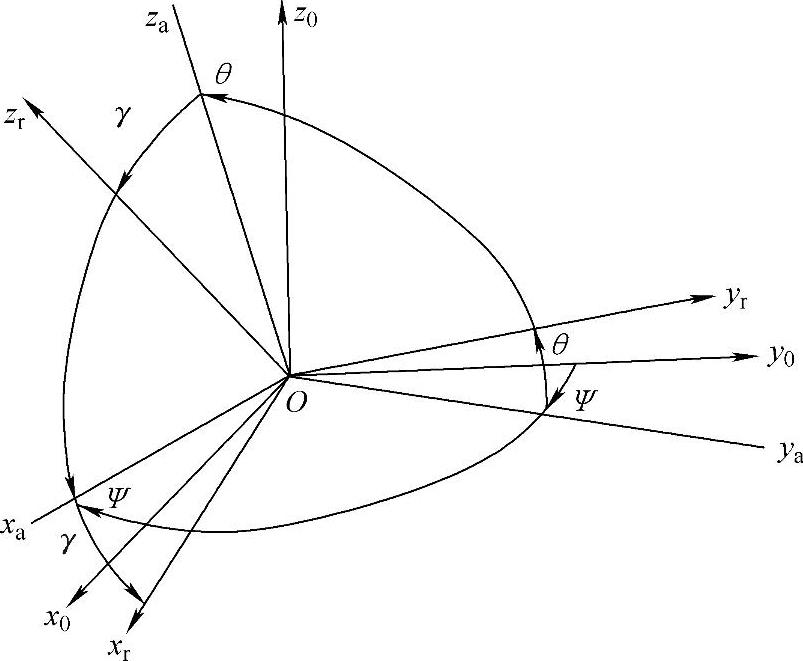
图7-4 坐标转换示意图

图7-5 P点在xy平面的投影

设测量点位置为F，在原始坐标系下为（x₀，y₀），x₀=OH=BF，y₀=OB=HF，将坐标系以原点为轴向右转ψ角度，F点在新坐标系下为（x_a，y_a），x_a=OD=GF，y_a=OG=DF，过点B和H向两坐标轴分别作垂线。当右转为正时，新坐标系下观测位置与原始位置关系为

OD=OE-DE=OHcosψ-HFsinψ （7-1）

OG=OA+AG=OBcosψ+BFsinψ （7-2）

所以有

x_a=x₀cosψ-y₀sinψ （7-3）

y_a=x₀sinψ+y₀cosψ （7-4）

三维坐标系下将方程用矩阵形式表达为

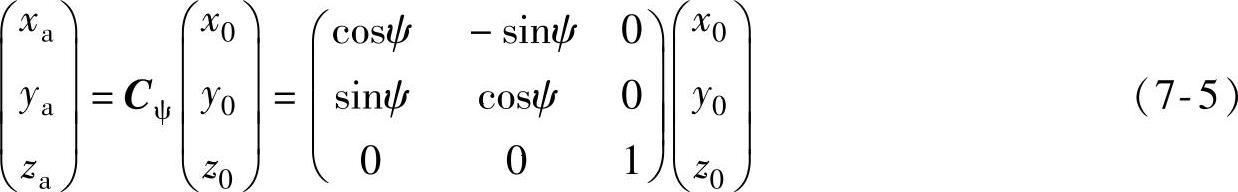
式中，C_ψ为转换矩阵，利用其左乘坐标矢量就得到旋转坐标系下的位置。

按这样的转换方法，规定不改变转动先后次序，将向右旋转（如第一次旋转方向，从z轴反向看xy平面，顺时针旋转）设为正，则可得从x₀y₀z₀到x_ry_rz_r坐标系的转换矩阵C^b_n为

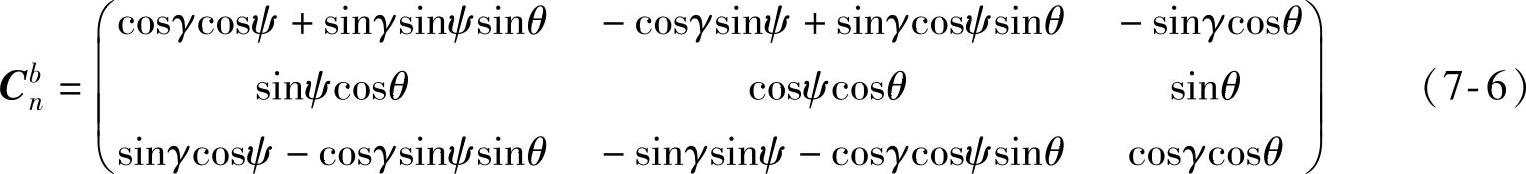
C^b_n为依次左乘转换矩阵，即

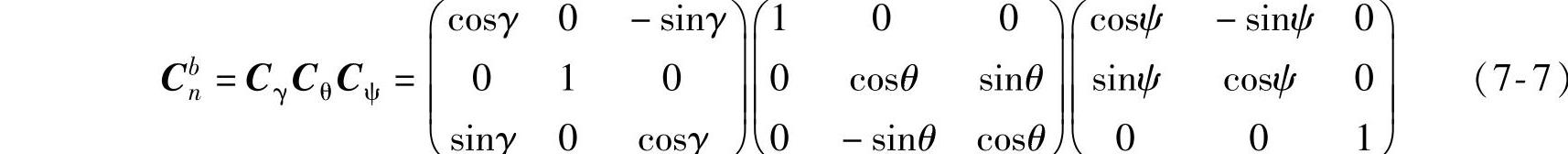
式中，C_θ为旋转x_a轴的转换矩阵；C_γ为旋转y_r轴的转换矩阵。

Cb_n必须为正交矩阵，即

C^b_nCⁿb=C^b_n（C^b_n）T=I （7-8）

如果已知某一时刻的姿态矩阵，可以直接通过式（7-9）进行转换：

Xⁿ=Cⁿ_bX^b （7-9）(www.xing528.com)

式中，X为三维矢量；Xⁿ为在n系下的测量值；X^b为在b系下的测量值。

如此，就得到了在三维坐标系下，将b系测量值转换到n系中的计算方法。

姿态矩阵具有正交性质。设直角坐标系Ox_iy_iz_i的单位矢量为i₁，i₂，i₃，则三者应互相垂直，且模为1；另一直角坐标系Oxyz的单位矢量为e₁，e₂，e₃，同样三者互相垂直，模为1。通过矩阵C将坐标系Ox_iy_iz_i转换到坐标系Oxyz，即

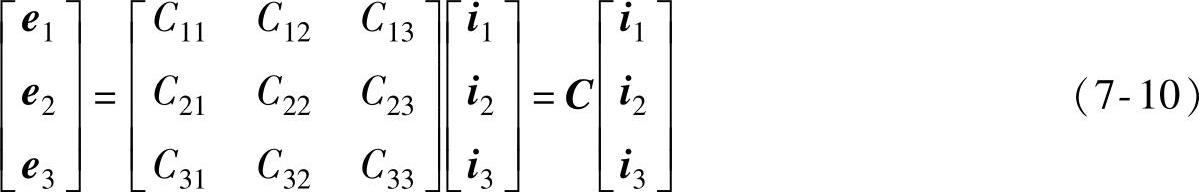
将式（7-10）中的矩阵换算为方程组，即

e₁=C₁₁i₁+C₁₂i₂+C₁₃i₃ （7-11）

e₂=C₂₁i₁+C₂₂i₂+C₂₃i₃ （7-12）

e₃=C₃₁i₁+C₃₂i₂+C₃₃i₃ （7-13）

因为e₁，e₂，e₃为互相垂直的单位矢量，所以可得

e₁×e₂=e₃ （7-14）

e₂×e₃=e₁ （7-15）

e₃×e₁=e₂ （7-16）

将式（7-11）～式（7-13）代入式（7-14）～式（7-16）可得

对矢量进行运算。因为单位矢量对应系数相等，可得

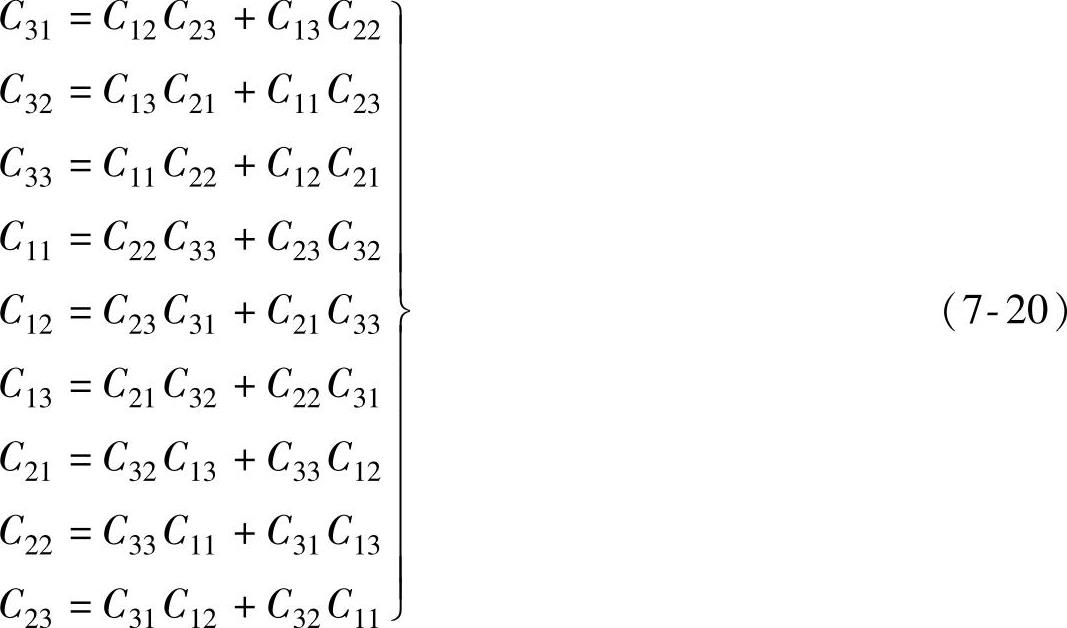
方程组式（7-20）说明，矩阵C的任一矩阵元素都等于其代数余子式。同理，对于矢量e₁，e₂，e₃应有

e₁·e₁=e₂·e₂=e₃·e₃=1，e₁·e₂=e₂·e₃=e₃·e₁=0 （7-21）

将式（7-11）～式（7-13）代入式（7-21）可得

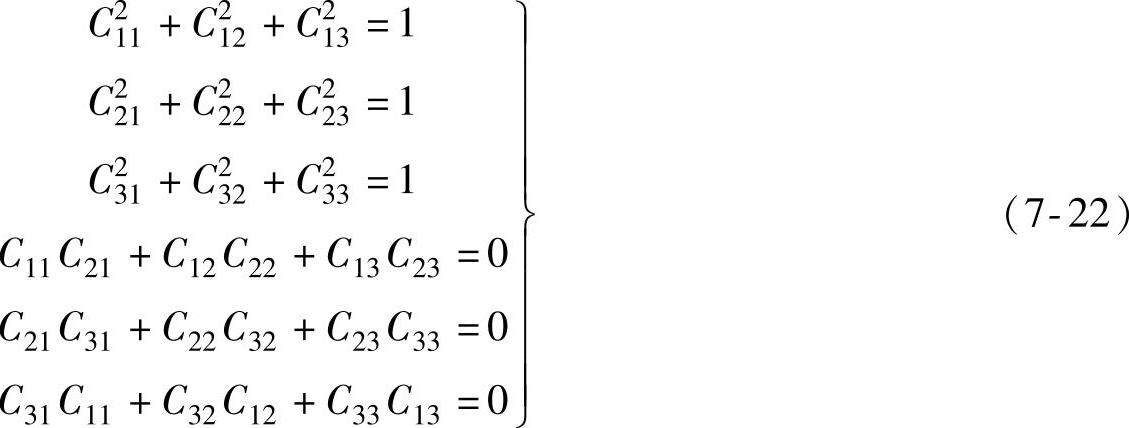
由方程组式（7-20）和方程组式（7-22）可得C的行列式为1，并可得

式中，M₁₁，M₁₂，M₁₃为C₁₁，C₁₂，C₁₃的代数余子式，同时可得

detC=C²₁₁+C²₁₂+C²₁₃=1 （7-24）

根据矩阵求逆公式，有

式中，C^∗为C的伴随矩阵。

根据式（7-23）和式（7-24）得

式中，C^T为C的转置矩阵，因此姿态矩阵C为正交矩阵。