式中，Mij[ξj（t）]为ξj（t）对于Mij的隶属度，并且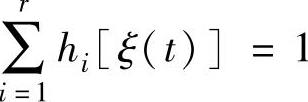
。
采用平行分布补偿控制策略，则模糊状态反馈控制律为
式中，Ai、Bi分别为适当维数的矩阵；x（t）∈Rn，为状态矢量；u（t）∈Rm，为输入矢量；i=1，2，…，r为模糊规则的数量；Ri为该模糊系统第i条规则。
采用单点模糊化、乘积推理规则及中心加权清晰化，式（6-33）可以写为
式中，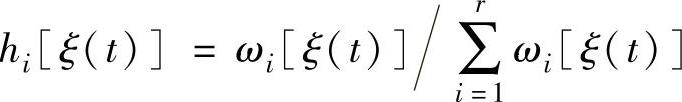
。
式中，Mij[ξj（t）]为ξj（t）对于Mij的隶属度，并且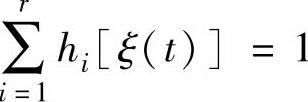
。
采用平行分布补偿控制策略，则模糊状态反馈控制律为
鉴于：
鉴于：
将模糊状态反馈控制律，即式（6-36）的后件带入基于T-S模糊模型的非线性被控对象，即式（6-34）中，则闭环控制系统可以重建为
将模糊状态反馈控制律，即式（6-36）的后件带入基于T-S模糊模型的非线性被控对象，即式（6-34）中，则闭环控制系统可以重建为
此T-S模糊模型的闭环稳定性可由Lyapunov稳定性理论得出，具体分析如下：
首先选择一个二次型非负能量函数作为Lyapunov函数，即
V（t）=xT（t）Px（t） （6-39）
注意到对于任意合适维数的列矢量x（t）、y（t）和一个对称方阵Q=QT，有如下事实：
xT（t）Qy（t）=yT（t）Qx（t） （6-40）
则沿着闭环系统方程求V（t）的时间导数，可得
此T-S模糊模型的闭环稳定性可由Lyapunov稳定性理论得出，具体分析如下：
首先选择一个二次型非负能量函数作为Lyapunov函数，即
V（t）=xT（t）Px（t） （6-39）
注意到对于任意合适维数的列矢量x（t）、y（t）和一个对称方阵Q=QT，有如下事实：
xT（t）Qy（t）=yT（t）Qx（t） （6-40）
则沿着闭环系统方程求V（t）的时间导数，可得
容易看出使得闭环模糊系统稳定的条件，也就是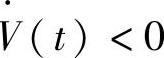
的条件是存在下面的负定矩阵：(www.xing528.com)
[P（Ai+BiKj）+（Ai+BiKj）TP]＜0 （6-42）
即使得：
PAi+ATiP+PBiKj+KjTBiP＜0 （6-43）
由于式中Kj和P均为待求变量，因此这是个非线性矩阵不等式。
下面将其转化为可以利用Matlab鲁棒控制LMI（linear matrix inequalities）工具箱求解的线性矩阵不等式。
令X=P-1，并与上面的非线性矩阵不等式进行左乘和右乘，故得
AiX+XATi+BiKjX+XKjTBTi＜0 （6-44）
再令Yj=KjX，式（6-44）可进一步转化为
AiX+XATi+BiYj+YjTBTi＜0 （6-45）
式（6-45）的待求变量X和Yj，j=1，2，…，r可通过LMI工具箱求得可行解。
最终使得闭环T-S模糊系统稳定的状态反馈控制器增益可通过式（6-46）计算得出：
Kj=YjX-1（j=1，2，…，r） （6-46）
容易看出使得闭环模糊系统稳定的条件，也就是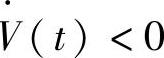
的条件是存在下面的负定矩阵：
[P（Ai+BiKj）+（Ai+BiKj）TP]＜0 （6-42）
即使得：
PAi+ATiP+PBiKj+KjTBiP＜0 （6-43）
由于式中Kj和P均为待求变量，因此这是个非线性矩阵不等式。
下面将其转化为可以利用Matlab鲁棒控制LMI（linear matrix inequalities）工具箱求解的线性矩阵不等式。
令X=P-1，并与上面的非线性矩阵不等式进行左乘和右乘，故得
AiX+XATi+BiKjX+XKjTBTi＜0 （6-44）
再令Yj=KjX，式（6-44）可进一步转化为
AiX+XATi+BiYj+YjTBTi＜0 （6-45）
式（6-45）的待求变量X和Yj，j=1，2，…，r可通过LMI工具箱求得可行解。
最终使得闭环T-S模糊系统稳定的状态反馈控制器增益可通过式（6-46）计算得出：
Kj=YjX-1（j=1，2，…，r） （6-46）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
