水平直管道加速度控制系统模型分析

内检测器处于水平管道中时，重力完全成为对管道的压力，如图6-3所示。由滑动摩擦力公式可以推导出由于重力所引起的阻力。

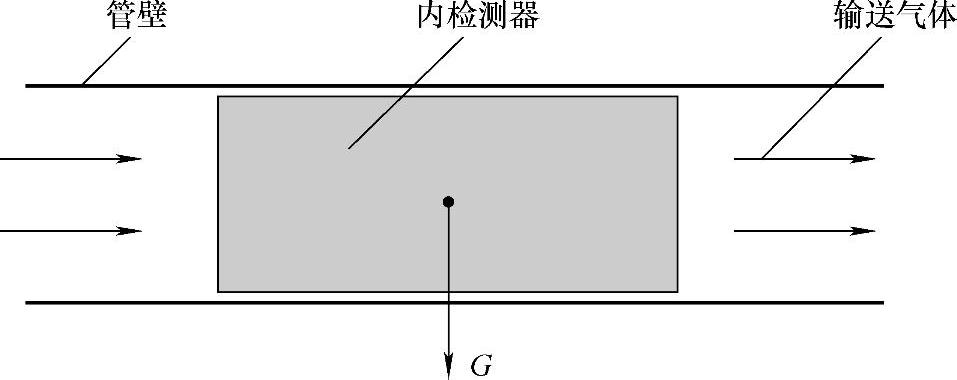
图6-3 水平管道中的内检测器

由于内检测器是在前后端压力差的作用下运行的，运用动力学理论即牛顿第二定理，得到描述内检测器在水平管道流场中行走的动力学方程为

ma（t）=F_P-（mg+F_μ）μ-F_W （6-1）

式中，m为内检测器质量；a（t）为内检测器水平加速度；F_P为内检测器两端的压力差；g为重力加速度；F_μ为永磁体对管壁的吸附力；μ为磁阻系数；F_W为内检测器上的皮碗等元件与管壁产生的摩擦阻力。

F_W可分为静摩擦阻力和动摩擦阻力两种，与式（6-1）的其他项相比较，无论是哪一种，其数值都很小，可以忽略不计。因此式（6-1）可改写为

ma（t）=F_P-（mg+F_μ）μ （6-2）

式中，内检测器两端的压力差F_P包含静压力差与动压力差，即

F_P=F_S+F_D （6-3）

式中，F_S为静压力差，表达式为

F_S=ρ₁gV₁-ρ₂gV₂（ 6-4）

式中，ρ₁为内检测器上游的气体密度；V₁为上游的气体体积；ρ₂为内检测器下游的气体密度；V₂为下游的气体体积。

气体密度可通过内检测器两端的密度计测出，上游的气体体积可通过管道横截面面积与长度乘积得到，即

F_S=ρ₁gSl-ρ₂gS（L-l） （6-5）

式中，S为管道横截面面积；L为管道总长；l为内检测器途径路径的长度。(www.xing528.com)

式（6-3）中，F_D为动压力差，表达式为

式中，ρ₁为内检测器上游的气体密度；v为上游的气体流速，其数值可通过气体体积与管道横截面积之商求出，即

式中，R为管道内半径；r（t）为内检测器的泄流孔半径。

综合式（6-2）、式（6-5）及式（6-7）可得

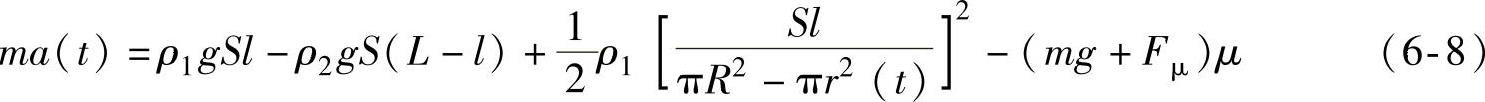
经过整理，可得

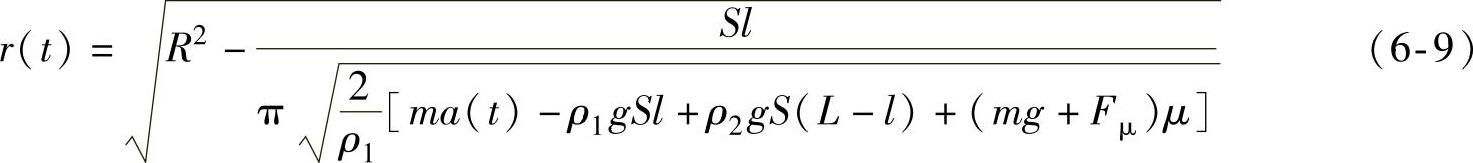
由式（6-9）可知，内检测器泄流孔半径与加速度值之间为单调递减函数，由此可知泄流孔半径越大，内检测器的加速度值越小。

式（6-9）中的参数由以下方法确定：m为内检测器质量，可以通过称重设备测量得到；R为管道内半径，S为管道横截面积，L为管道总长，可以根据管道的建设标准来确定；ρ₁和ρ₂为内检测器上、下游的气体密度，可根据安装在内检测器前后两端的密度计测得；（mg+F_μ）μ为由重力以及永磁体对管道壁的吸附力形成的阻力数值，可利用绞盘牵引内检测器的方法获得；l为内检测器途径路径的长度，可利用算法与加速度计输出联合求出。

倾角器实时记录内检测器前进方向与重力方向的夹角。在水平管道中，倾角器数值为90°。如果将倾角作为速度控制的输入参数，则式（6-9）可修改为

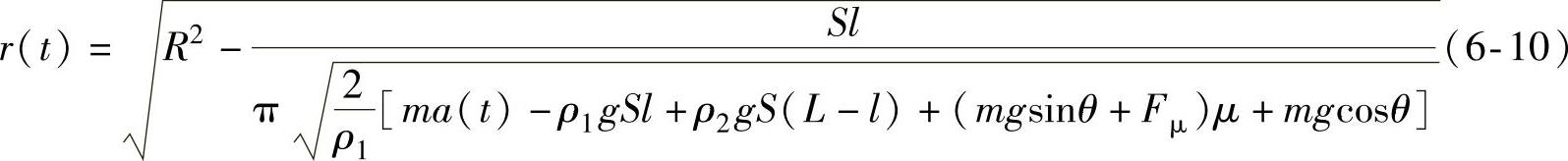
式中，θ为检测器前进方向与重力方向的夹角，且θ=90°。