复合材料的可靠性优化设计

在复合材料层合板重量一定的约束条件下，以系统的可靠度指标最大为目标，对纤维铺设角及单层板的相对厚度进行优化设计，则可靠性优化问题表示为

式中：x为设计变量，可以是单变量，也可以是多变量；f（x）为目标函数；W为结构重量。

复合材料的可靠性分析和可靠性设计是一个非常复杂的问题。在寻优过程中，涉及大量的矩阵运算和近似求解。遗传算法（genetic algorithm，GA）是人们通过模拟生物进化过程发展出的一种算法，具有简单通用、不需要求导、可进行全局优化搜索、适于并行处理以及应用范围广等特点，能够有效地克服可靠性优化设计中的困难。

粒子群优化算法（particle swarm optimization，PSO）源于对鸟类捕食行为的模拟，是另一种全局优化进化算法。以下结合PSO讨论复合材料的可靠性优化设计。假设有一个四边简支对称复合材料层合板（见图10-38），受x、y两个方向压缩载荷Nx、Ny及横向均布载荷p 0作用，板的尺寸为a×b。对层合板结构进行分析，得到控制微分方程为

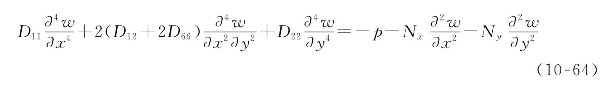
图10-38　层合板受载情况

对方程求解可得层合板的挠度为

第k个单层板内的应力为(www.xing528.com)

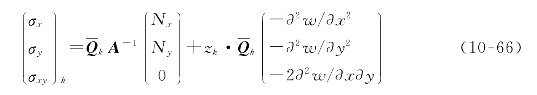
式中：为第k个单层板的变换刚度矩阵；zk为层合板中第k个单层板中面的z方向坐标。

在实际工程问题中，单层板的铺设角一般是按照某些特定角度给出的。假定可供选取的铺设角为-45°、0°、45°、90°。采用单层板铺设角的指标变量x=-1、0、1、2分别表示角度为-45°、0°、45°、90°的复合材料单层板。在总厚度一定的情况下，通过优化各单层板铺设角（顺序），使结构的系统可靠度最大。若层合板含有10个单层板，则其优化模型可以描述为

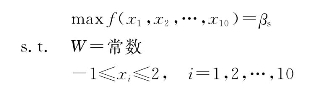
式中：xi为第i个单层板铺设角的指标变量，其值为整数变量；W为层合板重量或厚度。

考虑铺层结构为（x1/x2/…/x10）s、单层板厚度为0.1 mm、总厚度为2 mm的对称层合板。Nx=3.0×105 N/m，Ny=kNx，p0=0.8×105 Pa。弹性常数为E1=181.0 GPa，E 2=10.7 GPa，G12=7.17 GPa，μ=0.28。强度参数的统计特性如表10-11所示。

表10-11　强度参数统计特征

采用Tasi-Wu失效准则和一次二阶矩方法分析层合板的可靠度，然后用改进粒子群算法对层合结构进行可靠性优化设计，计算结果见表10-12。可以看出，系统的可靠度随着载荷的增加（k的增加）逐步减小。当载荷一定（k=0.2和k=0.4）时，在达到优化目标（系统可靠度指标最大）的前提下，分别得到两组不同的优化解。

表10-12　优化结果