基于有限元数值分析的层合板强度预测技术

以下利用有限元计算软件ANSYS对层合板的初始强度及最终强度进行预测。分析时采用SOLID单元，破坏准则利用三维Tsai-Wu准则［4］，即

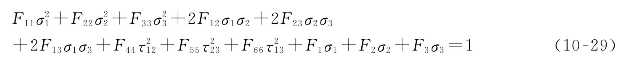
式中：各系数分别为

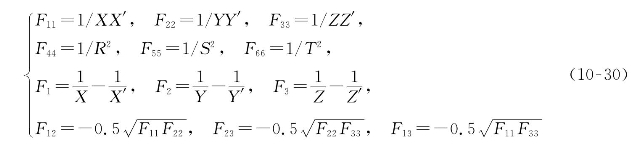
式中：X、X＇分别为纤维方向的拉、压强度；Y、Y＇分别为横方向的拉、压强度；Z、Z＇分别为厚度方向的拉、压强度；R和T为纵向剪切强度；S为横向剪切强度。各强度参量的值分别取为［8］

当某一单层满足式（10-29）所示的破坏条件时，认为该层刚度消失（刚度值为零），然后继续加载，预测下一个破坏的单层，直至所有单层均发生破坏，由此确定最终强度。计算结果见表10-9、表10-10和图10-25。

表10-9　A类板最终强度预测值与试验值的比较(https://www.xing528.com)

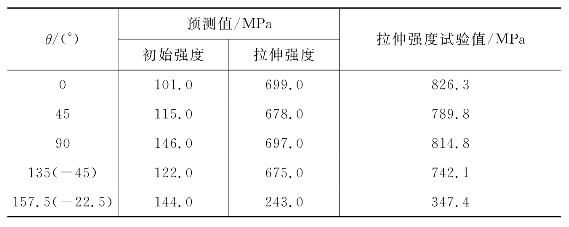
表10-10　B类板最终强度预测值与试验值的比较

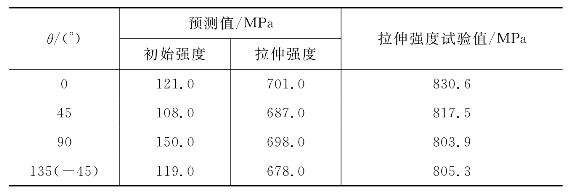
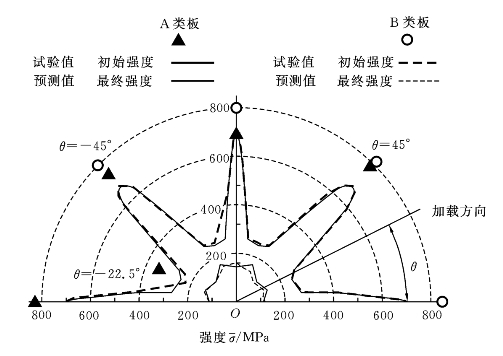
图10-25　强度与加载方向的关系

与经典层合板理论不同，有限元数值方法考虑了面外应力分量的影响，以及边缘效应，各单层内的应力不再是均匀的。某个单元最先满足Tsai-Wu准则，则认为该单元所在的单层发生破坏。

在计算时，只要某单层满足强度准则，则认为该层刚度消失，但实际上材料还可继续承担一部分载荷。因此，计算结果偏于保守，计算的强度值小于试验值。从表10-9、表10-10中可以看出，加载方向对强度的影响较大。不论A类板还是B类板，0°层在表层时，板的强度都较大。当板内不含0°以及90°层时，初始破坏强度上升，而最终强度大大降低。最终强度的计算值基本上反映了加载方向对强度的影响规律，但复合材料层合板的损伤形态与强度机理十分复杂，对最终强度的精确预测不是一件容易的事，还有待进一步的研究。

结合试验和有限元数值方法对层合板的强度进行分析，在一定范围内揭示不同层合结构（或不同加载方向）内部的损伤扩展规律和强度特征，可以为层合板结构的强度预测方法的建立，以及复合材料的优化设计提供依据和参考。