强度准则的重要性和应用

当单层板处于面内任意应力状态时，通过坐标变换，可求出材料主轴方向的应力σ1（σL）、σ2（σT）和τ12（τLT），如图10-5所示。判定单层板发生破坏的最大应力准则表示为

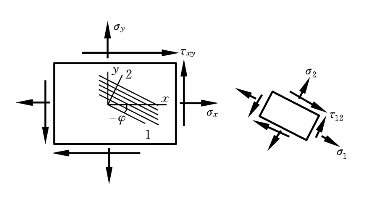
图10-5　面内受力单元体

根据σ1的正、负号，σ1u=Xt或Xc；根据σ2的正、负号，σ2u=Yt或Yc；τ12u=S。式（10-9）中，若有任一不等式成立，则表明单层板发生破坏。

σ1、σ2和τ12与试样整体坐标系下的应力分量σx、σy和τxy之间存在下面的关系：

式中：T为坐标变换矩阵，即

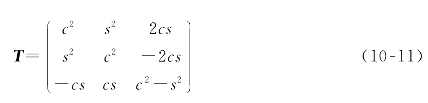
式中：　

在单向拉伸应力状态（偏轴拉伸）下，σy=0，τxy=0，有：σ1=c 2σx，σ2=s2σx，τ12=-csσx。根据式（10-9），得到引起单层板破坏的σx的临界值如下：

由式（10-12）确定的三个临界值中，最小的一个临界值即为单层板发生破坏的临界值。

由式（10-12）预测的偏轴拉伸断裂强度如图10-6所示。沿纤维方向的断裂只有当φ非常小时才发生，随着偏角φ的增大，断裂形式转为剪切断裂和横向（基体）断裂。

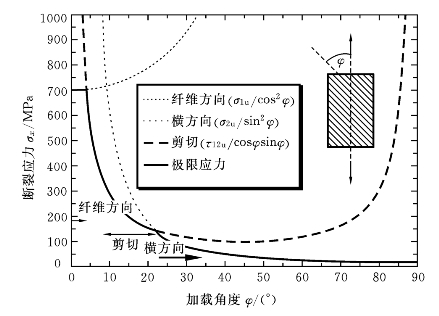
图10-6　玻璃纤维/聚乙烯复合材料断裂应力与φ的关系

考虑材料中的各向异性，将金属的屈服条件加以扩展，得到下面的Tsai-Hill准则，即

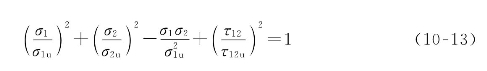
当σ1为拉应力时，σ1u=Xt；反之，σ1u=Xc。同样：当σ2为拉应力时，σ2u=Yt；当σ2为压应力时，σ2u=Yc。根据式（10-13），在偏轴拉伸条件下，求得破坏的临界应力为

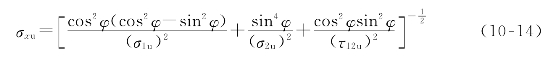
在Tsai-Hill准则中，对具体的断裂模式并不加以区分。图10-7所示为最大应力准则和Tsai-Hill准则下碳纤维/环氧树脂复合材料单层板偏轴拉伸强度实测值与理论值的对应关系。一般情况下，基于Tsai-Hill准则可获得更高的预测精度。定义(www.xing528.com)

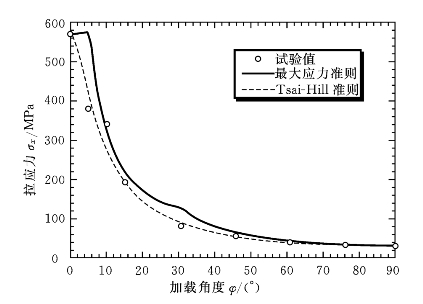
图10-7　碳纤维/环氧树脂复合材料单层板偏轴拉伸强度实测值与理论值

式中：F.I.为“failure index”（破坏指标）的缩写。

F.I.=1表示材料处于破坏的临界状态，F.I.＜1表示尚未发生破坏，F.I.＞1表示已发生破坏。F.I.＜1时，这个值距离1越近，说明材料越接近破坏。由Tsai-Hill准则只能判定材料是否发生破坏，而不能判定发生了何种形式的破坏。由于考虑了应力分量的相互影响，由最大应力准则判定不会发生破坏的情形，可能会满足Tsai-Hill破坏条件。

还有一种强度的张量理论，称为Tsai-Wu理论。该理论也不区分具体的断裂模式，其表达式为

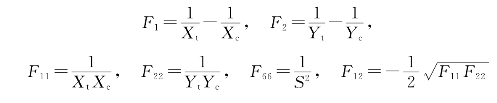
式中：Xt、Xc分别为沿纤维方向的拉伸和压缩强度；Yt、Yc分别为横方向拉伸和压缩强度；S为Oxy面内的剪切强度。

Tsai-Wu理论是应用较为广泛的一种理论。

例10-1　一碳纤维/环氧树脂复合材料单层板受面内载荷作用，如图10-8所示。利用Tsai-Hill准则判断该板是否发生破坏，如果发生破坏，会是什么破坏。已知：E1=140 GPa，E2=10 GPa，G12=5 GPa，μ12=0.3，Xt=1 500 MPa，Xc=1200 MPa，Yt=50 MPa，Yc=250 MPa，S=70 MPa。

解　首先求出材料主轴方向的应力分量。因θ=45°，m2=n2=mn=0.5，根据应力的坐标变换关系，有

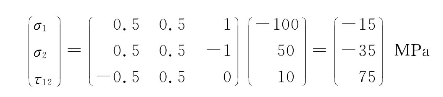
图10-8　单层板受面内加载作用（单位：MPa）

由Tsai-Hill准则，得到破坏指标为

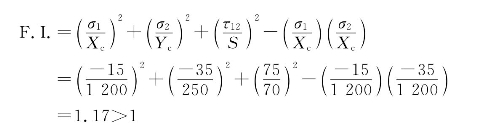
所以，该板将发生破坏。为判断破坏模式，需要进一步由最大应力准则计算各个方向对应的破坏指标。计算结果如下：

因此，破坏模式为面内剪切破坏。