正交各向异性材料的应力应变关系优化

纤维沿同一方向整齐排列的单向复合材料具有非均匀性和各向异性。但在考虑单向复合材料的整体力学行为时，把包含纤维和基体的适当大小的体积单元看作材料的基本构成元素，材料中各处元素的性质相同，因此图10-1（a）所示的材料从宏观上看可以认为是均质材料。该材料有两个正交的对称平面，即1-3面和2-3面。该材料称为正交各向异性材料（orthotropic materials）。1、2、3轴（或L、T、Z轴）称为材料主轴，其中1（L，longitudinal）表示纤维方向，2（T，transverse）表示与纤维相垂直的方向。

在平面应力状态假设下，沿材料主轴方向的应力和应变之间存在下面的关系（本构方程）：

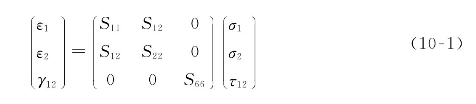
式中：Sij称为柔度系数（compliance coefficient），它们与工程弹性常数之间的关系是

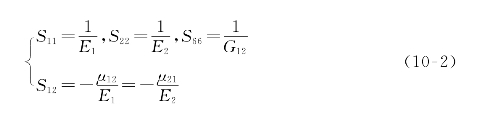
对式（10-1）求逆，得到下面的由应变求应力的公式：

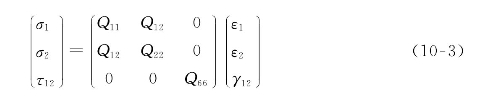
式中：Qij称为折减刚度（reduced stiffness）系数，各折减刚度系数与工程弹性常数之间的关系为

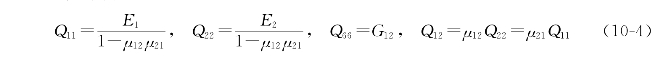
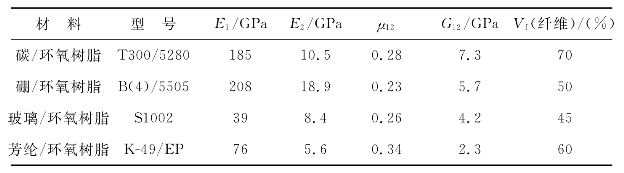
表10-2所示为几种单层复合材料的工程弹性常数的试验数据。

表10-2　几种单层复合材料的工程弹性常数

(www.xing528.com)

利用坐标变换，可以求得材料在任意方向上的应力应变关系。在对层合板进行应力应变分析时，需要用到这样的关系。图10-3（a）所示为材料主轴坐标系与整体参考坐标系之间的关系。θ表示从x轴转向1轴的角度，以逆时针为正。图10-3（b）所示为相应的应力分量。略去具体推导，可以得到

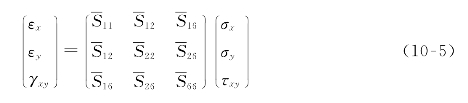
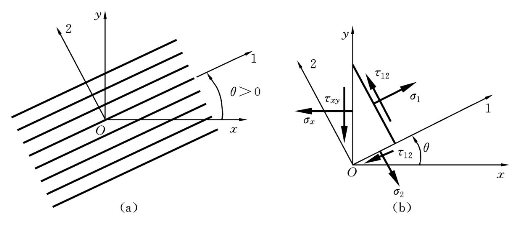
图10-3　两种坐标系之间的关系

式中：为变换柔度系数。

各变换柔度系数分量按以下公式求得：

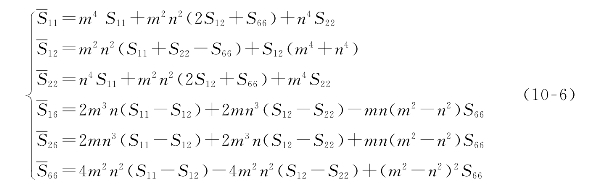
式中：m=cosθ，n=sinθ。

对式（10-5）求逆，得到

式中：为变换刚度系数。