加载频率对高温疲劳裂纹扩展的影响分析

高温疲劳的另一特征是裂纹扩展结果受加载频率的影响较大。室温下的裂纹扩展主要依赖于循环周次，而高温下的裂纹扩展与时间相关。在一定条件下，循环周次与时间这两方面因素均起作用。以下基于弹、黏塑性理论对裂纹尖端的应力应变进行数值分析，并利用黏塑性应变范围和J积分范围对不同加载频率下的试验结果进行分析，讨论用这两种参数表征裂纹扩展的有效性。

不同频率下的工业用钛材料疲劳裂纹扩展速度结果如图8-25所示。

图8-25　加载频率对裂纹扩展速度的影响

当加载频率较大时，裂纹扩展速度较小。对于裂纹扩展过程中加载频率发生变化，如由20 Hz变为2 Hz的情况，变化刚开始时，其裂纹扩展速度dl/dN较频率恒定（2 Hz）时的dl/dN还要大。反之，加载频率由2 Hz变为20 Hz，变化刚开始时的dl/dN较频率恒定（20 Hz）时的dl/dN还要小。随着加载的继续，dl/dN趋近于变化后的恒定频率下的dl/dN值。为计算黏塑性应变范围和J积分范围，首先应用弹黏塑性理论建立材料的本构关系。材料应变硬化效果用如下多层模型进行描述，如图8-26所示。将材料作为n个理想塑性杆的并联集合体来考虑，设杆i的体积占有率设为t i（t1+t 2+…+tn=1）。各杆的杆长和杨氏模量相同，作用于杆i的应力和弹性应变、塑性应变、初始屈服应力分别为Yn），当杆k发生屈服时，杆1到杆k-1均已屈服，它们承担的应力是各自的屈服应力与体积占有率的乘积Yjt j，而杆k+1到杆n尚处于弹性阶段，其应力为Yk乘以各自的体积率，因此全应力σ（k）可由下式求得：

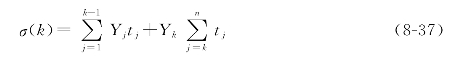
图8-26　弹塑性变形的多层模型示意图

将黏塑性材料的弹性应变记为εe，黏塑性应变记为εvp，全应变记为ε，全应力记为σ。一般应力状态下的应力应变关系用矢量形式表示为

(www.xing528.com)

采用Mises屈服条件时有

式中：F（σ，c）为屈服函数；为Mises等价应力；σ*为材料的屈服应力；c为反映加载路径的参数。

Perzyna给出的黏塑性应变速度为

图8-27　裂纹扩展速度与黏塑性应变幅值的关系

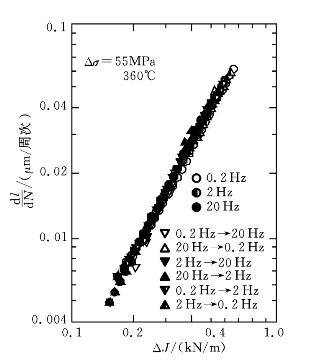
图8-28　裂纹扩展速度与J积分范围的关系