【摘要】:对于较长的裂纹,ΔKth为材料常数,记为ΔKth∞,则有在双对数坐标系中,门槛应力与裂纹长度关系曲线呈一斜向下的直线。尺寸小于a0的裂纹称为短裂纹。实际上,短裂纹的尺寸有一个范围,短裂纹的扩展特性不同于长裂纹,门槛应力既不等于光滑试样的疲劳极限,又不等于由式所确定的值。Tanaka等人[9]根据微观理论分析和试验,得到疲劳裂纹扩展的门槛应力以及门槛应力强度因子的表达式,以下是推导过程。
疲劳裂纹扩展的门槛应力记为Δσth,则门槛应力强度因子形式上写为
![]()
为简便起见,式(8-11)没有考虑形状修正因子。对于较长的裂纹,ΔKth为材料常数,记为ΔKth∞,则有

在双对数坐标系中,门槛应力与裂纹长度关系曲线呈一斜向下的直线。随着a的减小,门槛应力增大,当a小到某个值a0时,Δσth就与光滑试样的疲劳极限σ0相等,因此有

a0又称为过渡裂纹尺寸。
以软钢为例,ΔKth∞=6 MPa·m1/2,σ0=210 MPa,由此计算出a 0=0.26 mm,即对软钢而言,只有当裂纹尺寸大于a0时,线弹性断裂力学的概念才适用,裂纹扩展的门槛应力才可以利用式(8-12)来确定。尺寸小于a0的裂纹称为短裂纹。
式(8-13)所示的处理方法是一种近似的和简单的方法,该式称为Smith模型。实际上,短裂纹的尺寸有一个范围,短裂纹的扩展特性不同于长裂纹,门槛应力既不等于光滑试样的疲劳极限,又不等于由式(8-12)所确定的值。(https://www.xing528.com)
Tanaka等人[9]根据微观理论分析和试验,得到疲劳裂纹扩展的门槛应力以及门槛应力强度因子的表达式,以下是推导过程。
当裂纹扩展应力在门槛值附近时,认为裂纹尖端的滑移在晶界处受到阻碍,如图8-18所示。考虑滑移带与裂纹在同一平面上的情形(见图8-18(b)),当裂纹处于平衡状态时,有


图8-18 裂纹扩展门槛值模型

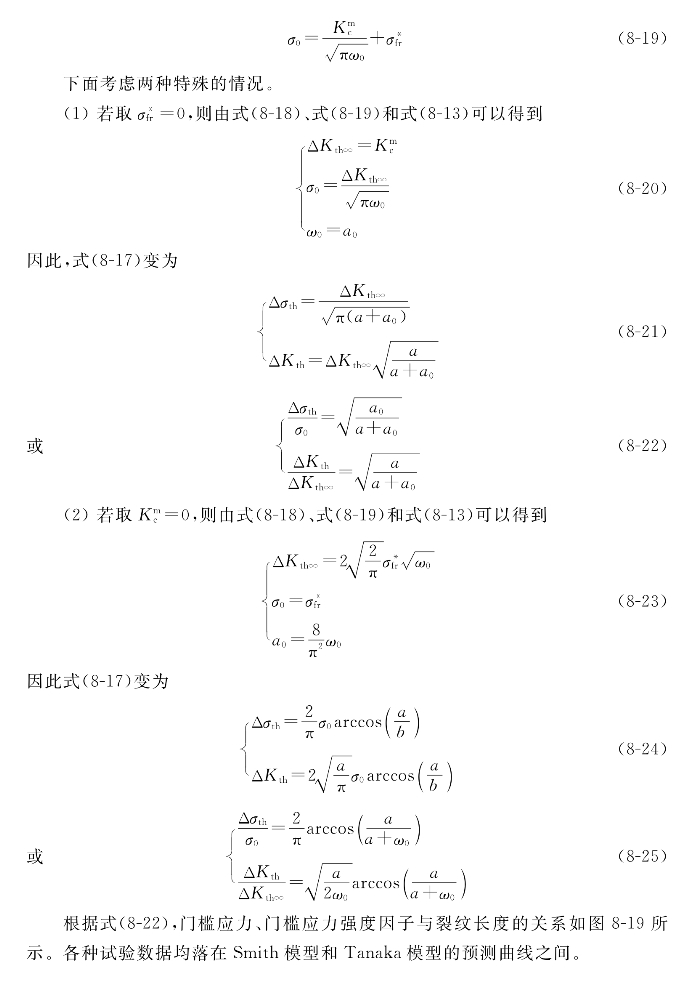

图8-19 无量纲化门槛应力、门槛应力强度因子与裂纹长度的关系
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




