应用断裂力学研究疲劳裂纹扩展

如前所述，疲劳裂纹的扩展是裂纹尖端发生循环塑性变形的结果。但这种塑性变形局限于裂纹尖端附近的区域，因此，若满足小范围屈服条件，可以应用断裂力学的概念和方法来对疲劳裂纹扩展进行分析。因为是循环加载，应力强度因子以其幅值ΔK来代表，裂纹扩展速度与ΔK之间存在以下关系：

式中：m=2～4；C为常数。式（8-3）称为Paris-Erdogan方程。

在双对数坐标系中，dl/dN与ΔK的关系曲线图分为三个区域（见图8-13）。在Ⅰ区，ΔK较小，dl/dN也较小，当ΔK小于临界值ΔKth时，dl/dN=0，ΔKth称为应力强度因子门槛值（threshold stress intensity factor）。ΔKth越大，表明材料阻止疲劳裂纹扩展的能力越强。门槛值和疲劳极限都是材料的疲劳抗力指标，前者可用于含裂纹构件的无限寿命设计，后者可用于光滑构件的无限寿命设计。Ⅱ区是疲劳裂纹亚稳态扩展区，其扩展规律由式（8-3）表示。Ⅲ区是高ΔK区，在这个区域dl/dN较大。当Kmax＞Kc，即ΔK＞（1-R）Kc时，材料将发生最终断裂，Kc为静态断裂韧度。为了求式（8-3）中的材料常数，通常按ΔK=常数来进行试验。这时，因为裂纹长度不断增大，需要在试验过程中逐步降低载荷，以满足ΔK=常数的要求。

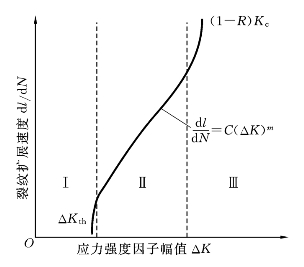
图8-13　dl/dN-ΔK关系曲线

为了考虑平均应力的影响，对式（8-3）进行修正，得到

受塑性变形影响，裂纹尖端周围存在残余应力，因此，裂纹在外应力不等于零时也可能发生闭合。裂纹扩展只有在裂纹张开时才发生，为考虑裂纹闭合的影响，用有效应力强度因子ΔKeff来替代ΔK，得到

(www.xing528.com)

图8-14所示为由式（8-5）绘制的dl/dN-ΔKeff关系曲线。

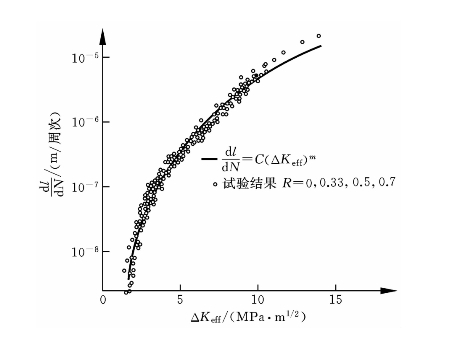
图8-14　dl/dN-ΔKeff关系曲线［7］

将代入式（8-3），假定m＞2，积分后求得裂纹扩展寿命Nf，即

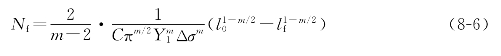
式中：l 0、l f分别为初始裂纹长度和临界裂纹长度。

考虑到，式（8-6）变为

在双对数坐标系中，Nf-ΔK0关系曲线为一直线，这也是一种S-N曲线。