如何确定材料的疲劳极限与S-N曲线？

在疲劳试验中，根据一个循环周期内应力的最大值与最小值（见图8-2），定义如下各参数。

应力幅值　

应力振幅　

平均应力　

应力比　

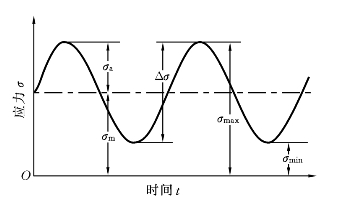
图8-2　循环应力

疲劳试验结果通常表示为循环应力振幅与对应的寿命（断裂时经历的循环周次）的关系，即S-N曲线（见图8-3）。如果断裂循环周次趋于无穷大，则对应的应力振幅称为疲劳极限（fatigue limit）。若应力振幅小于疲劳极限，材料就不会发生疲劳断裂。对于钢铁材料，S-N曲线由斜向下的曲线向水平线的转变通常在N=106～107时发生，习惯上将循环周次为107而不发生断裂的应力振幅上限定义为疲劳极限。对于非金属材料，S-N曲线没有水平段，这时，指定断裂循环周次为107或108，与其对应的应力振幅定义为疲劳强度（fatigue strength）。疲劳极限存在与否与材料有无屈服点密切相关，一般说来，有屈服点的材料存在疲劳极限，没有屈服点的材料在S-N曲线上没有水平段，即不存在疲劳极限。

图8-3　发生疲劳断裂和形成滑移带时的S-N曲线

（低碳钢，平面弯曲加载）

在发生疲劳断裂之前，材料表面已发生大量滑移，形成了滑移带（slip band）。对于光滑试样，正是滑移带中产生的裂纹，以及裂纹的长大与合并才导致了最终的疲劳断裂。在图8-3中，形成滑移带时的S-N曲线也一并示出了。疲劳断裂是疲劳损伤不断累积和加重的结果。

例8-1　A2026-T6铝合金的S-N曲线由以下经验公式描述：

在400 r/min的加载频率下，材料试验结果为：Δσ=310 MPa时，Nf=104；Δσ=230 MPa时，Nf=107。飞机机身构件中用到同一材料。若飞机每天飞行16小时，受疲劳载荷作用，Δσ=180 MPa，加载频率为400 r/min，试估算飞机寿命。

解　利用已有数据，确定经验公式中的常数a、c，进而估算飞机寿命：

(www.xing528.com)

一般以N 0=105为界来区分高周疲劳破坏与低周疲劳破坏。循环周次大于N0的疲劳破坏称为高周疲劳破坏，小于N0的疲劳破坏称为低周疲劳破坏。在高周疲劳中，应力振幅较小，几乎不产生塑性应变。高周疲劳破坏在宏观上表现为脆性断裂。对于低周疲劳，材料的疲劳破坏以及疲劳寿命取决于塑性应变的大小，此时应力与应变的关系如图8-4所示。

图8-4　低周疲劳下的应力应变滞回曲线

应变幅值分为弹性部分和塑性部分，即Δε=Δεe+Δεp，其中Δεp在低周疲劳中起主导作用，它与断裂循环周次N的关系可表示为

式中：k约为1/2。式（8-1）称为Manson-Coffin公式。将式（8-1）应用到静拉伸的极限情况（见图8-4中的曲线AB），则Δεp=εf，N=1/4，由此确定式（8-1）右端的常数为εf/2，因此，式（8-1）可写为

根据式（8-2），给定Δεp，可以估算相应的寿命N。

347不锈钢的低周疲劳Δεp-N关系曲线如图8-5所示。

图8-5　347不锈钢低周疲劳Δεp-N关系曲线［3］

例8-2　合金材料低周疲劳满足关系，若Δεp=5×10-3，求相应的寿命Nf。

解　　

对于低周疲劳，控制破坏的载荷参数不是应力幅值，而是应变幅值。在Manson-Coffin公式中载荷参数也是以应变幅值来表示的。在应力循环条件下，材料的静强度是决定疲劳寿命的主要因素，而在应变循环时，材料的韧度（εf）对疲劳寿命起决定性作用。

应力（stress）、应变（strain）及滑移（slip）这三个词的英文单词均以s开头，广义的S-N曲线包含了这三种情况。