蠕变裂纹扩展的研究进展

蠕变断裂一般是许多晶界微裂纹合并而导致的破坏现象。若是缺口试样，由于应力集中效应，缺口根部会产生一条主裂纹，在主裂纹的前方，晶界处形成的微裂纹与主裂纹发生汇聚而引起裂纹的扩展，最终导致蠕变断裂。蠕变裂纹扩展可用断裂力学的方法进行分析，即

图7-10所示为应用式（7-11）绘制的铜的蠕变裂纹扩展曲线。

图7-10　铜的蠕变裂纹扩展

蠕变会造成应力松弛，若不考虑裂纹尖端的应力集中效应，假定蠕变破坏由最小截面上的净应力σnet所控制，则σnet一定时，尺寸大小不相同但形状相似的两个试样将具有相同的裂纹扩展速度。图7-11所示为18-8不锈钢在环境温度为650℃、载荷一定的条件下的蠕变裂纹扩展试验结果，所采用的是相似的试样。图7-11（a）所示为利用应力强度因子K进行分析整理后得到的结果。对于每个试样，裂纹扩展速度大致落在一条直线上，但不同试样之间的差别很大。用σnet进行分析的结果如图7-11（b）所示，数据的分散度较图7-11（a）所示的结果大大减小。在相同σnet下，尺寸不同的试样，其最小和最大裂纹扩展速度仍有约10倍的差别。

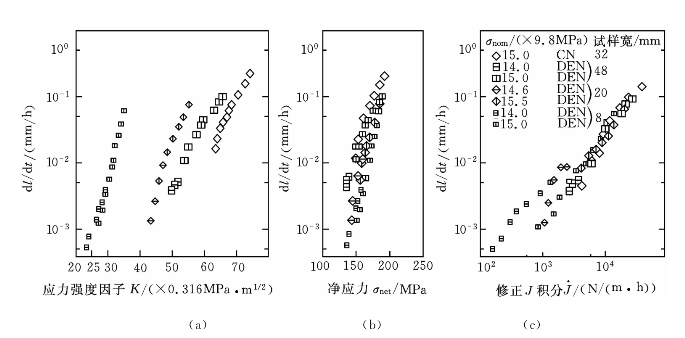
图7-11　18-8不锈钢的蠕变裂纹扩展试验结果

用修正J积分进行分析的结果如图7-11（c）所示，同一修正J积分、不同试验条件下裂纹扩展速度的差别远小于K基准或净应力基准下裂纹扩展速度的差别，因此，在蠕变条件下，修正J积分是较好的控制裂纹扩展的参数。修正J积分按下式定义：

或由变形功率定义为(www.xing528.com)

只要测得曲线，就可以进行相关计算。

在稳态蠕变阶段，假定单向应力状态下的应变速度和应力的关系为

则裂纹尖端的应力和应变速度分别为

式（7-14）中的n远大于1（在10左右），因此1/（1+n）≈0，n/（1+n）≈1，应力分布近似为均一分布，而应变速度与成正比，与距离成反比。由于蠕变会导致应力松弛，在裂纹尖端几乎没有应力集中，而存在应变集中。与大致成正比例关系。图7-11（c）中，数据落在斜率约等于1的斜线上，表明裂纹扩展速度与应变速度也成正比例关系。

图7-12所示为18-8不锈钢在环境温度为650℃时蠕变裂纹扩展的断面显微照片。在稳态扩展阶段，蠕变破坏表现为晶界破坏。

图7-12　18-8不锈钢蠕变裂纹扩展断口照片［7］