塑性变形机制与裂纹尖端塑性区尺寸

如图4-17所示，与裂纹尖端的变形相关的因素包括：原子、位错、亚晶界、亚晶粒、滑移带、晶粒、夹杂、孔洞和作为连续体的多晶体。为从宏观上分析裂纹尖端的塑性变形对应力强度因子的影响，假定裂纹尖端的材料为均匀各向同性的弹塑性体。

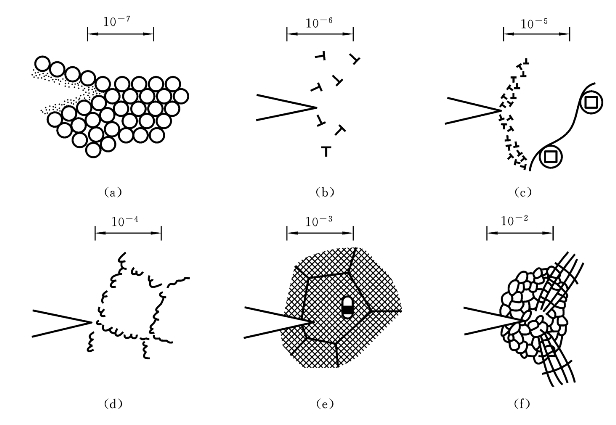
图4-17　裂纹尖端塑性变形的不同尺度影响因素（单位：cm）

（a）原子；（b）位错；（c）亚晶界；（d）亚晶粒、滑移带；（e）晶粒、夹杂、孔洞；（f）多晶体

当裂纹尖端处发生塑性变形时，裂纹自身的形状会发生变化（见图4-18）。考虑单晶体裂纹试样受到垂直载荷作用，裂纹尖端两个对称滑移系开动的情形。如在面心立方晶格金属中，裂纹面方位为（001），两个滑移面方位分别为、（111）；裂纹尖端的最大切应力方向大致与两个对称滑移系的滑移方向一致。在图4-18（a）中，设AB滑移系首先开动，由此产生新生表面AA＇和BB＇（见图4-18（b））。之后，在应力较大的A＇处，另一滑移系开动，产生新生表面A＇A″和C＇C″（见图4-18（c））。在两个滑移系交替作用下，裂纹尖端发生塑性钝化并开口。

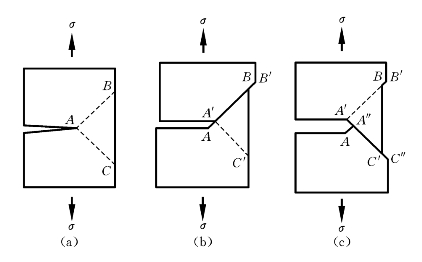
图4-18　裂纹尖端滑移面分离机制

以下计算裂纹尖端的塑性区大小。对于弹塑性材料，裂纹尖端会产生塑性变形，假定材料是理想弹塑性体，屈服应力为σys，则Ⅰ型裂纹尖端屈服区的尺寸（见图4-19）为

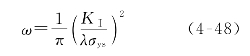
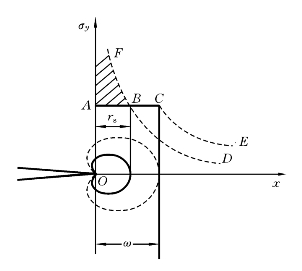
图4-19　应力松弛效应

式中：λ是塑性约束系数，为塑性区内最大应力与σys的比值。

式（4-48）推导如下。

对于平面问题，将式（4-16）代入主应力计算式，得到

采用如下的Mises屈服条件：

(www.xing528.com)

该结果正与式（4-48）一致。

如前所述，式（4-15）成立的条件是x≪a，因此，若ω＜x≪a成立，塑性区外侧的弹性应力场仍可用式（4-15）描述。ω≪a的条件表明，裂纹尖端的塑性区非常小，对塑性区外侧的弹性应力不产生影响。该条件称为小范围屈服条件，其具体表达式为

将具体数值代入rs和Keff的计算式，得

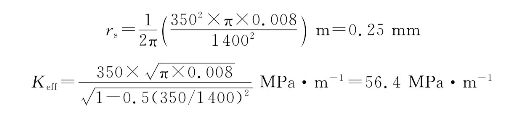
该结果与不做修正的K=55.5 MPa·m-1相比，仅高出2%。

对于本算例，ω=2rs=0.5 mm，a=8 mm，ω/a=0.063，满足小范围屈服条件，在计算应力强度因子时，可以不考虑塑性区修正的影响。

下面介绍求解裂纹尖端塑性区尺寸的Dugdale模型。

在平面应力条件下，设裂纹尖端塑性区呈带状（见图4-20）。裂纹原长2c，加上塑性区尺寸后变为2a。塑性区内的应力等于材料的屈服应力σys，在垂直的远场应力σ作用下，根据塑性区顶端无奇异性的条件（K=K＇（σ）+K″（-σys）=0），可以导出

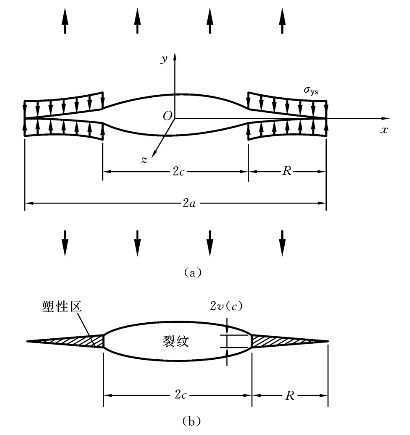
图4-20　Dugdale模型［4］

当σ≪σys时，通过级数展开并忽略高阶项，得到

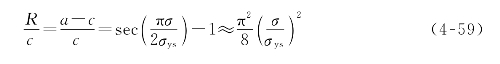
利用，式（4-59）可写为

对于平面应力问题，塑性约束系数λ=1。忽略系数的差别，该结果与由式（4-48）得到的结果一致。