应力强度因子与能量释放率的相关性

考虑平面应力Ⅰ型裂纹问题（见图4-11（a））。距离裂纹尖端x处的应力为

考虑裂纹扩展一小段长度Δa，在新的状态（见图4-11（b））下，点A处的开口位移为

因为Δa≪a，有K（a）≈K（a+Δa）。在图4-11（a）所示的状态下，点A位移v=0；而在图4-11（b）所示的状态下，点A处的应力σy=0。

从能量的角度考虑，裂纹扩展Δa所释放的能量，等于在如图4-11（c）所示的状态下裂纹表面力使裂纹重新闭合所做的功，即

图4-11　虚功原理和能量释放率

将应力和开口位移的表达式代入，经过演算求得

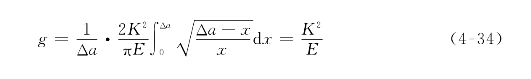
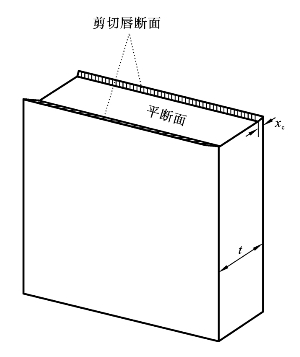
图4-12　平面应变下的平断面及表面的剪切唇断面

例4-2　说明如何利用试验方法，求紧凑型试样应力强度因子K=的修正系数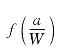。紧凑型裂纹试样如图4-13所示，图中。

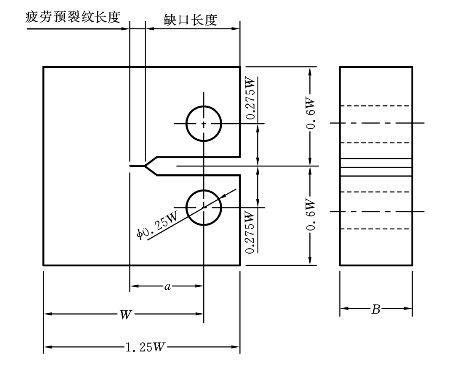
图4-13　紧凑型裂纹试样

解　利用第3章中式（3-5），即

(www.xing528.com)

例4-3　讨论相似试样的破坏应力的大小。

解　假定有两个试样，其材料相同，形状具有相似性，且有a 1/W1=a2/W2，2a1＞2a 2，如图4-14所示。由式（4-24），应力强度因子可以表示为

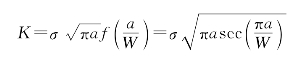
图4-14　有限板中心裂纹试样

由裂纹扩展条件K=Kc，可以得到裂纹体的破坏应力为

由此得到

即大试样的破坏应力较小。这个结果也称为尺寸效应。

例4-4　比较边裂纹试样与中心裂纹试样的破坏应力的大小。

解　半无限板中含长度为a的边裂纹，其应力强度因子为

无限大板含长度为a的中心裂纹，其应力强度因子为

两种试样的破坏应力之比为

表面裂纹的深长比小于0.5（a/c≤0.5）时，Φ的值较稳定，在1.18～1.28之间变化，这表明最大应力强度因子与表面长度没有太大关系，仅依赖于深度尺寸。