裂纹尖端应力场的分析和研究

式中：Z＇为Z的导函数。

在式（4-9）中，令y=0，有

考虑带裂纹的无限大板在远处受双向拉伸作用的情况，如图4-1所示。在裂纹面上，以下边界条件成立：

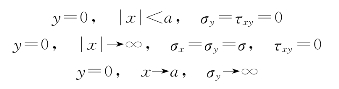
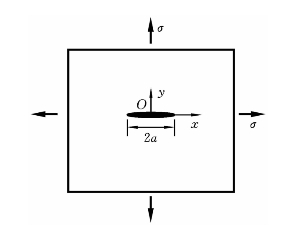
图4-1　裂纹体受双向拉伸作用

选取

则上述边界条件均成立，Z就是本问题的解。

对于带裂纹无限大板只在y方向受拉的问题，可以将其转换为在双向拉伸的基础上，叠加一无裂纹平板在远处受x方向压缩应力σ作用的问题来求解。由于裂纹尖端的应力奇异性对裂纹体的断裂行为起主导作用，而均匀压缩与应力奇异性没有关系，可以忽略，因此，通常将式（4-10）作为单向受拉裂纹体的解。

考虑图4-2（a）所示有长2a穿透裂纹的无限大板受拉伸应力σ作用的情况。以裂纹尖端作为原点，取坐标系O xy。利用式（4-10），并且将坐标原点移至裂纹尖端，则y=0时，应力分量σy沿x轴的分布为(www.xing528.com)

图4-2　无限大板穿透裂纹及裂纹尖端应力分布

式中：K为应力强度因子。K与加载应力σ及裂纹尺寸a有关，与局部坐标系的选取无关。对于有限宽平板，K写为式（4-2）所示的形式，即需要考虑形状修正因子。式（4-15）表明，裂纹尖端的应力场可以通过K唯一地确定。

式（4-15）还表明，当x=0时，不论K大小如何，都有σy=∞，而当x=x0时，该处的应力值由K唯一地确定，K较大，则σy较大，如图4-2（b）所示。此外，由式（4-14）知，即使两试样裂纹长度a不相等，通过调整外加应力σ的大小，使得两试样的K值相同，则裂纹尖端的应力分布就完全相同。

对于一般的三维问题，裂纹有三种基本的变形形式（见图4-3）：张开型（Ⅰ型）、剪切型（Ⅱ型）、面外剪切型（Ⅲ型）。与前述方法类似，可定义各基本变形下的应力强度因子，分别记为KⅠ、KⅡ、KⅢ。裂纹尖端一般处在三维应力状态，如图4-4所示。下面给出三种裂纹对应的应力的数学表达式。

对Ⅰ型裂纹，有

图4-3　三种裂纹变形形式

（a）Ⅰ型；（b）Ⅱ型；（c）Ⅲ型

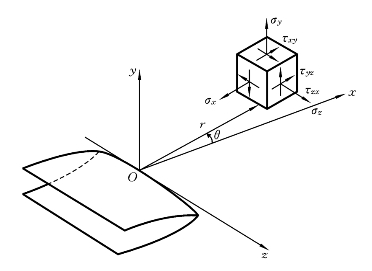
图4-4　三维裂纹尖端坐标及应力场