几种位错的应力场分析介绍，

1.刃型位错的应力场

除了位错芯（core）局部区域外，位错周围的应力应变场可用弹性力学的方法求解。芯部（半径为r0的区域）存在原子的不连续配置，而其他部分可作为连续的线弹性体来处理。晶体一般是各向异性的，为简便计，这里考虑各向同性的情况，而忽略各向异性的影响。这不仅对于直线状位错是较好的近似，对于曲线状位错，在小于曲率半径的近距离范围内，所得结果也有较好的近似性。图2-15所示为一刃型位错及所取的坐标系，假设该平面问题的Airy应力函数可以表示为变量分离的形式，即

图2-15　刃型位错坐标系

应力函数φ应满足如下极坐标系下的双调和方程（见附录A.10节中式（A-78）、式（A-79））：

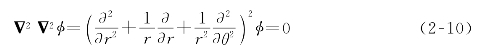
求解式（2-10），并利用平面应变条件和水平位移为b的条件，得到

由Airy应力函数φ（rθ）计算应力的公式为

由式（2-12）知，应力值与位置坐标r成反比。一般认为上述应力场的计算结果在环状区域（r0＜r≤r1）内是适用的。位错芯的半径r0估计为0.5～1 nm，环状区域的外径r1大约为10-5～10-4 cm。在r＞r1时，各应力分量可视为零。

2.螺型位错的应力场(www.xing528.com)

位错线沿z轴的螺型位错可通过下列操作形成：如图2-16所示，将弹性体沿O xz面剖开，剖面两侧沿z轴产生相对位移b后再胶合起来。由于螺型位错的变形是纯剪切变形，位移的x、y分量为零，即ux=u y=0，而uz≠0，所以以位移表示的平衡条件可简化为

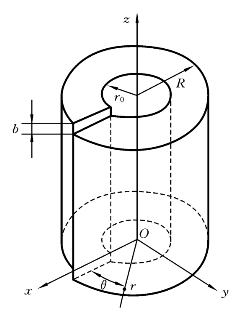
图2-16　螺型位错应力场计算模型

位移所要满足的螺型位错的边界条件为

该问题的解为

由此求得不等于零的应力分量为

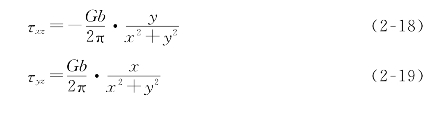
在圆柱坐标系中，有

可以看出，螺型位错没有正应力，且应力τrθ与θ无关。