如何优化非流水车间调度？

1）概述

非流水排序调度方法的基本原理与流水排序调度方法相同，亦是先通过作业排序得到调度表，然后按调度表控制生产过程运行，如果运行过程中出现异常情况，则需重新排序，再按新排出的调度表继续控制生产过程运行。因此，实现非流水排序调度的关键是求解非流水排序问题。

非流水排序问题可描述为：给定n个工件，每个工件以不同的顺序和时间通过m台机器进行加工。要求以某种性能指标最优为目标，求出这些工件在m台机床上的最优加工顺序。

非流水排序问题的求解比流水排序的难度大大增加，到目前为止还没有找到一种普遍适用的最优化求解方法。本节将介绍一种两作业m机非流水排序的图解方法，然后对非流水排序问题存在的困难进行讨论。

2）两作业m机非流水排序

（1）基本原理。两作业m台机器上的加工过程中，每一作业都需按照自己的工艺路线进行，每一工序使用m台机器中的某一台完成该工序的加工任务。如果没有出现两作业在同一时间段使用同一机器的情况，即没有资源竞争情况出现，两作业将沿各自的路线顺利进行，其作业进程的推进轨迹将是无停顿的直线轨迹。这种情况下，如果将两作业的推进轨迹合成起来即为两维空间中一条与水平线成45°夹角的直线轨迹，如图5-18所示，途中45°线后有一段水平直线是因为作业2结束后作业1仍继续合成轨迹。

在作业推进过程中，如果出现在同一时间段两作业需使用同一机器的情况，两作业之一必须让步，即让自己的推进过程停下来，让另一作业先使用该机器。于是停顿作业的推进轨迹上将出现停顿点，如图5-19中所示的J1轴上的圆点就是作业1的停顿点，其停顿时间为t1。这种情况下两作业推进轨迹的合成轨迹将出现折线。显然，含有折线的合成轨迹的总长度比不含折线的合成轨迹要长，这意味着作业推进的总时间将延长。

图5-18　无冲突时的作业轨迹

图5-19　有冲突时的作业轨迹

由此可知，为使完成两作业的总工期最短，应使合成轨迹的总长度最短。因此，为求出最优排序，应先找出所有可能的合成轨迹，然后计算每条轨迹的总长度，最后以总长度最短为目标选出最优合成轨迹。该轨迹对应的排序即为最优排序。

（2）求解步骤。根据上述原理，可将两作业m机非流水排序图解法的求解步骤归纳如下：

①画直角坐标系，其横轴表示J1加工工序和时间，纵轴表示J2加工工序和时间；

②将两作业需占用同一机器的时间用方框标出，表示不可行区；

③用水平线、垂直线和45°线3种线段表示两作业推进过程的合成轨迹。水平线表示J1加工、J2等待，垂直线表示J2加工、J1等待，45°线表示J1、J2同时加工。为使制造总工期最短，应使45°线段占的比例最大。找出所有可能的合成轨迹，图5-19中就存在两条合成轨迹，分别以实线和虚线表示；(www.xing528.com)

④以轨迹总长度最短为目标，通过直观对比和计算，从第3步确定的候选合成轨迹中找出最优合成轨迹；

⑤求解最优合成轨迹上的时间转折点，得到调度表。

（3）应用举例。

例已知2作业在6台机器上加工的工序、工时数据如表5-4所示，求使制造总工期最短的最优排序。

表5-4　加工工序、工时数据

解：图解排序过程如下：

首先按照上述求解步骤的第①②③步，找出有可能成为最优合成轨迹的候选轨迹。然后，以轨迹总长度最短为目标，通过直观对比和计算，从候选轨迹中找出最优合成轨迹，如图5-20所示。最后，求解最优轨迹上的时间转折点，结果如图5-21所示，据此市场调度表如表5-5和表5-6所示。

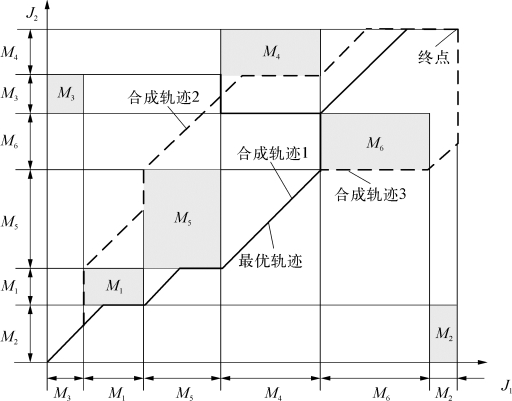
图5-20　图解排序与最优轨迹

图5-21　最优轨迹时间点分布

表5-5　时间表

表5-6　调度表