详细解释部分的术语和定义

1.轴、孔

如图1-1所示，上方的光滑圆柱形外、内尺寸要素是轴、孔，这很容易理解；而它们也包括非圆柱形的外、内尺寸要素（由两平行平面或切面形成的被包容面、包容面），这就较难理解了。

中间注尺寸的普通平键键宽的两平行平面，按照轴的定义为外尺寸要素；注尺寸键槽宽的两平行平面，按照孔的定义为内尺寸要素。图1-1下方注尺寸的矩形花键轴轴键宽的两平行平面，以及其大、小径相对应的断续圆柱形外表面，按照轴的定义均为外尺寸要素；注尺寸的矩形内花键键槽宽的两平行平面，以及其大、小径相对应的断续圆柱形内表面，按照孔的定义均为内尺寸要素。之所以把轴、孔的定义这样扩大，主要是为了便于对这种具有被包容面性质的单一尺寸采用轴的公差带，对这种具有包容面性质的单一尺寸采用孔的公差带。

2.偏差和尺寸公差

图1-1 轴与孔图解

a）轴 b）孔

由表1-1可知，偏差是以某一尺寸为被减数，其公称尺寸为减数，两者相减所得的代数差。按照代数学定义：a与b两个数无论是正还是负，a-b即称为a与b的代数差；而算术差为一个大数减去一个较小的数之差。上极限尺寸、下极限尺寸或实际尺寸都有可能比公称尺寸大，有可能比公称尺寸小，也可能与公称尺寸相等，所以此处用代数差是合适的。

尺寸公差是一个没有数学性质符号的绝对值，其图解如图1-2所示。无论公称尺寸为50mm的两个极限偏差均为正、均为负、一正一负、一正一零或一零一负，其尺寸公差均为0.02mm这样一段允许尺寸的变动量。按照代数学定义，不管数的符号为正还是为负，数的绝对值只讲其大小。据此，不应把尺寸公差作为正值，不能在尺寸公差数值之前冠以正号，若把尺寸公差称作“正公差”或“负公差”，那就更是错误的了。

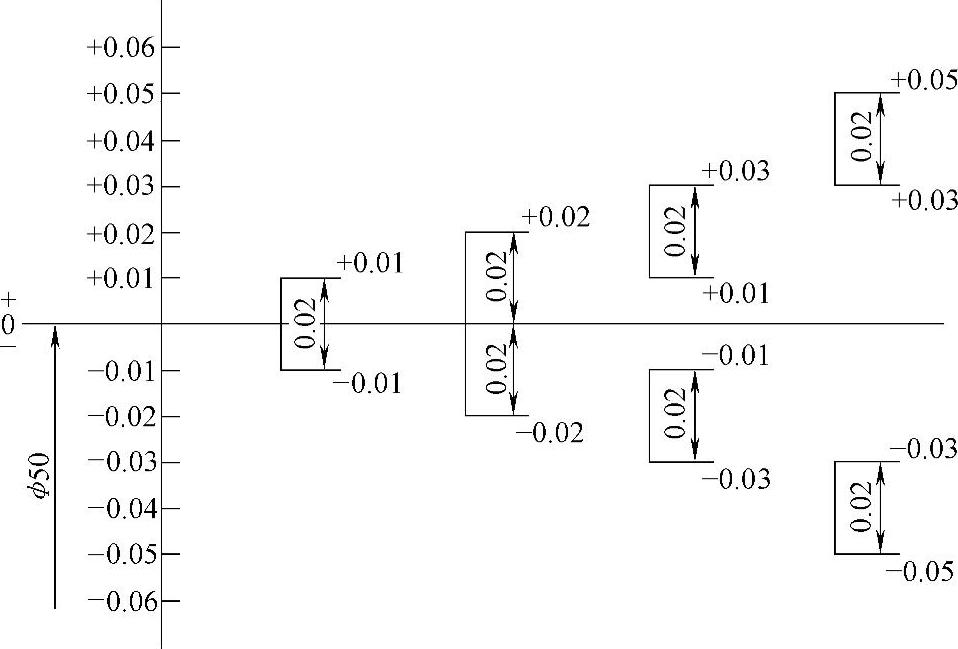
图1-2 尺寸公差图解

3.标准公差等级(www.xing528.com)

标准公差等级在极限与配合制中，应是对尺寸精确程度所做的一种排序，宜理解为标准公差分级；而“同一公差等级（如IT7）对所有公称尺寸的一组公差被认为具有同等精确程度”只是对其进一步说明。GB/T1800.1—2009只把上述“进一步说明”作为标准公差等级的定义，作者认为有所不足。

4.标准公差因子

标准公差因子是确定标准公差的基本单位，公称尺寸至500mm的标准公差因子计算式为：i=0.45׳D+0.001D；公称尺寸（大于）500～3150mm的标准公差因子计算式为：I=0.004D+2.1。由上述两个计算式可知，无论标准公差因子i或I，它们都是公称尺寸D（公称尺寸段的几何平均值）的函数；式中D以mm为单位代入，计算结果以μm表示（式中已经过单位换算）。各标准公差等级的公差数值（公称尺寸至500mm的IT01～IT4除外）均为该标准公差因子i或I的若干倍，且经过该标准中规定的修约规则而得。

5.间隙、过盈

由表1-1可知，无论间隙或过盈，孔的尺寸均作为被减数，相配合的轴的尺寸均作为减数，间隙是两者之差为正，过盈是两者之差为负。

在代数学中，一个数由其值与数学性质符号（正或负）所构成，如“+2”或“-2”这两个数，其大小均为2。在间隙或过盈计算中，如孔的尺寸减去相配合的轴的尺寸为“+0.02mm”，则表示此配合的间隙为0.02mm；如孔的尺寸减去相配合的轴的尺寸为“-0.02mm”，则表示配合的过盈为0.02mm；如某一配合孔与轴之差为“-0.035mm”，另一配合孔与轴之差为“-0.001mm”，前者表示过盈为0.035mm，后者表示过盈为0.001mm，自然前者过盈大，后者过盈小。

6.配合

GB/T 1800.1—2009对此术语基本采用原来标准GB/T 1800.1—1997的定义，该定义与ISO/286—1：1988国际标准相应术语的定义不同。由表1-1可知，它是指公称尺寸相同的，相互结合的孔和轴公差带之间的相对位置关系，如图1-3所示。它不是指单个孔与单个轴的结合关系，而是从区分配合类别的角度进行定义的。孔的公差带在轴的公差带之上的，为间隙配合（见图1-3a）；孔的公差带在轴的公差带之下的，为过盈配合（见图1-3b）；孔的公差带与轴的公差带相互交叠的，为过渡配合（见图1-3c）。单个孔与单个轴相互结合后只能具有间隙或者具有过盈，不可能过渡其间，如有间隙，则该结合可能属于间隙配合类，也可能属于过渡配合类；如有过盈，则该结合可能属于过盈配合类，也可能属于过渡配合类。

图1-3 配合类别

a）间隙配合 b）过盈配合 c）过渡配合