智力题具有趣味性、科学性和目的性,你可以根据自己的需要,选择一些相适应的内容来进行有方向性、目的性的练习,使自己在思维的各方面得到迅速提升。
其实做一些智力题,要重视分析这个问题的过程,以及主动地把生活现象也融入进去。练习得多了,思维自然就会开阔、灵活。
在解决问题时,我们要提醒自己不要受条条框框的限制,要养成独立思考的习惯,充分利用自己的知识、经验,同时借助外界的智慧来反复思考,直至问题得以解决。当你一旦打破条条框框的限制和思维定势,新奇的想法就会有了,问题也会迎刃而解。
如果遇事或解决问题,不考虑时间、地点、条件等具体情况的变化,而是一味根据习惯、常规、经验来想当然,那么很多问题就会难以解决。
例如要用6根火柴摆成4个三角形,你会怎么摆呢?思考时,如果有了足够的灵活性,能从平面转向立体进行考虑,就可以正确解决问题。
人们一般喜欢习惯性地接受现有观点和见解,而不大喜欢思考,一旦形成了思维定势,就会顺着定势的思维思考,不愿也不会换个角度和方向想问题,这样很难找到出路。
这里有一个问题,如图1-1所示,怎么样用4条直线且使线条不间断,将下面的等距点连接起来。按照习惯性的思维是不可能完成这个问题的,这就需要你开拓思路,从思维定势中走出来。

图1-1 4条直线把点连起来
大多数人的理解可能是这样的:所连的线仅在这九点所围成的空间之内。
在这里,我们要把线延伸出去,也如你的思维要打破条条框框的束缚一样,从那思维的框框里面走出来。
有了这个思维突破,再就是要选起点了。看图1-2,例如先连接3-5-7点,然后再连接8-9点,并延长线,再转向连接6-2点也延伸线,最后从1-4点返回到7点,难题就顺利解决了。
当然你也可以从其他点开始,一样可以到达成功的终点。
接下来想一想,有没有可能用更少的直线,把所有点都连起来呢?
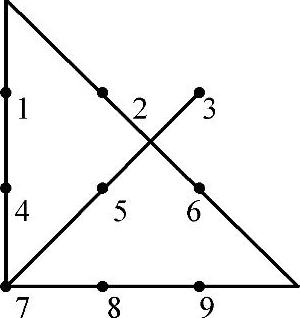
图1-2 一种连接方法
平时,对于我们的学习、生活和工作,一件事情只要去想,总是会有着很多好办法来完成的,这个过程会让你充满着思考的乐趣与小有成就的自豪感。当你把这件事做好之后,有没有仍然想过,是否还有更好的办法,或者是其他有创新性的办法呢?
如果我们找一支排笔,照着这九个点一刷,是不是一条直线挥洒而过就能把这九个点连起来呢?
人类的创新永无止境,唯有创新才能改变世界,创新改变内在的自我世界,继而改变外在的世界。
创新过程有时也会遇到这样的事:有的问题怎么思考也摆脱不了原有的框子。这时一种有效的办法是:把问题暂时搁置起来,让自己松弛下来,或转而思考其他问题,或与他人讨论交换意见,过些时间再来继续原来的难题,这样有助于摆脱习惯思维,有助于打破思维定势,使问题得到解决。
相信这个题目也是很多人在小时候就做过了的:
从1开始的整数,连续相加到100的总数是多少?
正确的思维是先头尾两两凑成同一数,然后算有多少对这样的数,再相乘就可以了,即101×50=5050。如果接下来要你计算从1到100内所有奇数之和,以及1到100内所有偶数之和呢?也许你会想,用同样的方法去做,不就能够很好地解决问题嘛。还是再多想一想吧,是否还另有出路。
一般来讲,以模仿思维为主的常规思维方法比较适合已知的世界,人们的思维活动通常是在模仿以前的成熟经验或他人的成功方法,这种复制成功的做法可以帮助人们节省思考摸索的时间和精力,少走弯路,从提高思维效率的角度来讲这是完全正确的。
是的,当我们发现了事物的规律,就可以充分而又灵活地利用了。用在与其相关、相似的事物上,有着意想不到的收获;而当你把这个规律、模式、方法跨行业运用时,或许会使问题奇迹般地迎刃而解。
但是,这种思维方式一旦进入未知的世界,由于人们没有可参照的模仿对象,它就不再适用,这时人们就需要启用一种新的思维方式来适应陌生的环境,这种思维方式就是创新思维。
麻雀虽小,五脏俱全,它的意思是别看麻雀虽然是小了点,但是其他相类似动物有的主要器官(如心、肝、脾、肺、肾)它都有。

那么引申一点,朋友你又想到了什么呢?为什么很多东西人们要事先做模型?遇到困难、麻烦的问题,我们可以把它简化、模型化,只要前后两者的共同结构和特点保持了就行,然后我们解决这个简化的问题,解决这个问题的方法就可以找到了,就能够用这个方法和规律轻松解决原来的难题。当然,这个后面的过程也许还会遇到和做模型时不一样的问题,或者说那个方法并不能解决原来那个难题的所有问题,我们要区别对待和解决。
最典型的例子是在医学界,研究一种病的机理、研发一种抗病药物,或者要试验某些药的特性,会先选择一些动物作为模型来实验,选择最多的是小白鼠。借助于动物试验的间接研究,以便更准确地观察动物的试验结果,并与人类疾病进行比较研究,有助于更方便、更有效地认识人类疾病的发生、发展规律,研究防治措施。在它们身上试验的结果,可以作为一个参考,甚至是一个同样也适合人类的结果。
现实中很多问题的研究和解决,大多都会选择先做模型。
所以,朋友,这就是模型带来的巨大魅力,往后你也可以大胆地来试一试。例如,一些不好理解的知识,可以借助做实验来理解。
当事物发展到一定时候,你依然可以沿用以前的经验来办事,但是,倘若你能转个弯,就会发现有更好的解决办法,这时你会有种豁然开朗的感觉。有如一盏灯火,照亮在黑夜道路中前行已久的你。这是一种多么美妙的感觉呀,愿这种感觉能时常来到你的心间。
让我们再回到刚才分析的那个问题:1到100连续整数相加,有了规律可循,1到100内奇数相加就容易了。那么1到100内偶数相加呢?能不能用连续整数相加的结果直接减去奇数相加的数呢?
呵呵,原来这么简单啊,朋友,你想到了吗?
事物的解决之道,最简单的办法往往是最好的办法。
最简单的办法往往也是最有效率、综合成本最小的。
现代人崇尚简约,能让生活更美好的一些小创意物品,总是让人无比喜爱。让我们的思维创意延伸到尽可能多的领域中吧。
朋友,给自己来个难一点又能确实开拓思维的大餐吧。
这里有12个玻璃球,特征相同,但有一个重量异常,与正常重30克的球相差5克。现在请你用一台没有砝码的天平称三次,把重量异常的那个球找出来!
由于不知道这个异常球重量是比正常球重还是轻,所以当天平两边放入数量相等的球时,要么一边重一边轻,要么两边一样重,即天平是否平衡会反映出来。
根据这个提示,在看下面详细分析之前,还是让我们自己先动动脑吧。如果能,倒是可以拿实际有重量差异的东西作演示,这样更直观,哪怕是写上标号的纸片也是行的。
有人这样称:把球分成A、B两组,A组8个球,B组4个球,把A组球平分在天平两个托盘中,如图1-3所示。这时会有两种情况:天平平衡和不平衡。

图1-3 将A组球平分放置于两边
若天平平衡说明接下来要称B组球,将B组球再平分在天平两托盘中,这时总有一边会重量轻一边重量重,这样行不行呢?(https://www.xing528.com)
显然不行,由于没有告诉我们重量异常的球,是重于标准球还是轻于标准球,没有一个标准、没有一个参照物,怎么比呢?
想一想前面称的一次不是天平平衡吗?这说明那8个球是一样重,可以作标准球。朋友,经过这样的提示你想到了下一步该怎么做了吗?
可以从那8个球中取两个放在天平一边,B组中任意取两个放在天平另一边,这时也有两种情况出现,平衡或不平衡。到这里就请朋友你自己分析吧,相信你一定能通过自己的分析,找出那个重量异常的球,甚至可能知道是比标准球重或者轻。在这一步里,尝试一下在左边放三个标准球,右边放B组中任意三个球,是否也能判断哪个球异常呢?
回到第一次测量,如果天平不平衡,说明重量异常球就在这8个球里,这可能就有些难了。朋友,还是请先自己动动脑想一想,动手试一试吧,不用急于看后面的分析哦。
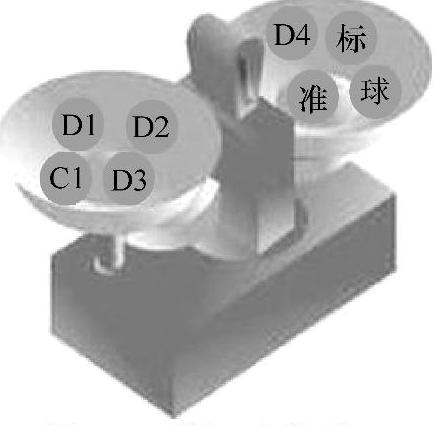
图1-4 第二次称重
现在假设天平是右边重于左边。我们把左边托盘里的四个球命为C组,右边为D组,编号为C1、C2、C3、C4与D1、D2、D3、D4。接下来得想一想每边放几个球,且怎么放了。
在将这两组球作标示后,接下来这样操作比较合适一些:如图1-4所示,将天平左边C组球中的C2、C3、C4取出,取右边盘中的D1、D2、D3放入左边托盘,右盘剩下D4,再取3个标准球放入右盘,作第二次测量。
回过头来分析第一次称的结果,左边轻,右边重,说明要么是左边的某一球轻于标准球,或右边某一球重于标准球。
进行第二次称重先假设天平平衡,因为D组球全部放于托盘中,说明D组球全部是标准球,同时说明是C组球有一个球轻于标准球,且异常球在C2、C3、C4中。朋友,这里想明白了吗?这时把这三个球中的任意两个球分放在两个托盘中,若再次平衡说明未测的C4为轻球,若不平衡,则轻的一边为轻球。
若第二次称重是左边比右边重,因为第一次测量时是左边轻或右边重,原右边D组球已全部在托盘中参与测量,说明异常球在D1、D2、D3中,且比标准球重,接下来的分析相信你一定可以出色完成。若第二次测量是右边重,说明D4就是异常球,重于标准球。
如果在第二次是这样放:把C1、C2、C3这三个球放在左边,再加入一个标准球。右边放入C4、D1与另外两个标准球。试着再分析一下,结果会是怎么样呢?还有,再深入分析一下,这样称法与上面的第二次称法各有什么特点,又有什么共同的特点呢?
路,总是很多条,有如象棋的棋局,一颗棋子有着多样走法,而每样走法又会使后面的布局、运筹各不相同。对于这些用来锻炼的题,或者是现在和以后遇到的实际难题,我们勤于思考下,也一样是多多益善呀。
这个思维题很有代表性,能全面地训练你的思维。虽然是难了些,但没关系哦,只要你融入了,就会慢慢地发现你的思维越来越灵活,能创造性地解决问题了。

思域无限,探索无止
在现实生活中,我们也要善于利用已知世界的东西,想办法解决面临的问题,借助外界的力量,来充实自己的能力。
有时,看似复杂的问题,换个角度,是能够用最简单、最质朴的方法来解决的。
现在有一个这样的物体,要你测量它的体积:它是由圆柱体、锥体、正方体、三角体等组成组合体。按照传统方法,人们会用公式来分别计算,然后再把分别算出的体积结果相加,便是那个组合体的体积了。朋友,你会怎么做呢?
如果把它放入装有水的量杯,问题是不是变得非常简单了?而此时你一定会有一种拨开云雾见天日的爽朗感觉,也犹如黑暗中突现一盏灯火照亮前程。朋友,当你有这种感觉,恭喜你进入了那种状态和境界。继续努力吧,后面的路将更精彩,更富有挑战性。

图1-5 切法示意图
分金条的故事
这是一个我们可以常在书上见到的问题,就是雇主有一根金条,要用来给帮他做事的工人付一星期七天的工资,每天都要付一次,现在你只能切两次,要怎么样做才能只切两次,又能每天付工资呢?我们通常的做法是,如图1-5所示,在七分之一处切一下,在七分之三处切一下,第一天付一块,第二天把有两份的付给他,昨天的那一块找回来。就这样如此类推,换三次后便完满地解决了问题。
我们看一看,初想一下似乎这个发工资的事情不可能完成,但这里用到了置换,拿两份换他的一份,这是解决问题的关键所在。
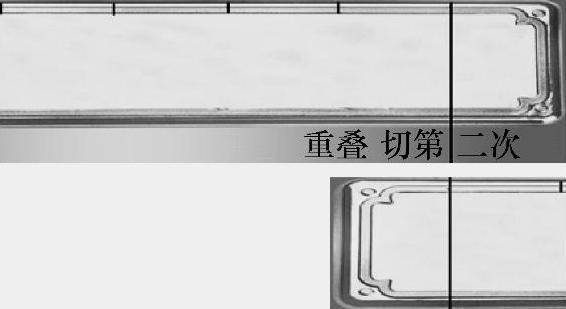
图1-6 稍作改变更具创意的切法
再想一想,还有没有其他的办法哟?我们这样试一下,第一次切七分之二处,第二次如图1-6所示,把两份的和五份的一边平齐叠放切一下,两份的又平分了,五份的也再一次切成一份跟四份,这样,我们就只要置换一次了。是不是这个办法比上面的更好呢?又好在哪里呢?
还是再想一想,我们的生活中,也一定会有诸如此类、同样也有曾令自己心动不已、为此找到更好办法的事例吧。让我们合上书,静下心来,把这个分金条故事的启发与我们现实生活联系起来,试着往更多的方面、更深处想一想。对,就这。样
现代社会中,我们会讲究高效率,在学习、生产、工作、生活中,很多东西都在不断地探索改进,能减少环节、能化繁为简,就是整合了资源,创造了效益,也就最大限度地利用了资源。电子技术的学习与实践,也一样地要时常探索新的理解方式、新的操作方法,不断提升自身素质和能力。
这世界上没有最好的,只有更好的。
话是这样说,但对于我们初学者来说,首先要做的,还是要脚踏实地地学,脚踏实地地做,而不是省事和“投机取巧”。只有基础打好了,相关的知识系统做扎实了,才更有可能去探索新的、更好的
曹冲称象的故事
古代曹冲称象的故事很多人都知晓,当时吴国的孙权送给魏国的曹操一只大象,长久居住中原的曹操从来没有看过这种庞然大物,好奇地想知道这个大怪物到底有多重?
于是,他对着臣子们说:“谁有办法把这只大象称一称?”
在场的人七嘴八舌地讨论着:有人回家搬出特制的秤,但大象实在太大了,一站上去,就把秤踩扁了;那时可没有那么大的秤,有人建议做一个大秤,有人说分成很多小块后再称。曹操喜欢大象的可爱模样,不希望为了称重而失去它。

小小曹冲在称象呢
正在大人们一筹莫展要放弃的时候,曹操7岁的儿子曹冲说:可以拉一只船过来,把大象牵上船,待船稳定后再在船身平水的两边位置各画一条线。然后牵下大象,再往船上装石头,直至船边画线平水的位置,把石头的重量一称,这就是大象的重量了。看似不可能的事情,就这样让他解决了。
这透露出一种智慧,是巧妙的转换思维运用。在一般人眼里,秤是用来直接称重的,而曹冲突破常理,来了一个重量转换,成功地解决一大难题。
我们在平时,也需要独立自主地选择学习内容,自主学习,需要更多接触外界的知识和信息,触类旁通,来培养自己的创造能力。
接下来,特意为你准备了下面几个题目,送给求知心切,已跃跃欲试的你:
(1)两个空心球大小及重量相同,但材料不同,分别是金球和铝球,这两个球用相同的绒布分别紧包着。在不破坏绒布的条件下用简易方法分辨出哪个是金的,哪个是铝的。
(2)假设在这本书上平均每翻一页上打个点要一秒,问这本书你可以用多少时间在每页上打完点?如果再快些,你有把握把时间缩短到大约多少来完成呢?有挑战性哦。
(3)有八个装着高品质手机印制电路板(PCB)的箱子,本来每块PCB的重量是相等的,但是有一箱因生产制作时出了差错,使这箱的每一块PCB厚度变薄了,该箱每块PCB会比正常的板要轻6g,因品质要求严格,必需找出,现在最少要称多少次才能找出这箱有问题的PCB。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




