拓展题解析：汉明码的编码与纠错

1.某编码的全部许用码字集合是C={000，010，101，111}，该码是线性码吗？是循环码吗？为什么？

解：（1）是线性码，满足封闭性，且监督码元（只有一位）a₀与信息组a₂a₁间的关系为a₀=a₂。

（2）不是循环码，因为码字010循环移位后不是其中的一个码字。

2.若一个行列监督码码元错误情况如图9-15所示，试问译码器能否检测出此错误？能否纠正？

解：（1）对于图9-15a所示的接收码字，译码器无法检测出其中的错误。因为在行列奇偶监督码中，只有当每行或每列中有奇数个错误时，才能检测出来，而图9-15a所示的行和列恰好都有偶数个错误，所以检测不出来。

（2）对图9-15b所示的接收码字，译码器不仅能检测出错误，而且还能纠正这些错误。因为每行和每列中的错误都只有一个，故通过行和列就能确定错误的位置。

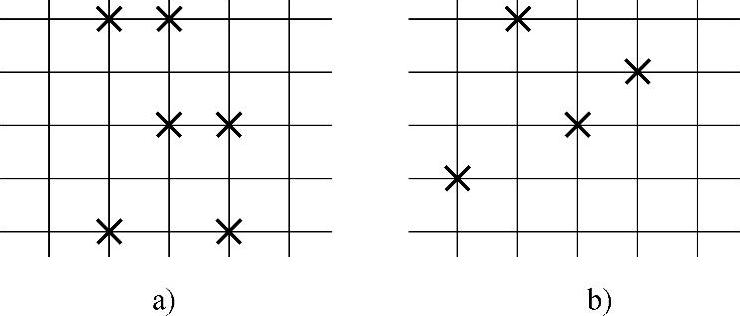
图9-15 行列监督码码元错误图样

3.将（7，4）汉明码的编码结果按行写入一个10行7列的存储阵列，每行一个码字，一共是10个码字。再按列读出后通过信道传输。若传输这10个码字时，信道中发生了连续15个错误，请问接收端解调并译码后，能译对几个码字？

解：能译对5个码字。15个连续错码通过交织分散到10个码字中，其中5个码字中各有两个错码，另5个码字中各有一个错码。因为（7，4）汉明码只能纠正每个码字中的一个错误，故可译对5个码字。

4.已知x⁷+1=（x+1）（x³+x+1）（x³+x²+1），试问共有多少种码字长度为7的循环码？并列出它们的生成多项式。

解：循环码完全由生成多项式决定，一个生成多项式产生一种循环码，故有多少种生成多项式就有多少种循环码。

码字长度为7的循环码的生成多项式g（x）应满足：g（x）是x⁷+1的因子，g（x）的常数项为1，g（x）是r=n-k次多项式。

显然，x⁷+1含有1次、3次、4次、6次因子，且其常数项均为1，因此可构成的循环码有：

（7，6）码：g（x）=（x+1）

（7，4）码：g（x）=（x³+x+1）或g（x）=（x³+x²+1）

（7，3）码：g（x）=（x+1）（x³+x+1）=x⁴+x³+x²+1

或g（x）=（x+1）（x³+x²+1）=x⁴+x²+x+1

（7，1）码：g（x）=（x³+x+1）（x³+x²+1）=x⁶+x⁵+x⁴+x³+x²+x+1

5.（1）已知长度为7的循环码的生成多项式为g（x）=x⁴+x²+x+1，若m（x）=x²，求其系统码字。

（2）码长为1023的汉明码的编码效率为多少？其最小码距为多少？纠检错能力如何？

（3）码字长度为8的偶校验码共有多少个码字？试写出其监督方程。

解：（1）由题意可知，n=7，r=4（生成多项式最高次），则k=3。

利用生成多项式直接产生系统码字多项式，再将多项式写成码字。

码字多项式为

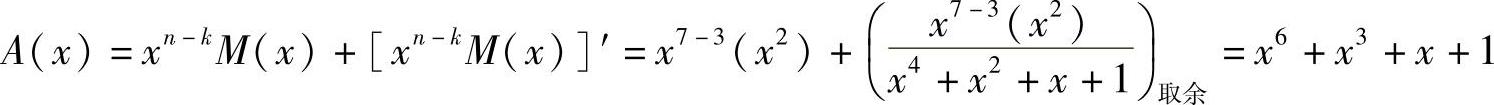
此码字多项式所对应的7位系统码字为1001011。

（2）由题意可知，n=1023，代入汉明码关系式n=2^r-1，得r=10，故编码效率为

无论码字长度为多少，汉明码的最小码距均为d₀=3。因此，若用于纠错，只能纠正码字中一个错误；若用于检错，最多能发现码字中的两个错误。

（3）由题意可知，n=8，对于偶监督码，不管码字长度为多少，码字中都只有1位监督码元，可见，信息位数为k=n-1=8-1=7，故码字总数为2^k=2⁷=128个。

设长度8的偶监督码字为a₇a₆a₅a₄a₃a₂a₁a₀，由于偶监督码字中“1”的个数为偶数，因此可得监督方程为

a₇⊕a₆⊕a₅⊕a₄⊕a₃⊕a₂⊕a₁⊕a₀=0

或 a₀=a₇⊕a₆⊕a₅⊕a₄⊕a₃⊕a₂⊕a₁

注：在编码一章中，常用“+”代替“⊕”。

6.（1）某线性分组码的码长为15，如欲纠正所有单比特错和双比特错，请问非零的伴随式（校正子）至少应该有多少个？

（2）假设信道是随机差错的二元信道，其误比特率为10^-3，请问发送0000000时，收到的7个比特不是全零的概率为多少？

解：（1）为能正确译码，不同的错误图样需对应不同的伴随式。分组码的码长为15时，码字中仅发生一比特错误的图样有C¹₁₅=15个；码字中仅发生两比特错误的图样有C²₁₇=105。故为能纠正发生在码字中的单比特和双比特错误，非零伴随式至少应有15+105=120个。

（2）当误比特率为P_e时，每个比特发生错误的概率为P_e，正确传输的概率为1-P_e。故发送7个“0”，而全部正确接收的概率为（1-P_e）7=（1-10^-3）7≈1-7×10^-3。因此，收到7个比特不是全零的概率为1-（1-P_e）7≈1-（1-7×10^-3）=7×10^-3。

7.某线性分组码的全部码字如下：

（1）求最小汉明距离。

（2）求编码效率。

（3）写出该码系统码形式的生成矩阵。

解：（1）线性分组码的最小码距等于非全零码的最小码重，故该线性分组码的最小码距为d₀=4。

（2）全部码字为8个，因此k=3。又知码长n=7，所以编码效率为η=k/n=3/7。

（3）当信息为100时，系统码码字的最高3位应为100，与上述所给码字对比可知，只有码字1001011符合条件。类似地，当信息为010和001时的系统码码字应分别为0101110和0010111。又根据编码方法A=MG可知，这三个码字即为系统码生成矩阵G的三行，由此可得系统码形式的生成矩阵（典型生成矩阵）为

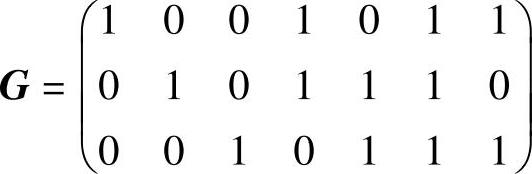
8.已知某（7，4）码的生成矩阵为

（1）将矩阵G转化为系统生成矩阵（典型生成矩阵）。

（2）写出该码中前两个比特为00的所有码字。

（3）写出该码的校验矩阵H。

（4）求接收码字B=[1101011]的伴随式。

解：（1）（7，4）系统码生成矩阵的形式应为

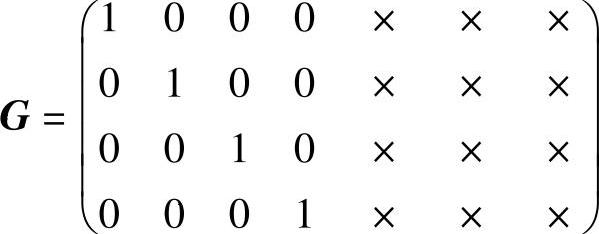其中“×”为“1”或“0”

对照系统码生成矩阵，对给定生成矩阵的行做线性变换即可得出系统码生成矩阵。

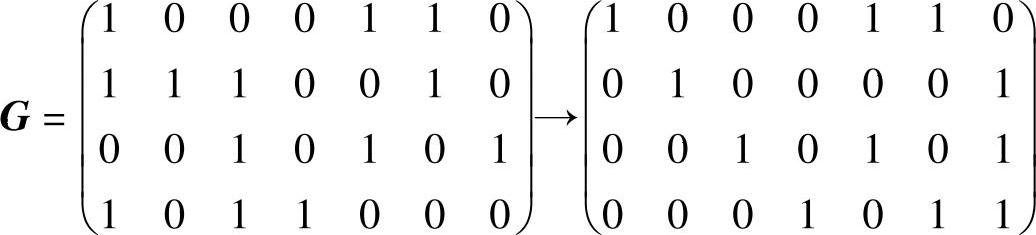
注：第一、三行加到第二行，第一、三行加到第四行。

（2）对系统码而言，码字的前两个比特为00即意味着信息的前两个比特为00。满足条件的信息码组有0000、0001、0010、0011，则由A=MG得

因此，该码中前两个比特为00的所有码字为0000000、0001011、0010101、0011110。

（3）由系统码生成矩阵

得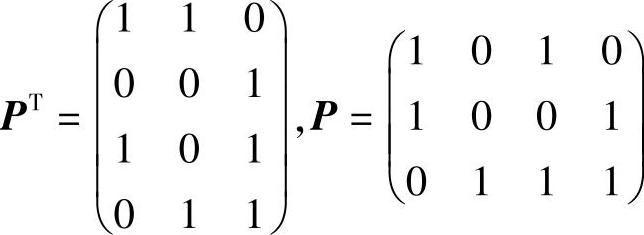

则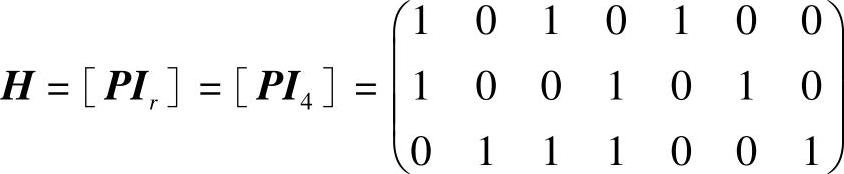

（4）由S=BH^T得(www.xing528.com)

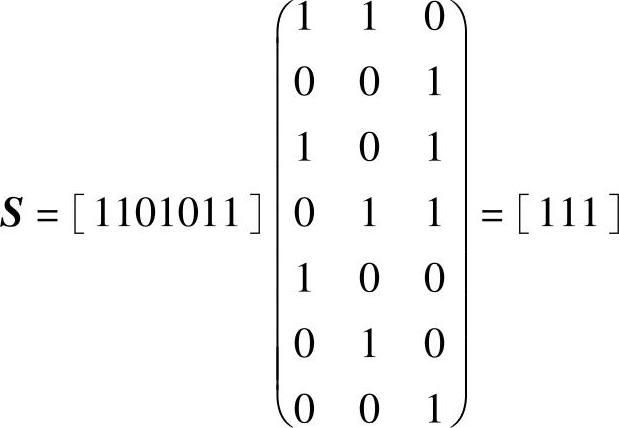
9.已知（7，4）系统循环码，其生成多项式为g（x）=x³+x+1。

（1）求信息0111的编码结果。

（2）若译码器输入是0101001，求码多项式模g（x）所得的伴随式，并给出译码结果。

（3）写出该码的系统码形式的生成矩阵及相应的监督矩阵。

解：（1）系统循环码的监督多项式为

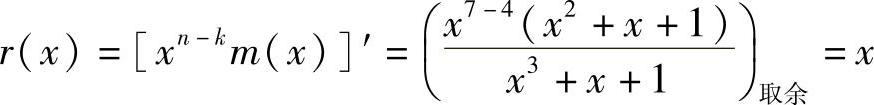
其中m（x）=x²+x，n=7，k=4。

因此，码字多项式为

A（x）=x^n-km（x）+r（x）=x³（x²+x+1）+x=x⁵+x⁴+x³+x

所以信息0111对应的7位码字为0111010。

（2）接收码字多项式为B（x）=x⁵+x³+1，其伴随多项式为

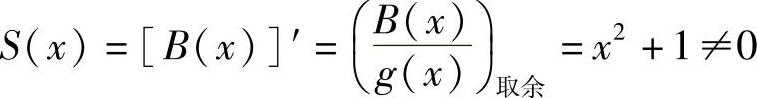
显然，接收码字中有错误。由S（x）=[e（x）]′可求得，当e（x）=x⁶（最高位有错）时，对应伴随式为S（x）=x²+1。可见，接收码字的最高位有错，因此，译码后的码字为1101001。

（3）由生成多项式构建的生成矩阵为

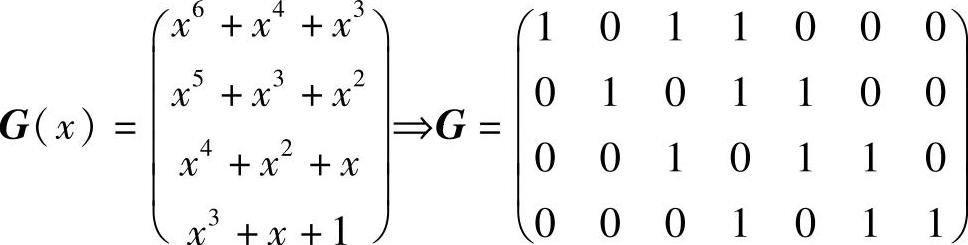
将第三行、第四行加到第一行，再将第四行加到第二行，得典型生成矩阵为

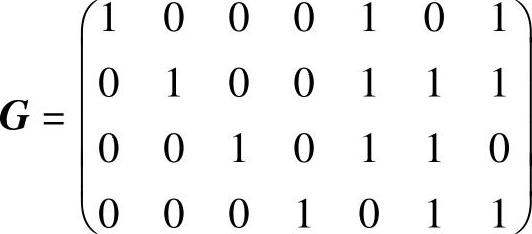
由此得到典型监督矩阵为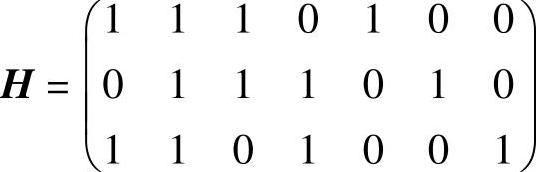

10.已知（7，4）循环码的全部码字为

请写出该循环码的生成多项式g（x）以及对应系统码的生成矩阵G。

解：生成多项式是次数最低的码字多项式（全零码字除外）。因此码字0001011对应的多项式就是生成多项式，即g（x）=x³+x+1。

由生成多项式构造生成矩阵，再将其各行写成码字形式，即

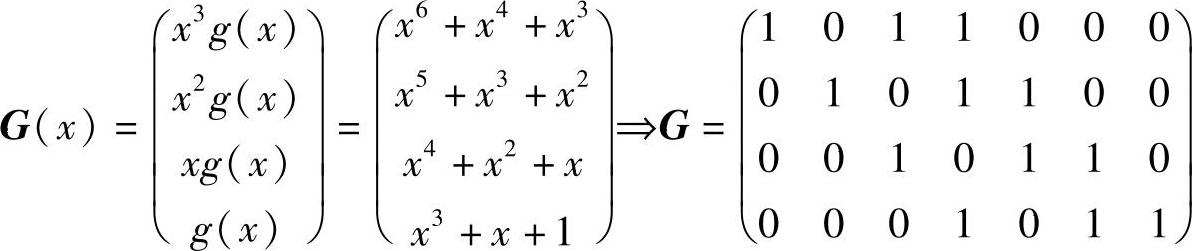
将第三行、第四行加到第一行，再将第四行加到第二行，得到典型矩阵为

11.已知（7，4）循环码生成多项式g（x）=x³+x+1。

（1）求其生成矩阵及监督矩阵。

（2）写出该循环码的全部码字。

（3）求该码的最小码距及纠检错能力。

解：（1）由生成多项式构建生成矩阵

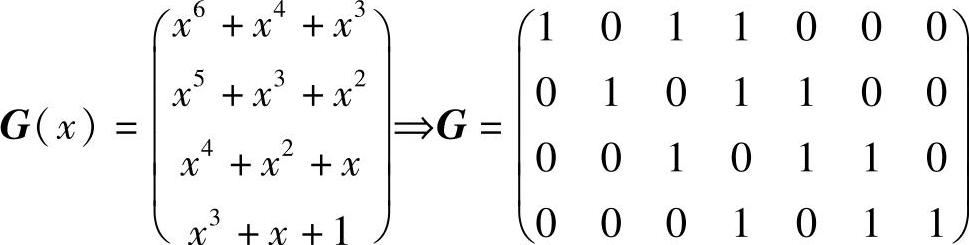
将第三行、第四行加到第一行，再将第四行加到第二行，得典型生成矩阵为

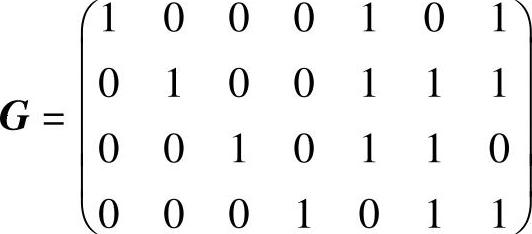
由此得到典型监督矩阵为

（2）将4位信息的不同组合M=[0000]～[1111]共16种分别代入A=M·G，得到16种码字为

（3）最小码距d₀等于非全零码字的最小码重，由上述码字可得d₀=3。故用于检错，最多能检测两位错误；用于纠错，最多能纠正一位错误。

12.已知某（n，3）循环码的生成矩阵。

（1）确定n的值，并求编码效率η。

（2）确定该码的生成多项式g（x）。

（3）求输入信息为011时相应的系统循环码码字。

解：（1）生成矩阵的列数等于码字长度n，故n=7。编码效率η=k/n=3/7。

（2）循环码有如下性质：①生成矩阵中的每一行都是一个码字。②循环码的任一码字循环移位后仍然是一个码字。③生成多项式是次数为r=n-k=7-3=4的码字多项式。根据这些性质，生成矩阵第一行对应的码字循环左移两位后得到码字0010111，此码字多项式即为生成多项式，即g（x）=x⁴+x²+x+1。

（3）当信息为011时，系统循环码的码字多项式为

A（x）=m（x）x^n-k+[m（x）x^n-k]′=m（x）x⁴+[m（x）x⁴]′

式中，m（x）=x+1；[m（x）x⁴]′=x³+1。因此有

A（x）=x⁵+x⁴+x³+1⇒A=0111001

13.如图9-16所示，输入是独立等概取值0、1的二进制码元序列，信息速率为2Mbit/s，首先进行卷积码编码，再经单/双极性变换器，最后进行16QAM调制。

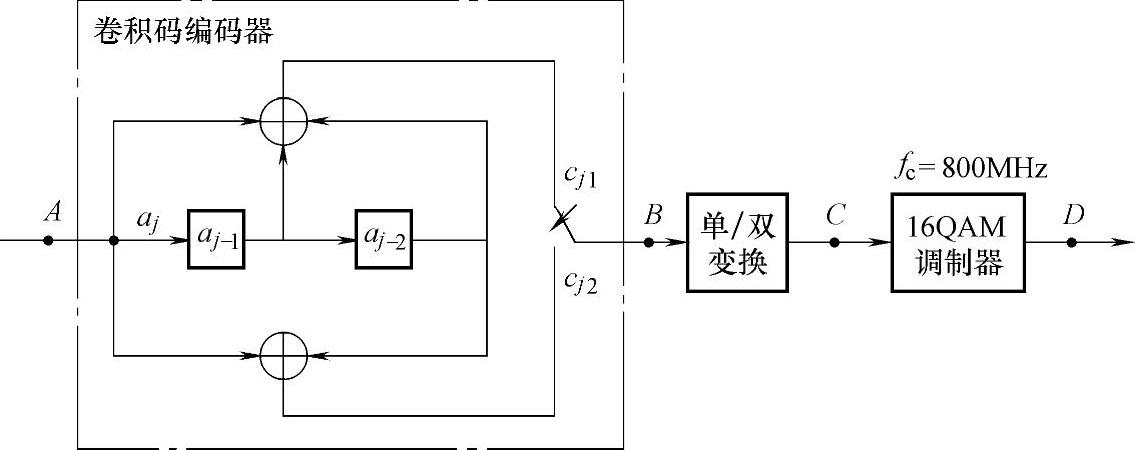
图 9-16

（1）写出卷积码的监督关系。

（2）求输入信息为1100101…时对应的编码输出（设编码器初始状态为0）。

（3）写出图中各点的码元速率，并画出各点的功率谱示意图。

解：（1）由图9-16可见，此卷积码编码器每输入1比特的a_j，就输出一个2比特的c_j1c_j2码字，且码字中的两个比特不仅与当前输入a_j有关，还与之前输入的两个信息比特a_j-1和a_j-2有关，关系为

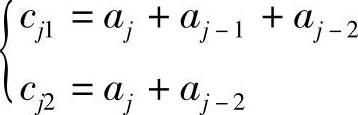
此关系即为卷积码的监督关系。

（2）根据上述监督关系，求出输入信息1100101时对应的编码器输出如表9-8所示。

表9-8 编码器输出

（3）A点为二进制单极性全占空矩形脉冲信号，其码元速率在数值上等于信息速率，为R_s=2MBaud，故功率谱密度如图9-17a所示。该卷积码编码器的编码效率为1/2，所以B点码元速率是A点码元速率的2倍，即为4MBaud，功率谱密度如图9-17b所示。C点的码元速率与B点相同，也是4MBaud，只是由单极性信号变成了双极性信号，因而功率谱密度中没有直流分量，功率谱密度如图9-17c所示。D点为16QAM调制信号，每个16QAM码元携带log₂M=log₂16=4bit信息，故D点信号的码元速率为1MBaud，又因为16QAM是调制信号，其功率谱的中心位置在载波频率处，主瓣宽度等于其码元速率的2倍，所以D点信号的功率谱如图9-17d所示。

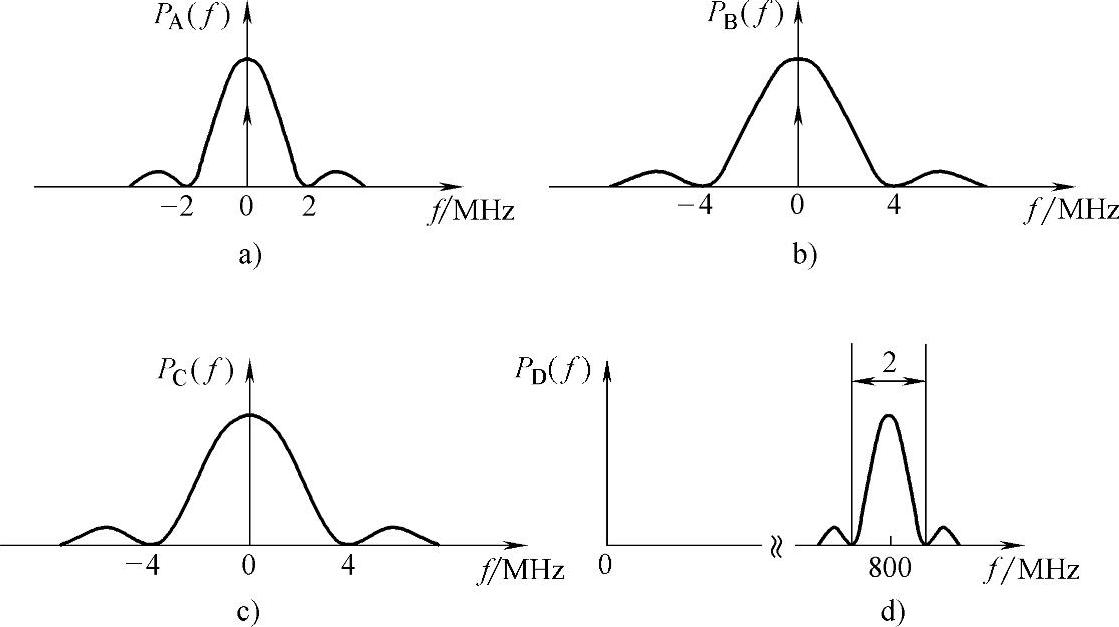
图9-17 各点信号功率谱示意图