1.设有一个码,它有三个码字,分别是(001010)、(111100)、(010001)。若此码用于检错,能检出几位错误?若此码用于纠错,能纠正几位错误?若此码同时用于纠错和检错,各能纠、检几位错误?
解:设三个码字分别表示为A0=[001010],A1=[111100],A2=[010001]。两两码字之间的距离为: d(A0,A1)=W(A0+A1)=4
d(A0,A2)=W(A0+A2)=4
d(A1,A2)=W(A1+A2)=4
显然,此码的最小码距d0=4。
(1)此码用于检错,能检测e≤(d0-1)=3位错误。
(2)此码用于纠错,能纠正t≤(d0-1)/2=1.5位错误,取整数,因此可纠一位错误。
(3)此码用于检错且纠错时,能检和能纠的个数e和t与最小码距之间应有如下关系:
d0≥e+t+1 (e>t)
可见,当d0=4时,有4≥2+1+1,得e=2,t=1。即同时用于检错和纠错时,纠一位错误的同时最多能检两位错误。
2.已知(7,3)线性分组码的生成矩阵为
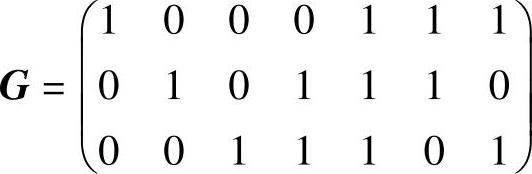
求:
(1)所有的码字。
(2)监督矩阵H。
(3)最小码距及纠、检错能力。
(4)编码效率。
解:(1)生成矩阵G有3行7列,可见k=3,n=7,r=n-k=7-3=4。
将信息矩阵M=[000]~[111]代入A=M·G即可求得所有码字为
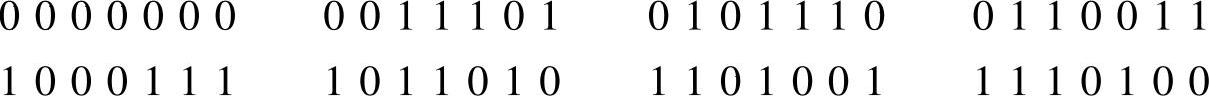
(2)由于G=[I3PT]=[IkPT]是一个典型生成矩阵,其中
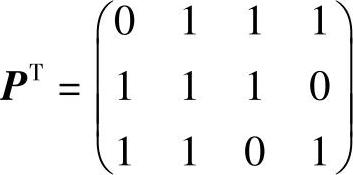 ,由此得到
,由此得到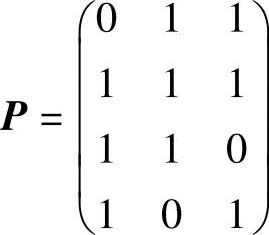
代入典型监督矩阵H=[PIr]=[PI4]求得
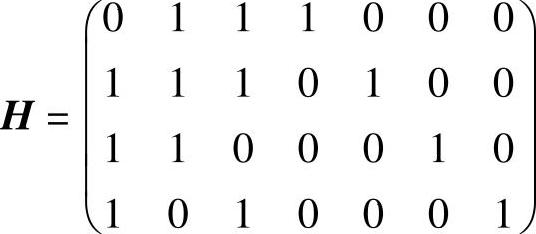
(3)码字集中除全0码字外,最小码字重量即为码的最小码距。可见,该码的最小码距d0=4。故此码若用于检错,最多能检测3位错误;若用于纠错,最多能纠正1位错误。
(4)编码效率为:η=k/n=3/7
3.对(7,1)重复码,求:
(1)全部码字。
(2)最小码距。
(3)用于纠错,最多能纠几位错误?
(4)用于检错,最多能检几位错误?
解:(1)(7,1)重复码的每个码字中有1个信息码元,6个监督码元,且每个监督码元与信息码元相同。故(7,1)重复码有两个码字,分别为0000000和1111111。
(2)两个码字之间的码距即为(7,1)重复码的最小码距,因此d0=7。
(3)此码用于检错,能检的错误数e≤d0-1=7-1=6。可见,最多能检6位错误。(4)此码用于纠错,能纠的错误数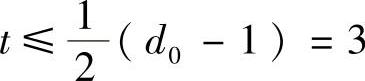 。可见,最多能纠正3位错误。
。可见,最多能纠正3位错误。
4.已知(7,3)分组码的监督关系式为
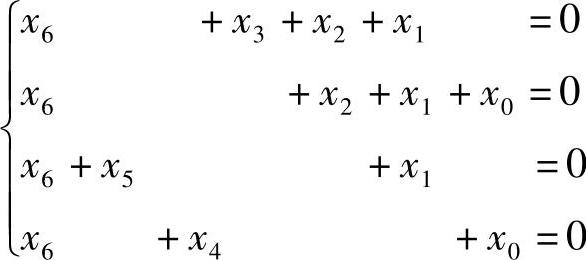
求其监督矩阵H、生成矩阵G、全部系统码字、纠错能力及编码效率η。
解:将监督方程组写成矩阵的形式
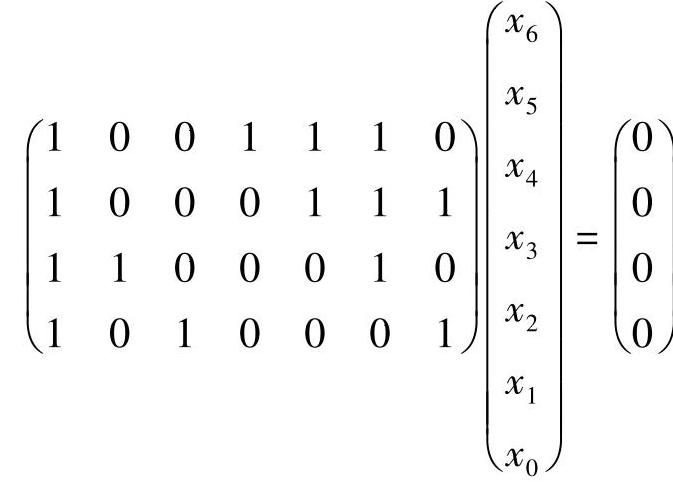
得监督矩阵为
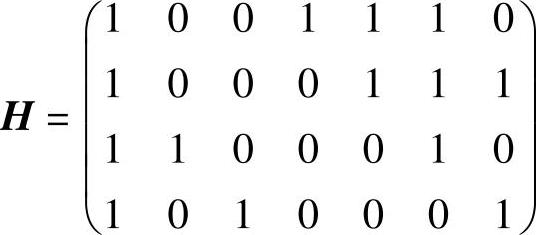
此矩阵不是典型监督矩阵,需将其转换为典型监督矩阵。首先将第3、4行加到第2行得
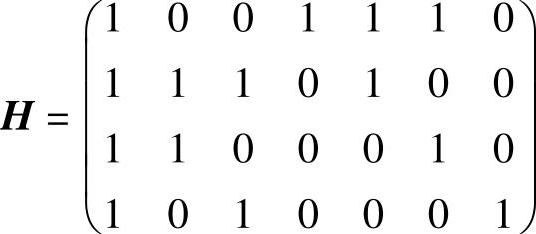
再将第2、3行加到第1行,得典型监督矩阵为
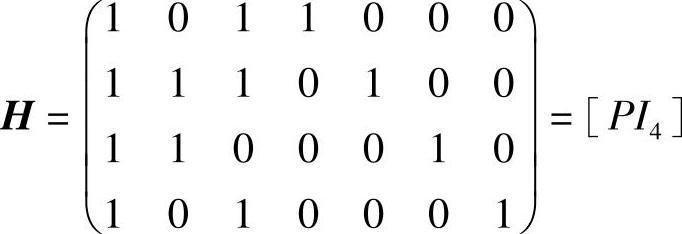
根据G=[I3PT]求得典型生成矩阵为
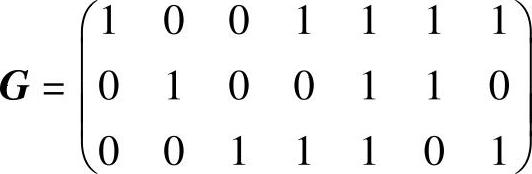
把由3位信息组成的信息矩阵逐个代入A=M·G,求得全部系统码字为

在线性分组码中,最小码距等于最小码重(除全0码字),即d0=minW(Ai)=3。代入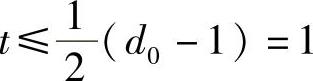 ,可见此码最多能纠一位错误。
,可见此码最多能纠一位错误。
编码效率为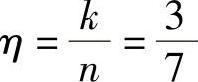
5.汉明码的监督矩阵为
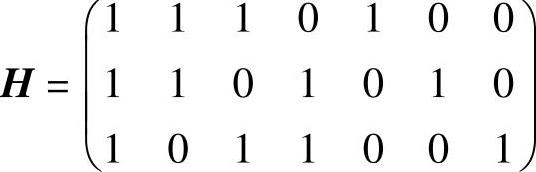
(1)求码长n和码字中的信息位数k。
(2)求编码效率η。
(3)求生成矩阵G。
(4)若信息位全为“1”,求监督码元。
(5)检验0100110和0000011是否为码字,若有错,请指出错误并加以纠正。
解:(1)监督矩阵H的行数等于监督元的个数,列数等于码字的长度。根据给定的监督矩阵可知n=7,r=3,k=7-3=4。
(2)编码效率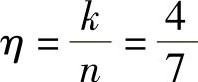 。
。
(3)此汉明码监督矩阵具有H=[PI3]形式,是典型监督矩阵,其中
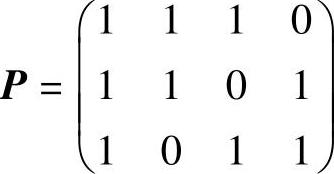
由此可得典型生成矩阵为
(4)当信息M=[1111]时,码字A=M·G=[1111111],可知监督码元(码字的最后3位)为111。
(5)当接收B=[0100110]时,由公式S=BHT求得其伴随式为
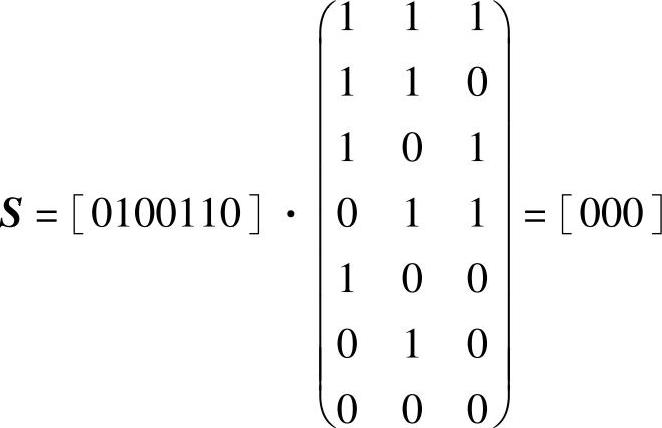
可见,接收码字B=[0100110]为此(7,4)汉明码的一个码字。
用同样的方法得到接收B=[0000011]的伴随式为(https://www.xing528.com)
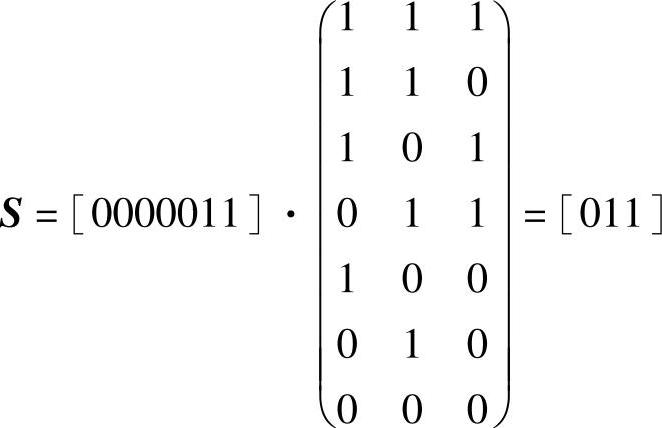
由于伴随式不为0,故B=[0000011]不是此(7,4)汉明码的一个码字,它是某个码字和错误图样的叠加。
要找出B=[0000011]中的错误,必须先找出所有单错误的7个错误图样与伴随式之间的关系。由S=EHT得伴随式与错误图样间的关系为
E1=[1000000]⇒S=[111]
E2=[0100000]⇒S=[110]
E3=[0010000]⇒S=[101]
E4=[0001000]⇒S=[011]
E5=[0000100]⇒S=[100]
E6=[0000010]⇒S=[010]
E7=[0000001]⇒S=[001]
由此可见,S=[011]对应的错误图样为E4=[0001000],即接收码字B=[0000011]中第4位(从左起)有错。纠错后的码字为A=B+E4=[0000011]+[0001000]=[0001011]。
6.一码长n=7的汉明码,监督位数r为多少?信息位数k为多少?编码效率η为多少?试设定一种伴随式与错误图样的对照表并写出监督码元与信息码元之间的关系式。
解:汉明码的监督码元个数r与码长n之间满足
n=2r-1
由n=7得r=3,信息元个数k=n-r=7-3=4。
编码效率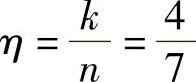 。
。
要求监督关系方程组,必须先求出监督矩阵H。由于HT中的每一行都是一个伴随式,第一行对应错误图样E1=[1000000],第二行对应错误图样E2=[0100000],以此类推。(7,4)汉明码的监督矩阵H有3行7列,因此HT有3列7行,每一行由3位二进制码元构成。3位二进制码元不同的组合共有8种,去掉000,其余7种与7个错误图样的伴随式对应,它们之间的各种一一对应关系都可以。但我们可选择一种能导出典型监督矩阵的对应关系,即错误图样E5=[0000100]对应S=[100],E6=[0000010]对应S=[010],E7=[0000001]对应S=[001],其余E1~E4与[111]、[110]、[101]、[011]之间可任意对应。可选择如下的对应关系:
E1=[1000000]⇒S=[110]
E2=[0100000]⇒S=[101]
E3=[0010000]⇒S=[111]
E4=[0001000]⇒S=[011]
E5=[0000100]⇒S=[100]
E6=[0000010]⇒S=[010]
E7=[0000001]⇒S=[001]
于是有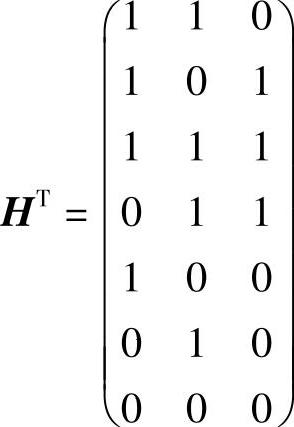
所以 根据监督矩阵H及式H·AT=OT得
根据监督矩阵H及式H·AT=OT得
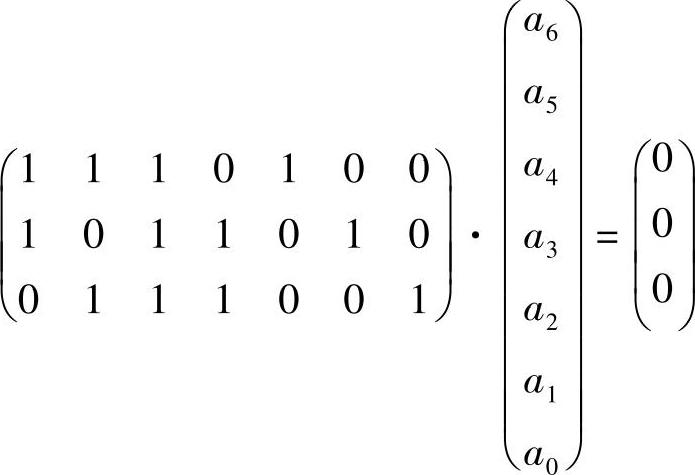
即有监督方程组
a6+a5+a4+a2=0
a6+a4+a3+a1=0
a5+a4+a3+a0=0
整理后得监督元与信息元之间的关系式为
a2=a6+a5+a4
a1=a6+a4+a3
a0=a5+a4+a3
7.已知(7,4)循环码的生成多项式g(x)=x3+x+1。
(1)画出编码电路。
(2)列出输入信息为“1100”时的编码过程表(设初始状态为0)。
(3)画出此循环码的译码电路。
解:(1)根据给定生成多项式及图9-3,画出此(7,4)循环码编码电路如图9-11所示。
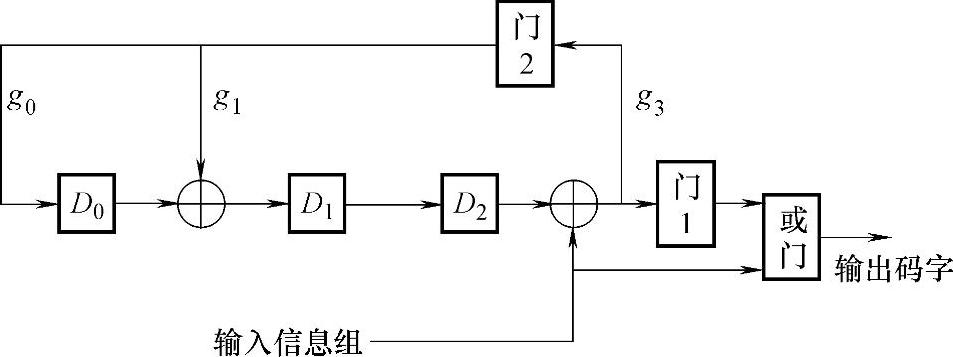
图9-11 (7,4)循环码编码电路
(2)根据移位寄存器的工作原理,当输入信息为1100时,编码器的工作过程如表9-5所示。
(3)最高位发生错误时的错误图样多项式为e(x)=x6,对应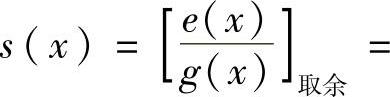
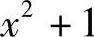 ,得
,得
表9-5 编码器工作过程

D2D1D0=101,即可由D2、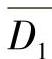 、D0相与得到纠错信号。故循环码译码器的原理图如图9-12所示。
、D0相与得到纠错信号。故循环码译码器的原理图如图9-12所示。
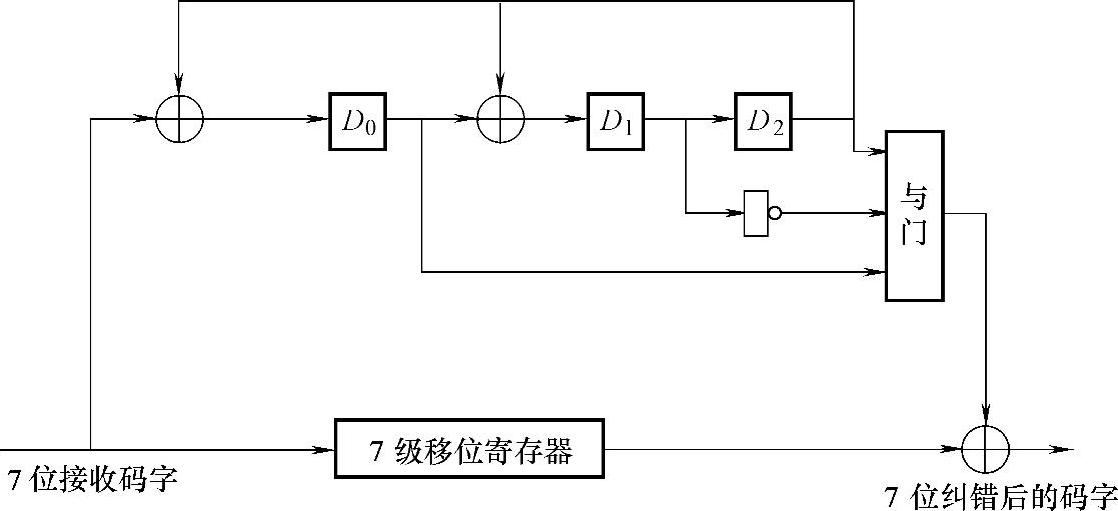
图9-12 (7,4)循环码译码器电路
8.试构成周期长度为7的m序列发生器,并求出相应的m序列。
解:根据x7+1=(x+1)(x3+x+1)(x3+x2+1)及特征多项式条件,可以验证f(x)=x3+x+1和f(x)=x3+x2+1都是产生长度为7的m序列的本原特征多项式。
(1)用f(x)=x3+x+1画出的m序列发生器框图如图9-13所示。
(2)当初始状态a2a1a0=001时,输出m序列为1001110。产生过程如表9-6所示。
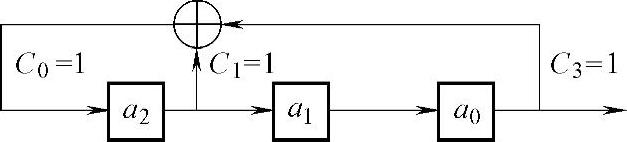
图9-13 m序列发生器
表9-6 m序列产生过程

(续)

9.有卷积编码器如图9-14所示。求当输入信息序列为“1100100011”时的编码器输出的码字序列。
解:设寄存器中的初始值为0。由编码器可见,每输入一位信息aj,输出码字有两位aj1aj2,其中aj1=aj⊕aj-1,aj2=aj。编码器工作过程如表9-7所示。
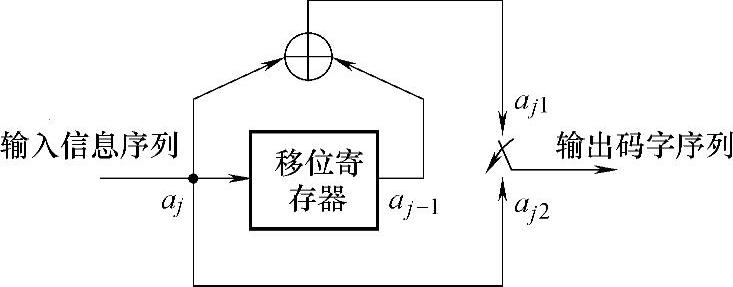
图9-14 卷积码编码器
表9-7 卷积码编码器工作过程
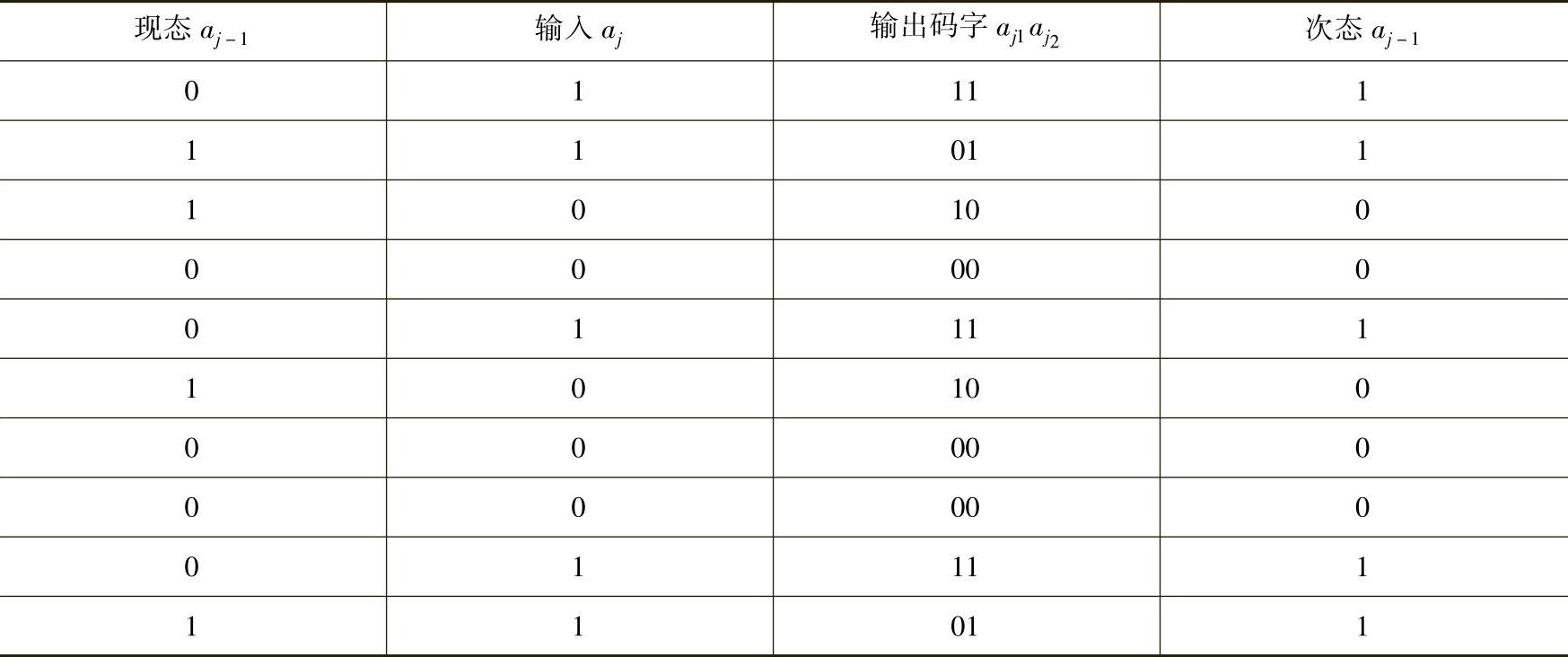
由表9-8可见,当输入信息为1100100011时,输出码字序列为:11,01,10,00,11,10,00,00,11,01。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




