构造周期为15的m序列产生器及其性质

m序列是由线性反馈移位寄存器产生的周期最长的码序列，具有类似于随机序列的一些统计特性，所以称为伪随机序列（也称PN码）。

1.m序列的产生

n级线性反馈移位寄存器的一般结构如图9-8所示，它能产生周期为P≤2ⁿ-1的码序列。若P=2ⁿ-1，则为m序列。

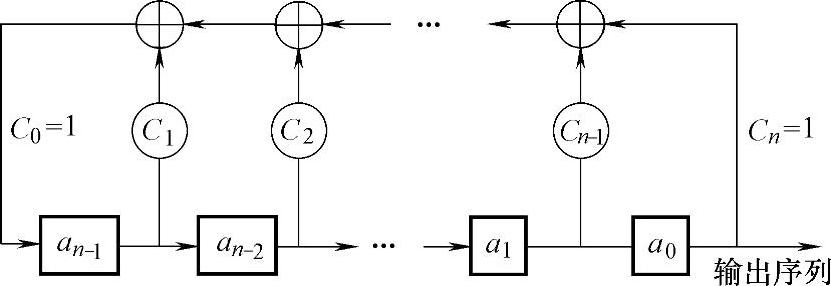
图9-8 n级线性反馈移位寄存器

图9-8所示线性移位寄存器的反馈连接状态可用多项式表示

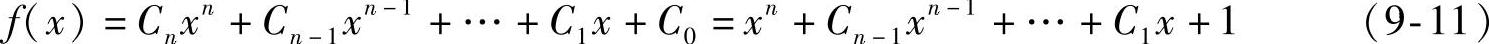
称为线性反馈移位寄存器的特征多项式。其中C_i=1或0分别表示对应反馈线的有无。

可以证明，一个n级线性反馈移位寄存器产生m序列的充要条件是：其特征多项式f（x）为一个n次本原多项式，即满足如下条件：

1）f（x）为既约多项式（不可再分解）。

2）f（x）能整除x^P+1，即f（x）是x^P+1的因子，其中P=2ⁿ-1。

3）f（x）不能整除x^q+1，其中q<P。

根据上述三个条件可求得本原多项式f（x），由本原多项式就可画出m序列产生器。

例如，当n=4时，有P=15，因式分解如下

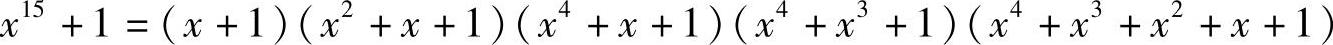
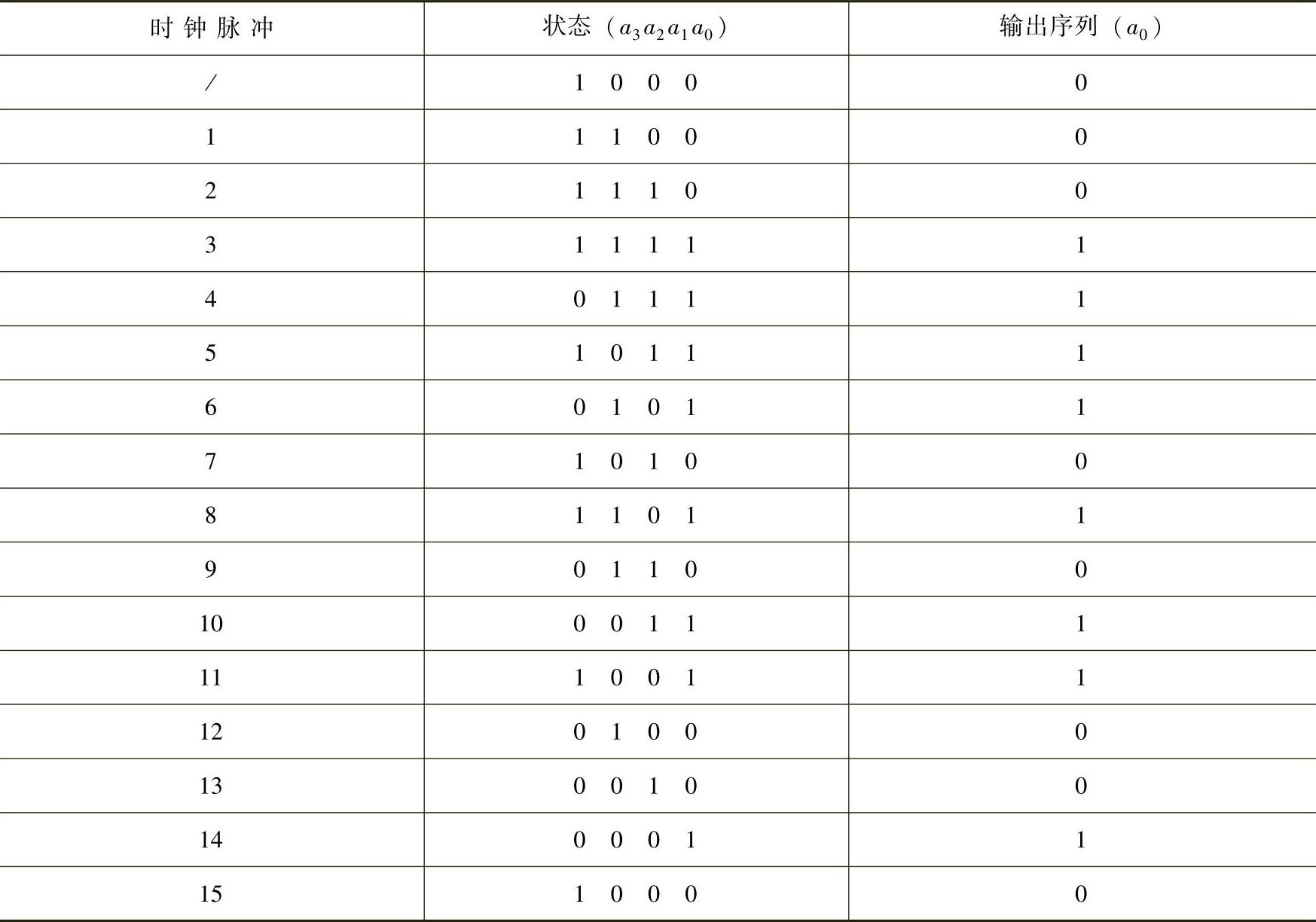
其中4次既约多项式有三个，但x⁴+x³+x²+x+1能整除x⁵+1，不是本原多项式。可以验证，x⁴+x+1和x⁴+x³+1都是本原多项式，利用任意一个都可以构造出周期为15的m序列产生器。f（x）=x⁴+x+1对应的m序列产生器如图9-9所示。若初始状态为a₃a₂a₁a₀=1000（非全0即可），则电路经过15个时钟后回到状态1000，输出序列的周期为15。电路状态的变化及相应的输出序列如表9-4所示。

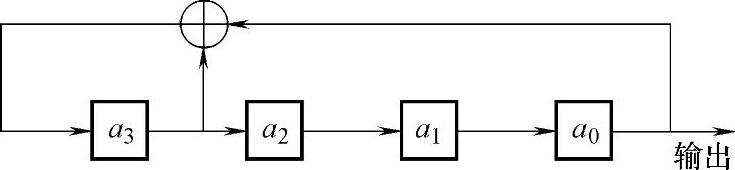
图9-9 周期为15的m序列产生器

表9-4 图9-6电路状态变化及输出序列

2.m序列的性质(www.xing528.com)

（1）均衡性

每一周期内，“1”的个数比“0”的个数多1个，即“1”、“0”个数近似相等。

（2）游程特性

游程是指序列中连续出现的同种码元。如序列1011000中，共有4个游程，分别为“1”、“0”、“11”、“000”。游程中的码元数目称为游程长度，如游程“000”的长度为3。

m序列每个周期中长度为k的游程个数为2^n-k-1。一个周期中的游程总数为2^n-1，其中“0”游程和“1”游程各占一半。

（3）移位相加特性

一个m序列与其任意次移位后的序列相加（对应位异或），其结果仍为m序列，且是原m序列某次移位后的序列。如表9-4中的m序列与其延迟2位后的序列相加，结果为原序列延迟8位后的m序列，即

000111101011001，00011…（原m序列）+010001111010110，01000…（延迟2位后的m序列）=010110010001111，01011…（延迟8位后的m序列）

（4）自相关特性

周期为P的m序列一个周期内的自相关函数为

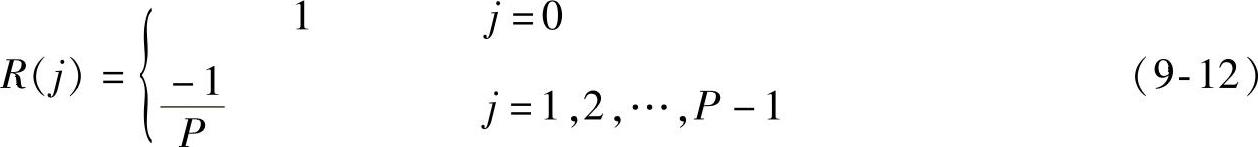
容易验证，R（j）是偶函数，R（j）是周期函数，示意图如图9-10所示。

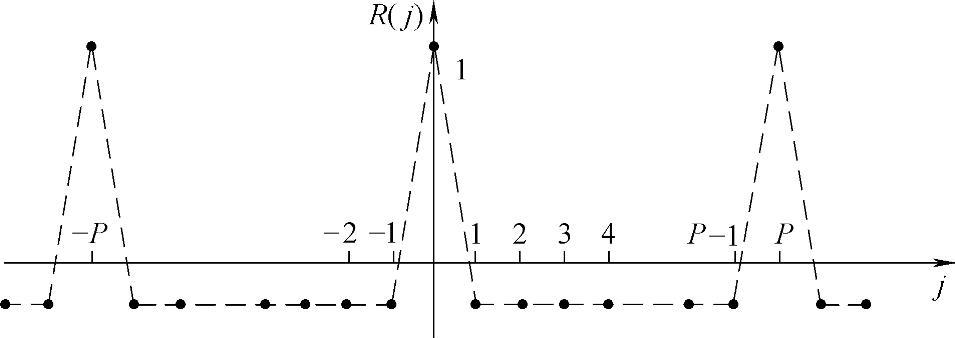
图9-10 m序列的自相关函数

（5）伪噪声特性

若对白噪声取样，当样值大于0时，判为“1”码元，反之，判为“0”码元，这样就可得到一个由“1”、“0”组成的码元序列，这个码元序列即为噪声序列。其特点如下：

1）“1”、“0”等概。

2）长度为k的游程总数约占游程总数的1/2^k，且“1”、“0”游程的数目各占一半。

3）功率谱为n₀/2的白噪声的自相关函数为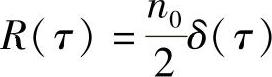，是个冲激函数。

上述（1）～（4）性质表明，m序列与噪声序列十分相似，故称m序列为伪噪声序列。由于m序列便于产生，故在通信、测距等领域得到广泛应用。