线性分组码第二种方法介绍：以（7，3）码为例

1.特点

1）既是线性码又是分组码。因此，一个码字中的监督码元只与本码字中的信息码元有关，而且这种关系可以用线性方程来表示。如某（7，3）线性分组码，码字a₆a₅a₄a₃a₂a₁a₀中前3位表示信息码元，后4位表示监督码元，监督码元与信息码元之间的关系为：

式中，“+”为“异或”或模2运算。

式（9-1）的方程组又称为监督关系。若给定信息码元，即可求出相应的监督码元，将监督码元附加在信息码元后即可得到一个码字。例如，当信息码元a₆a₅a₄=111时，代入上式求得监督码元a₃a₂a₁a₀=0100，得到码字为1110100。显然，每一组信息码元对应一个码字，故（7，3）线性分组码共有8个码字。一般地，线性分组码（n，k）共有2^k个码字。编码器的工作就是根据输入的信息码元及预先设计好的监督关系计算监督码元，然后输出码字。

2）具有封闭性。即码字集中任意两个码字之和（对应位异或）仍然是码字集中的一个码字，因而最小码距等于非全0码字的最小重量。

3）存在全0码字。当信息码元为全0时，代入监督关系求得监督码元全为0。

2.线性分组码的编码

编码就是求码字。当信息码元和监督关系给定时，求码字的方法主要有两种：①将信息码元代入监督关系求得监督码元，将监督码元附加在信息码元后即得到码字，如上例。②用信息矩阵乘以生成矩阵。下面仍以式（9-1）所示的线性分组码为例介绍第二种方法。

将式（9-1）所示的监督关系改写为

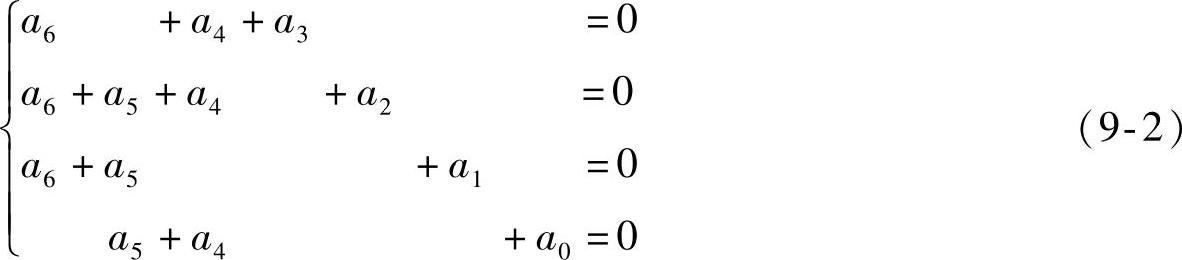
将这组线性方程组写成矩阵形式

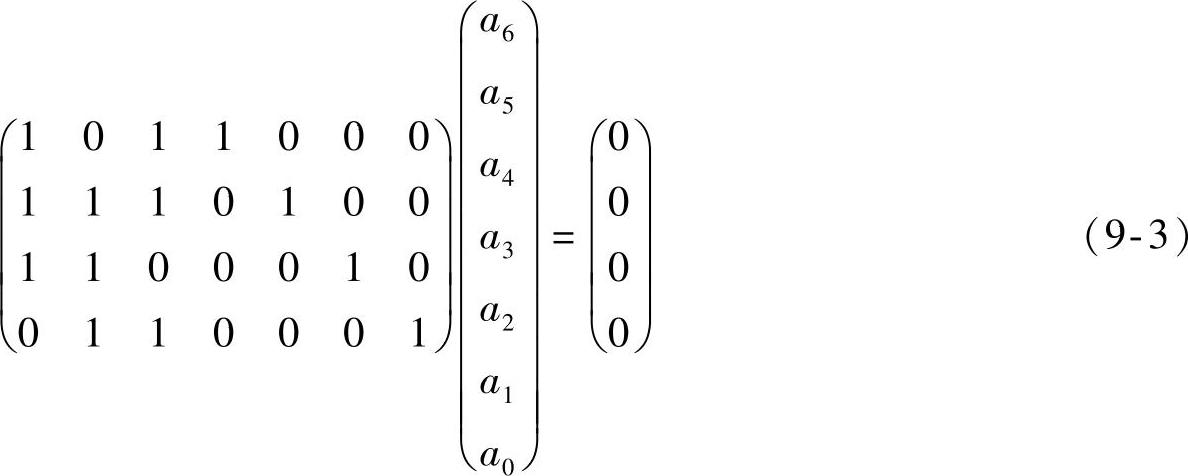
并简记为 H·A^T=O^T 或 A·H^T=O （9-4）

式中，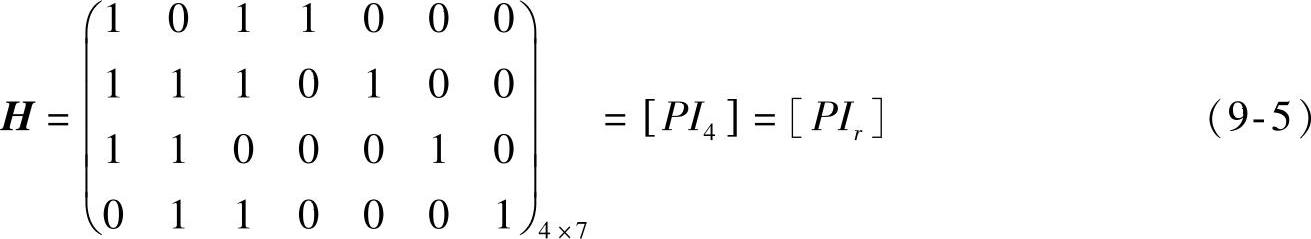

A=[a₆a₅a₄a₃a₂a₁a₀]

O=[0 0 0 0]

H称为监督矩阵，它是一个r×n矩阵；A为码字矩阵；I_r为r×r阶单位矩阵。

具有H=[PI_r]形式的监督矩阵称为典型监督矩阵。由典型监督矩阵H可求得典型生成矩阵G

G=[I_kP^T] （9-6）

式中，I_k为k×k阶单位矩阵；k为码字中的信息码元个数。可见，G是一个k×n阶矩阵。

如式（9-5）中H对应的生成矩阵为

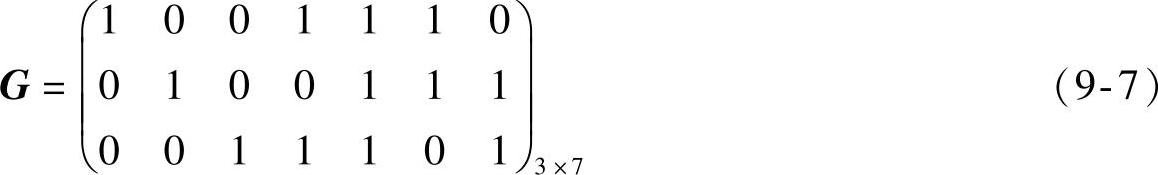
用生成矩阵G可求得所有码字，方法为

A=M·G （9-8）

式中，M为信息码元矩阵。如当信息码元a₆a₅a₄=111时，M=[111]，用式（9-8）得到A=[1110100]，与用式（9-1）监督关系求得的码字相同。改变信息码元矩阵M，可求得其余的7种码字。通过计算可以发现，任一码字A都是G的各行的线性组合，且G的各行本身就是一个码字。

注意：●由典型矩阵G生成的线性分组码为系统码。

●非典型形式的H、G可以经过行线性变换转换成典型矩阵。

3.线性分组码的译码

译码就是对接收码字进行检错和纠错。

（1）错误图样E

设发送码字A=[a_n-1a_n-2…a₁a₀]，接收码字B=[b_n-1b_n-2…b₁b₀]，定义错误图样

E=[e_n-1e_n-2…e₁e₀]

式中，即e_i=0，表示接收码字的第i位无错；e_i=1表示第i位有错。例如，若发送码字A=[1001110]，接收码字B=[1001100]，则错误图样E=[0000010]，表示b₁位有错。

根据错误图样的定义，有B=A+E和A=B+E。

（2）伴随式S与错误图样E的关系

定义伴随式S=BH^T。由B=A+E及式（9-4）得

S=（A+E）·H^T=A·H^T+E·H^T=E·H^T

可见，S仅与错误图样E有关，而与发送码字无关。这说明，计算接收码字的伴随式可获知接收码字的错误图样，知道了错误图样就可以纠错了。因此，译码开始前需要将错误图样与伴随式之间的关系存于译码器中以备查用。若监督矩阵为式（9-5）所示，则S与部分E（无错和单个错）之间的对应关系如表9-1所示。

表9-1 伴随式S与错误图样E的对应关系

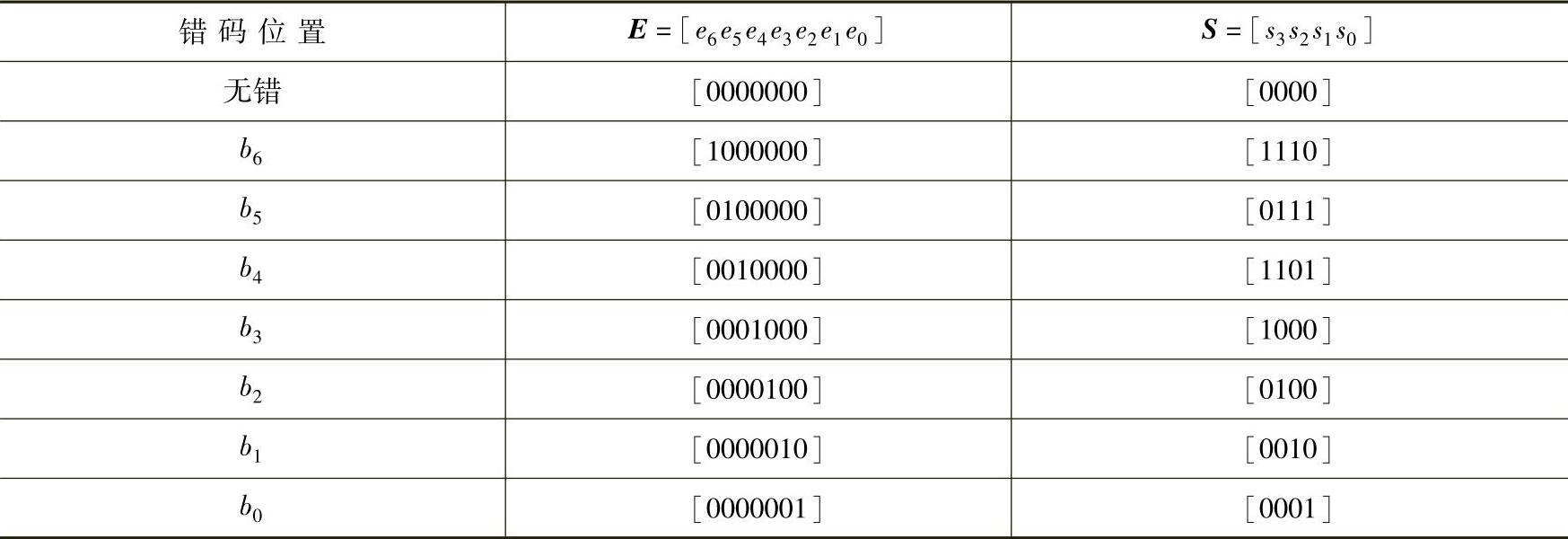
从表9-1可看出，接收码字无错时，伴随式是1行r列的全0矩阵，而7个单错误图样的伴随式S则各对应H^T中的一行。

（3）译码步骤

1）对接收码字B计算伴随式：S=BH^T。

2）若S=0（全0矩阵），表示接收码字无错。

3）若S≠0，则由S查表得错误图样E，将E和接收码字B相加（对应位异或）得到纠错后的码字A=B+E。（注：若仅检错，则无需纠错，要等待发送端重传）

例如，接收码字B=[1000000]，则S=BH^T=[1110]，查表9-1得E=[1000000]，则纠错后的码字A=B+E=[1000000]+[1000000]=[0000000]。

特别强调：

●当码字中的错误个数超出码的纠错能力时，会发生越纠越错现象。如当发送码字为A=[0100111]，假如传输过程中发生3个错误，错误图样为E=[0000111]，则接收码字为B=[0100000]。译码器计算此接收码字的伴随式，得S=BH^T=[0111]，查表得E=[0100000]，译码器认为b₅发生错误，因此纠错后的码字为[0000000]。可见，纠错后码字中有4位错误。

●若一个码字在传输过程中错成了另一个码字，则译码器将无法发现错误。如发送码字A=[0100111]，若错4位后为B=[0111010]，计算伴随式得S=0，译码器认为接收码字中没有错误。

这些情况的发生都是因为码字中的错误个数超出了码的纠错能力（如（7，3）分组码最小码距为4，能纠正一位错误）。因此，在设计信道编码方案时，应充分考虑信道发生错误的情况，选择纠检错能力合适的纠检错码。

4.汉明码

汉明码是能够纠正一位错误、编码效率最高的线性分组码。具有如下特点：

1）最小码距d₀=3。(www.xing528.com)

2）码长n与监督码元数r间有如下关系：n=2^r-1，且r≥3。

当r=3、4、5…时，分别为（7，4）（15，11）（31，26）汉明码等。

5.循环码

循环码是线性分组码的另一个重要子集。它具有线性分组码的一切性质，此外还具有循环移位特性。所谓循环移位特性是指码字集中任一码字循环移位后仍为码字集中的一个码字。例如，表9-2所示的（7，3）循环码中，任一码字，设1010011，其最右边的一位码元移位到最左边（或反之）后仍为其中的一个码字1101001。

表9-2 （7，3）循环码

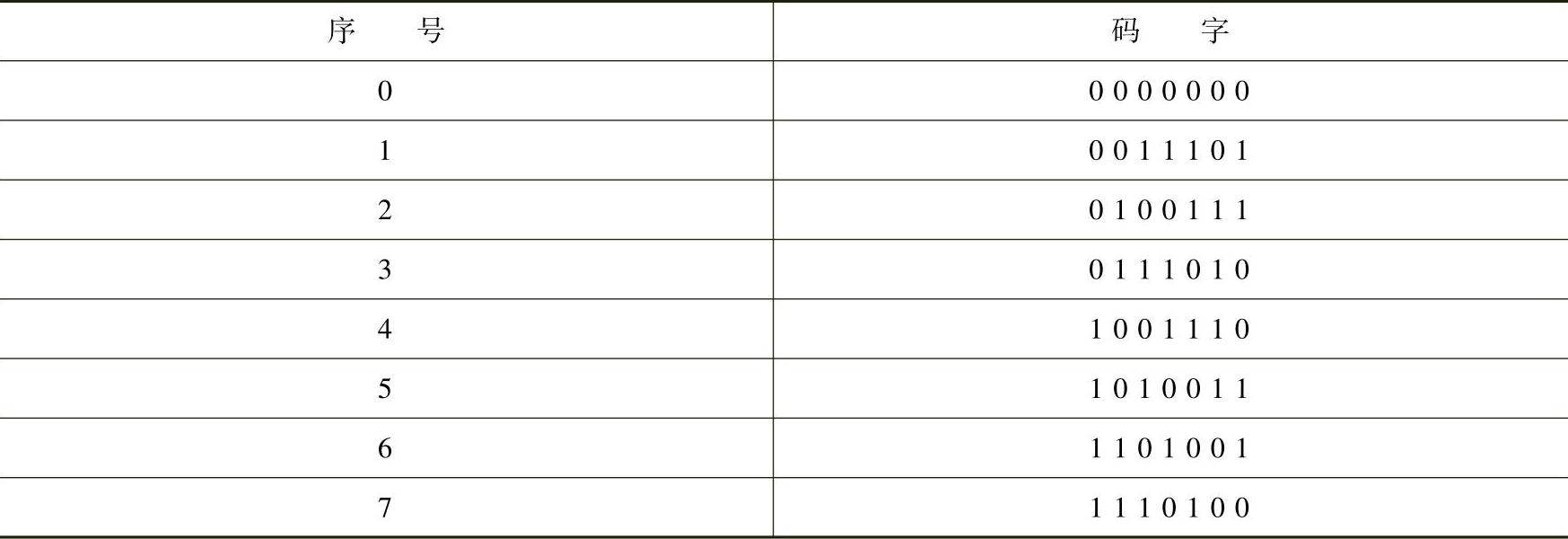
（1）码字多项式

码字A=[a_n-1a_n-2…a₁a₀]多项式的一般形式为

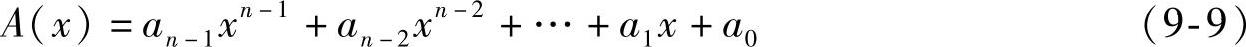
如码字A=[1001110]，其多项式为A（x）=x⁶+x³+x²+x。需要注意的是，由码字多项式写出码字时应根据码字长度补足位数（高位补0）。

（2）循环码的编码

循环码的编码基于生成多项式g（x）。

（n，k）循环码的g（x）具有如下特性。

1）g（x）是xⁿ+1的因式。

2）g（x）是r=n-k次多项式。

3）g（x）的常数项为1。

4）g（x）是次数最低的码字多项式（全0码字除外）。

利用前三项特性可寻找（n，k）循环码的生成多项式g（x）。以（7，3）循环码为例，首先对x⁷+1进行因式分解（可查表），得到

x⁷+1=（x+1）（x³+x+1）（x³+x²+1）

然后找到次数为r=7-3=4、常数项为1的因式即为生成多项式。本例中有x⁴+x³+x²+1（第一项和第二项相乘）和x⁴+x²+x+1（第一项和第三项相乘）两个生成多项式，前者生成表9-2所示的（7，3）循环码。

也可利用最后一项特性从码字集得到生成多项式g（x）。例如，由表9-2所示码字得到该循环码的生成多项式为g（x）=x⁴+x³+x²+1（对应码字0011101）。

有了生成多项式g（x）即可进行循环码的编码。编码方法有两种：

1）线性分组码方法，即A=M·G。

由生成多项式构造生成矩阵G的方法如下：

将每行多项式写成码字形式得生成矩阵G，但它通常不是典型生成矩阵。因此，要想得到系统码，需将其转化为典型生成矩阵。

例如，当g（x）=x⁴+x³+x²+1时，对于（7，3）循环码有

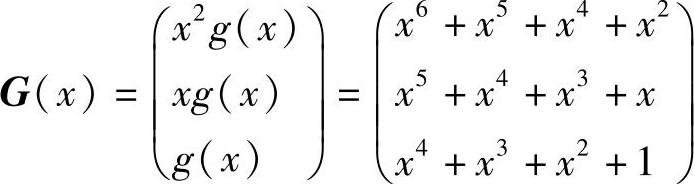
将各行多项式写成码字，再做适当的行运算，得到典型生成矩阵为

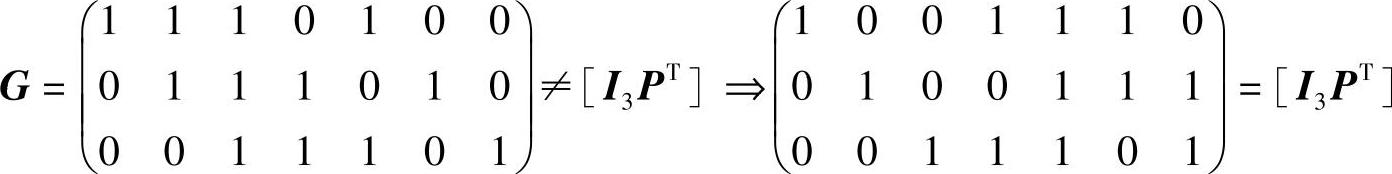
2）用循环码特有方法：即A（x）=x^n-kM（x）+[x^n-kM（x）]′，其中[ ]′为除以g（x）取余。

以上述（7，3）循环码为例，g（x）=x⁴+x³+x²+1，若信息M=[110]，则M（x）=x²+x，x^n-kM（x）=x⁴（x²+x）=x⁶+x⁵，[x⁶+x⁵]′的求解过程如下^[1]：

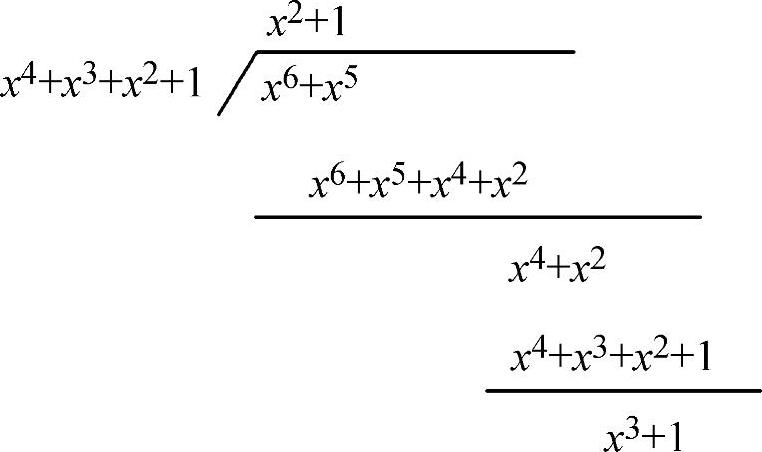
求得余式为[x⁶+x⁵]′=x³+1，故得到码字多项式为

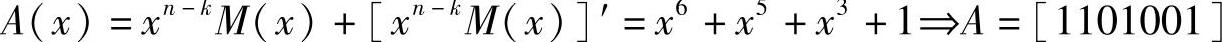
由上可见，A（x）=x^n-kM（x）+[x^n-kM（x）]′中的前一项表示信息码元放置于码字左端，后一项对应监督码元。

这种编码方法可用r=n-k级移位寄存器实现。多项式为g（x）=x^r+g_r-1x^r-1+…+g₁x+1的（n，k）循环码的编码电路如图9-3所示。若g_i=1，则对应的反馈线连通，否则断开。

编码过程：

●初始状态清零，门1断开，门2接通。信息码元（m_k-1m_k-2...m₁m₀）一方面在时钟脉冲的控制下依次进入编码器（m_k-1首先进入）计算监督码元，另一方面经或门直接输出。

●一旦信息码元全部输入到编码器，移位寄存器中的内容即为本组信息的监督码元。这时，门2断开，门1接通，在时钟的控制下将移位寄存器中的监督码元依次输出，这些监督码元和前面输出的信息码元组成一个码字。

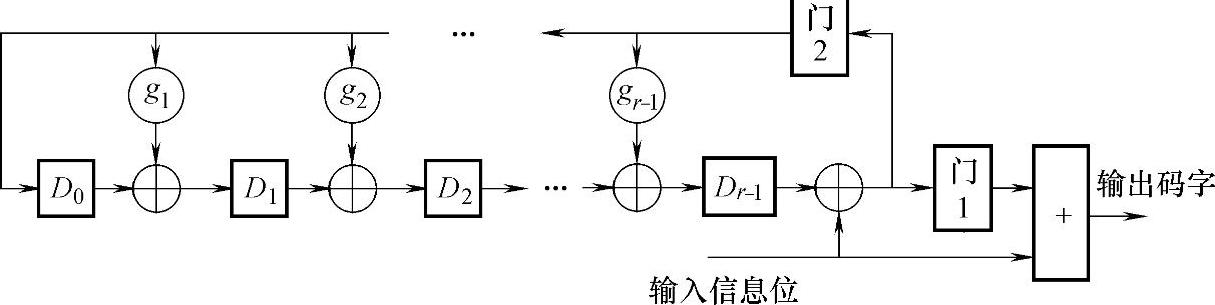
图9-3 用移位寄存器实现的循环码编码器

（3）循环码的译码

译码的目的是对接收码字检错和纠错。步骤如下：

1）用式S（x）=[e（x）]′可计算出伴随多项式S（x）与错误图样多项式e（x）之间的关系，将此关系预先存于译码器中。表9-3是（7，3）循环码的S（x）与e（x）间的关系（g（x）=x⁴+x³+x²+1）。

2）当接收到码字时，计算S（x）=[B（x）]′。

3）若S（x）=0，则接收码字无错；若S（x）≠0，则由S（x）查表求得错误图样多项式e（x），并对接收码字进行纠错，即A（x）=B（x）+e（x）。

表9-3 （7，3）循环码伴随多项式与错误图样多项式间的关系

循环码的译码也可用r=n-k级移位寄存器实现。生成多项式为g（x）=x⁴+x³+x²+1的（7，3）循环码的译码器如图9-4所示，最上部分是移位寄存器，其反馈线的连接与生成多项式的系数一致，它完成伴随式的计算。中间部分的非门和与门的连接方式则由最高位发生错误时的伴随式确定，它确定错误图样并由此产生纠错信号。下半部分缓冲寄存器和异或门完成对接收码字的纠错。

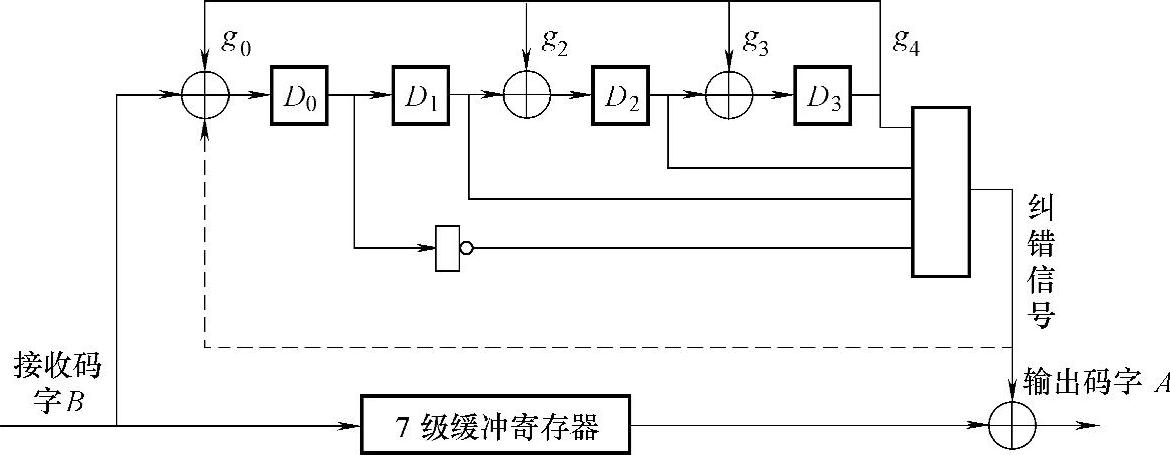
图9-4 （7，3）循环码译码器

需要指出的是，循环码是线性分组码，故它也可以采用线性分组码的译码方法。此外，各种编译码算法不仅可以用硬件实现，也可以用软件编程来实现。